MRD:01336581

Excercise 1

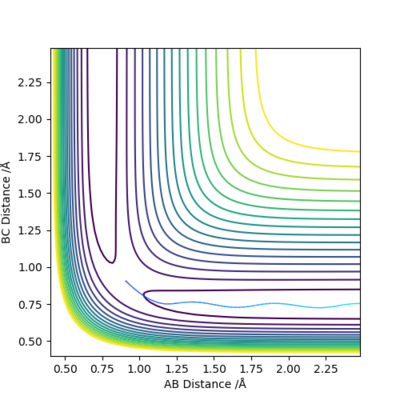
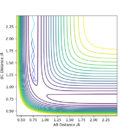
The reaction transition state happens at a saddle point on the energy surface.

$\frac{\partial V}{r_{1}} = \frac{\partial V}{r_{2}} = 0$

$\frac{\partial^{2} V}{r_{1}^{2}}$ and $\frac{\partial^{2} V}{r_{1}^{2}}$ are of opposite sign.

Good, but you need to explain what do those two maths functions mean. Why the first derivatives are zero and the second derivatives are opposite signs ? Do your r1, r2 represent the two distances AB and BC? if so, I'm afraid it is not really correct. Sw2711 (talk) 14:32, 3 June 2019 (BST)

The transition state is located between r_ts = 0.907742 Å and 0.907743 Å. How did you find the values? Sw2711 (talk) 14:32, 3 June 2019 (BST)

The dynamics simulation differs from the MEP simulation by showing the vibration of the product molecule. Okay, why is it? Is it the only difference you've observed? Sw2711 (talk) 14:32, 3 June 2019 (BST)

For the initial conditions r₁ = 0.74 and r₂ = 2.0

p₁	p₂	E_tot	Reactive?	Description of the dynamics
-1.25	-2.5	-99.018	Yes	Approaches transtition state smoothly. The product molecule has a small vibrational energy.
-1.5	-2.0	-100.456	No	Reactant molecule has a small vibrational energy. It does not pass over the transition state and does not react.
-1.5	-2.5	-98.956	Yes	Reactant molecule has a small vibrational energy. It passes over the transiton state, and the product molecule has a slightly larger vibrational energy.
-2.5	-5.0	-84.956	No	The reactants approach the transition state quickly, and pass over. They gain a large vibrationl energy, and the products vibrate back into the reactants. the reactant molecule is left with a large vibrational energy.
-2.5	-5.2	-83.416	Yes	The reqactants approach each other quickly, and pass through the transition state, gaining a large vibrational energy. they vibrate back over the transition state,towards the reactants, and then back ovetr the tranition state again, leaving the product molecule with a large vibrational energy.

Transition state theory assumes that the reaction passes over the lowest energy point on the energy surface, i.e. the saddle point. This does not always happen if the reactants have higher energies. This can lead to recrossing the transition state. If the tranisiton state is recrossed, any rate calulations are unlikely to be accurate, since the time for the reaction to complete is longer than if the transition state was not recrossed. The transition state theory rate predictions form an upper bound for the rate constant.

This part is good. But you need to be aware that there are a few more assumptions in TST. Sw2711 (talk) 14:32, 3 June 2019 (BST)

Excercise 2

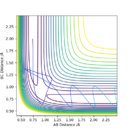
The potential energy surface shows that the reaction of F with H₂ is exothermic, and the reaction of HF with H is endothermic.

For this simulation the F atom is in positoin A, so the left hand side is the F + H₂, and the right hand side is the HF + H side. the left hand side is higher in energy, so going from F + H₂ to HF + H is exothermic. This shows that the H-F bond is stronger than the H-H bond, since overall energy is released on the formation of the H-F bond over the H-H bond.

This part is good. Sw2711 (talk) 14:37, 3 June 2019 (BST)

The transition state is approximately at F-H = 1.81 Å and H-H = 0.745 Å.

You need to explain your approach.Sw2711 (talk) 14:37, 3 June 2019 (BST)

A minimum energy pathway from these values gave a value for the activation energy of the HF + H reaction of 30 kcalmol^-1.

A minimum energy pathway calculated from F-H = 1.82 Å and H-H = 0.745 Å resulted in a value for the activation energy of ~0.25 kcalmol^-1.

This part is goodSw2711 (talk) 14:37, 3 June 2019 (BST)

A reactive pathway has initial conditions r_FH = 2 Å, r_HH = 0.74 Å, p_FH = -0.8, p_HH = 0.

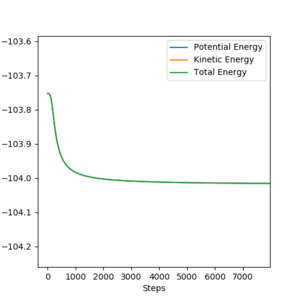
The reaction energy is released by the formation of the H-F bond. Quantum mechanically, the constructive overlap of electron wavefunctions is stabilising, which releases energy to be converted into vibrational or translational forms. This can be shown by removing the fluorine atom, leaving just the atomisation of a hydrogen molecule, which is endothermic. Okay, so, 1. how do you see the energy is conserved in your program. 2. in reality, what kind of technique you need to do, to remove the fluorine atom, according to what you said? Sw2711 (talk) 14:37, 3 June 2019 (BST)

Polanyi's rules state that vibrational energy is more useful for promoting reactions with a late transition state, and translational energy is more useful in promoting reactions with an early transition state. For the reaction between HF and H, the transition state is very late, so a small amount of energy in the vibration of the HF molecule results in a reaction, whereas a much larger amount of translational energy on the H atom results in an unreactive pathway. The inverse is true for the reaction between F and H₂.

If you have tested using HF+H system, you need to show me. Sw2711 (talk) 14:39, 3 June 2019 (BST)