MRD:01330404

Molecular Reaction Dynamics

Objectives

The objectives of this wiki report is to provide a study on triatomic system reactivities, which involves the collision between one atom and a diatomic molecule.

---

Transition states

Figure 1. A potential energy surface diagram. The saddle point indicates the transition state.

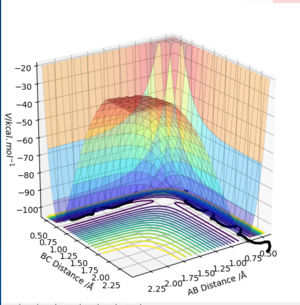
A transition state is the saddle point on a potential energy surface diagram.

Elegant definition, as 'saddle point' already includes the gradient to be zero. However, if you want to be picky, then you have to also specify that the saddle point is of first order, i.e. there is one and exactly one negative component of the hessian. See also the first year gaussian labsFdp18 (talk) 09:03, 4 May 2019 (BST)

Suppose a function f(x,y) with two variables x and y. At a stationary point (x₀,y₀), the first order partial derivatives of f(x,y) (noted ∂f/∂x and ∂f/∂y, or f_x and f_y) both equal to zero.

The second order derivatives are noted as f_xx and f_yy.

For a stationary point where f_x = 0 and f_y = 0, it is a saddle point if it satisfies the following:

(f_xxf_yy - f_xy ²) < 0

That appears to be correct - you are using the determinant to test for definiteness together with Schwarz's theorem. This will give you, however, any saddle point for a general problem. It is entirely acceptable to just consider the eigenvalues of the Hessian without saying how you obtain them - you are studying chemistry and not maths.Fdp18 (talk) 09:14, 4 May 2019 (BST)

where f_xy is firstly taken from the partial derivative of f(x,y) with respect to x and then take its partial derivative with respect to y.

A local minimum satisfies the following:

(f_xxf_yy - f_xy ²) > 0 and f_xx > 0

A minimum point in a potential energy surface diagram refers to a stable or quasi-stable species, e.g. reactants or products.

Although all that is sort of correct (apart from the too general saddle point definition), you should include proper references so I can check that you did not just copy something without understanding what it means.Fdp18 (talk) 09:14, 4 May 2019 (BST)

---

Transition state position

The best estimation of the transition state (r_ts) obtained from calculation is 0.9077. The imported values are r₁ = r₂ = 1.2 Å, and p₁ = p₂ = 0. The potential energy surface data are exported and the value from the last calculation (step number 1000) is the one closest possible to the true value at the transition state (the saddle).

I assume by 'calculation' you mean a MEP, which you should state somewhere.Fdp18 (talk) 09:19, 4 May 2019 (BST)

Figure 2: The Intermolecular Distances vs Time graph. The blue line is covered by the orange line as they have identical positions.

Figure 3: A closer look at the B-C line. The turning point of the graph occurs at distance around 0.91 Å. The flat region is where the transition state has been reached. The distance does not change dramatically after the turning point, as this indicates it approaches the saddle point (transition state) in the potential energy surface and tends to stay there.

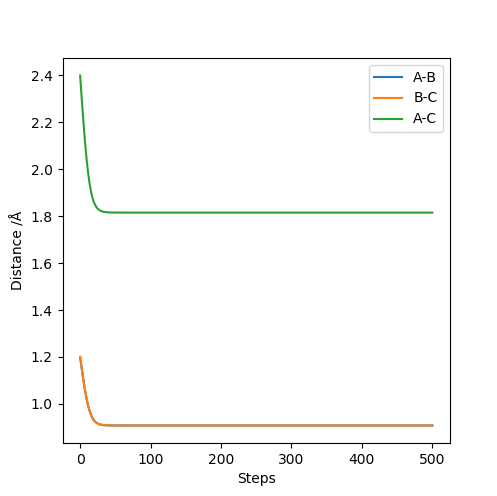
What do you mean by 'turning point', an inflection? I can't see a change in the curvature here.Fdp18 (talk) 09:17, 4 May 2019 (BST)

---

Minimum Energy Path (MEP) and Dynamic Trajectories

The differences between MEP and dynamic calculation types can be shown by the following:

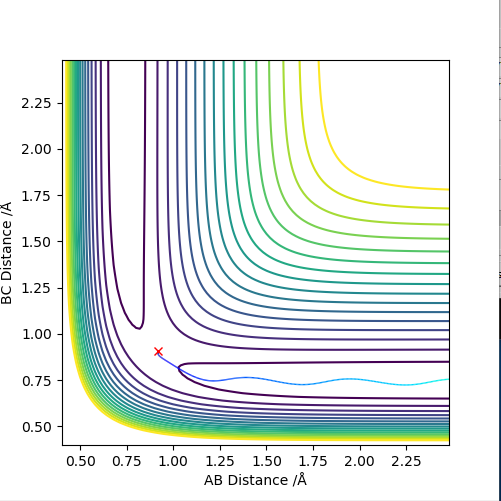
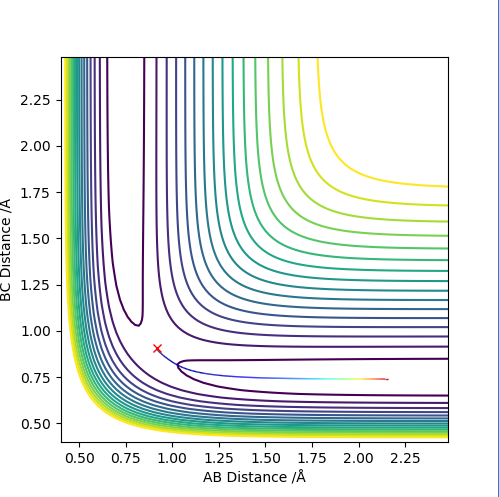
Figure 4: The contour plot of dynamics (above) and that of MEP (below). It can be seen that the dynamic calculation shows the fact that the molecule (the two atoms that are bonded to each other, in this case BC) is vibrating, on the contrast the MEP calculation does not show vibration (since MEP resets velocity to zero for each time step and hence KE = 0).

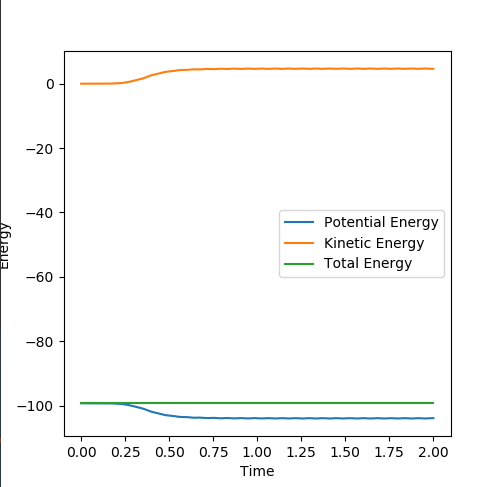
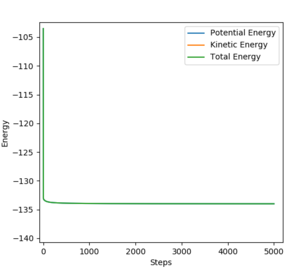
Figure 5: The Energy vs Time plot of dynamics (above) and that of MEP (below). The dynamic calculation shows a conservation of total energy by compensating the decreasing potential energy with rising kinetic energy, while the MEP calculation treats KE = 0 and hence the total energy equals to PE, both decreasing.

---

Reactive and unreactive trajectories

Trajectories with different combinations of momenta

p1	p2	Etot	Reactive?	Description of the dynamics	Figure no.
-1.25	-2.5	-99.018	yes	The molecule AB approaches C. B then leaves A and bonds to C via the transition state, forming molecule BC	6
-1.5	-2.0	-100.456	no	AB approaches C then it leaves C, as p2 is not big enough for reaction	7
-1.5	-2.5	-98.956	yes	AB approaches C. B then leaves A and bonds to C via transition state, forming BC	8
-2.5	-5.0	-84.956	no	AB (not vibrating) approaches C. B then leaves A and bonds to C (product formed), but B then goes back to A (re-cross transition state) and AB now vibrates	9
-2.5	-5.2	-83.416	yes	AB (not vibrating) approaches C. B then goes to C then back to A, but finally bonds to C, forming BC (vibrating)	10

It can be seen that larger momenta above the range (-1.5 < p₁ < -0.8 and p₂ = -2.5 for r₁ = 0.74, r₂ = 2.0) will not always result in a reaction.

That's not necessary the case, since you did not test all possible combinations (which are infinite). Think more about re-crossing and (leaving) the simple picture of TST.Fdp18 (talk) 09:22, 4 May 2019 (BST)

Figure 6

Figure 7

Figure 8

Figure 9

Figure 10

---

Main Assumptions of Transition State Theory

The follows are the five main assumptions of Transition State Theory:

1. Once the transition state towards the product has been crossed, the system cannot reform the reactants.

2. In the transition state, the reaction pathway motion can be viewed classically as translation and is separated from other motions.

3. The transition states to the products are distributed according to the Boltzmann distribution even if the system is not in equilibrium.

4. Born-Oppenheimer approximation applies: the electrons move on a time scale that the nucleus can be viewed as not moving.

5. Reactant molecules are distributed as described in Boltzmann distribution.

From the results obtained, it can be seen that under certain conditions the reactant will be reformed even if the transition state towards the product has already been passed by the system. This means that the experimental rates of reaction will be slower than the theory predicted values, due to the reformation of reactants in reality.

Indeed. Note also that 2. is not the case in the trajectories you calculated, there is usually some vibration even at or close to the TS. Keep in mind that other assumptions, like 4, could also be wrong, but can't be tested with the approach here since we are also using the Born-Oppenheimer approximation and can thus naturally not test for its violation.Fdp18 (talk) 09:26, 4 May 2019 (BST)

---

F-H-H system

be aware that 'F + H₂' doesn't define a reaction - you need the products to. How does the reader know that the reaction product is not 'FH₂' or three separated atoms?Fdp18 (talk) 10:17, 4 May 2019 (BST)

Figure 11. F + H₂, Exothermic, breaking H-H bond (+432 kJ/mol) and forming H-F bond (-565 kJ/mol).

Figure 12. H + HF, Endothermic, breaking H-F bond (+565 kJ/mol) and forming H-H bond (-432 kJ/mol)

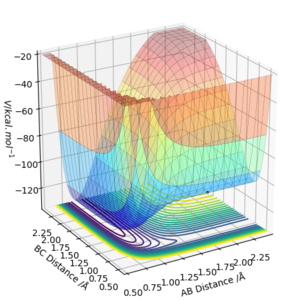
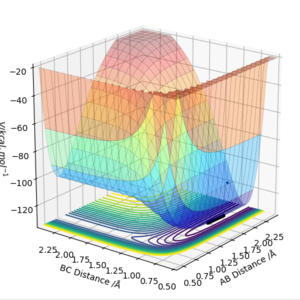
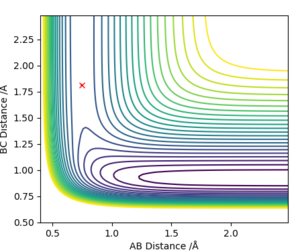
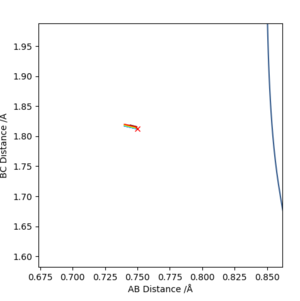
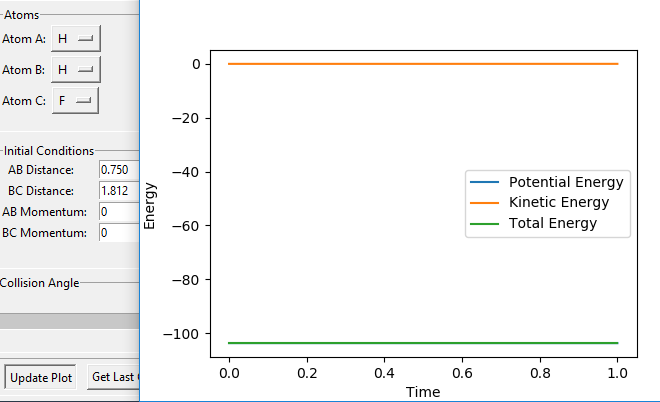
The transition state for F + H₂ is located at AB = 1.812 Å and BC (H₂) = 0.750 Å. It should be reversed for H + HF. Figure 13, 14 and 15 illustrate this by showing the locating position of transition state on the contour plot and the corresponding flattened energy plot:

Think about the statement 'It should be reversed'. The two plots you give below are redundant, as the PES inherently shows both H + HF, F + HH as well as the transition states and anything in between. Also be careful with your definitions and how you use them: the definition 'BC (H₂)' does not coincide with Figure 13. Although I could admittedly infer the definition from Figure 15, this shouldn't be necessary.Fdp18 (talk) 09:34, 4 May 2019 (BST)

Figure 13. The contour plot for locating the transition state(F + H₂).

Figure 13. The contour plot for locating the transition state(H + HF).

Figure 14. An enlarged version of the contour plot(F + H₂). The estimated position coordinate reported above is close to the actual position.

Figure 14. An enlarged version of the contour plot(H + HF). The estimated position coordinate reported above is close to the actual position.

Figure 15. The Energy vs Time plot(F + H₂). A flattened line indicates the transition state has been reached.

Figure 15. The Energy vs Time plot(H + HF). A flattened line indicates the transition state has been reached.

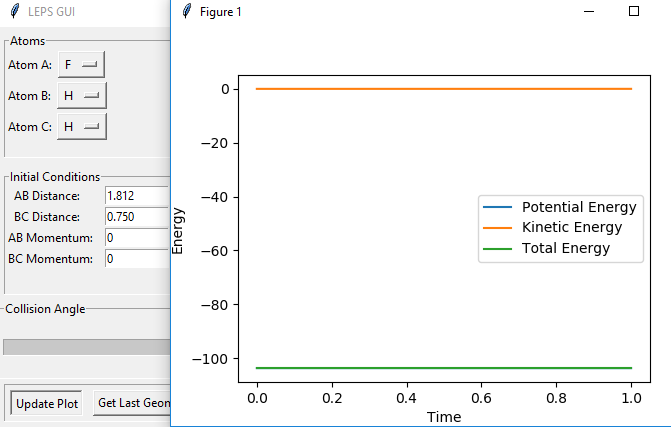
For F + H₂ the activation energy is found as +0.216 kcal/mol. This is shown by the difference in energies in Figure 16.

For H + HF the activation energy is found as +30.544 kcal/mol. This is shown by the difference in energies in Figure 17.

Figure 16

Figure 17

---

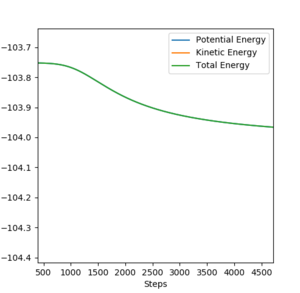
Mechanism of Release of Reaction Energy

The release of reaction energy is due to the increase in kinetic energy accompanied by the decrease in potential energy, as the total energy is conserved throughout. This idea can be illustrated by Figure 19. The effect of this can be observed, as the system will heat up (increase in KE results in increase in temperature).

As the energy is at first trapped in vibration, you can also get IR emission. Think back to all these gaussian calculations where you looked at vibrations, spectra and IR intensities. This is actually realised in my personal favourite, the fluorine laser, which works by combining fluorine radicals with H2.Fdp18 (talk) 09:39, 4 May 2019 (BST)

The initial conditions for obtaining Figure 18 and 19 (reaction occurs successfully) are set away from the transition state and lies on the reactant side, F + H₂: r₁ = 1.6 and r₂ = 0.725. p₁ = -0.4 and p₂ = -0.1.

Figure 18.The reaction pathway for F + H₂.

Figure 19.The Energy vs Time plot for F + H₂. The total energy is conserved throughout.

---

Distribution of energy and position of transition state

The location of energy barrier (early or late) is a very important factor in determining efficient distribution of energy of reactants which will make the reaction occur.

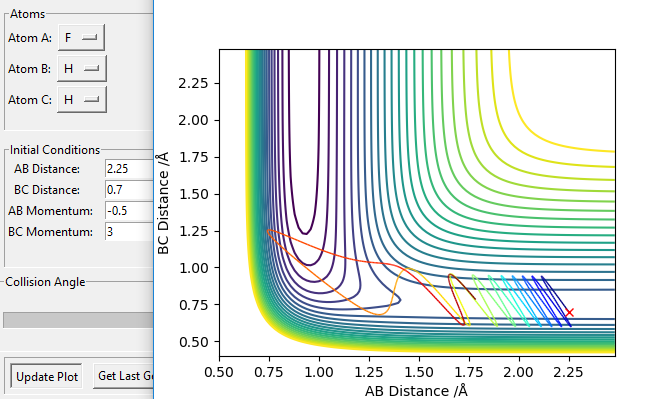
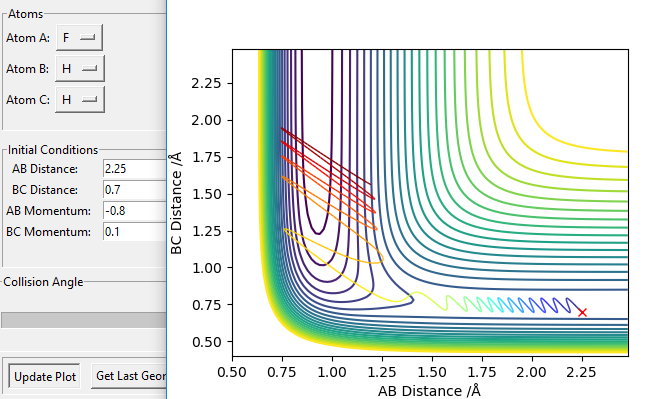
To cross an early energy barrier, translational energy is much more efficient than vibrational energy. This is modelled by the reaction F + H₂ (Figure 20 and 21). This reaction is exothermic, so according to Hommond's postulate the transition state resembles the reactant, i.e. an early energy barrier:

Figure 20.The reaction pathway for F + H₂. The parameters are set for low translational contribution and high vibrational contribution. The reaction does not occur. The molecule spends to much time on oscillating within the well and is not energetic enough to cross the barrier.

Figure 21.The reaction pathway for F + H₂. The parameters are set for higher translational contribution and low vibrational contribution. The reaction occurs successfully. The molecule now has enough energy directly on the reaction pathway and is able to cross the barrier easily.

On the contrary, the other reaction H + HF is endothermic so the transition state resembles the product, i.e. a late transition state. The vibrational contribution now matters significantly while the translational contributions does not. This can be illustrated by Figure 22 and 23:

Figure 22.The reaction pathway for H + HF. The parameters are set for very high translational contribution and a little vibrational contribution. The reaction does not occur. The molecule directly bounces back into the entrance.

Figure 23.The reaction pathway for H + HF. The parameters are set for small translational contribution and high vibrational contribution. The reaction occurs successfully. The molecule is vibrationally excited and is able to get to the top of the barrier with correct orientation.

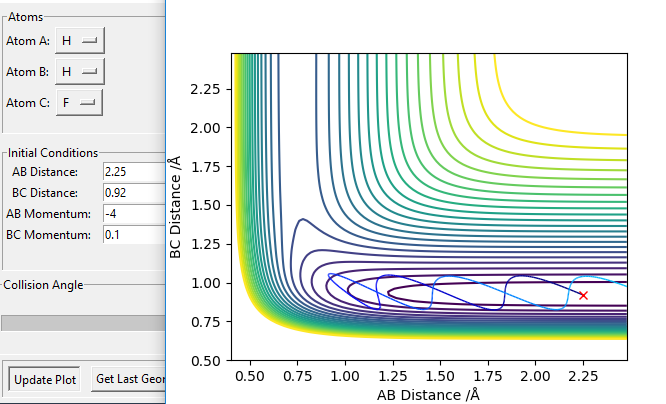
At the end, it may be worth noting that the above statement fits Polanyi's rule: vibrational energy leads to a late-energy barrier reaction more efficiently than translational energy. The examples above agree nicely with this by performing simulations and calculations, accompanied by analysis on the track of the reactant molecule.

The report is well structures and written, even with a nice 'abstract-like' sentence at the beginning. I also like the 'Transition States' part at the beginning, although I am not sure if you just copied that from somewhere. However, in dubio pro reo, so --> 5 MarksFdp18 (talk) 10:49, 4 May 2019 (BST)

---