MRD:01196775

Fig. 1: Internuclear separation vs time

EXERCISE 1: H + H₂ system

Dynamics from the transition state region

At a minimum, the first derivative of the graph ∂V(r1)/∂r1 is equal to zero, and the second derivative is larger than zero, implying an increasing curvature around the minimum. At a transition state, the first derivative is equal to zero and the second derivative is smaller than zero in one direction (a maximum), and larger than zero in the perpendicular direction (a minimum), implying that it is a saddle point. Good, so where is it in the energy surface diagram?--Sw2711 (talk) 14:59, 17 May 2018 (BST)

Trajectories from r₁ = r₂: locating the transition state

Fig. 2: Plots of the mep (left) and dynamics (right) calculations

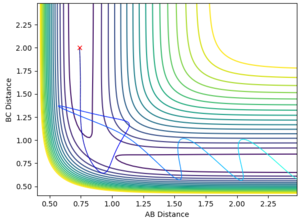
The best estimate of the transition state obtained in this investigation is r(ts) = 0.9077, as this results in minimal or no vibration of the atoms up and down the energy minimum curve on which the transition state rests. This can be seen from a plot of internuclear distances vs time (Fig. 1), in which it can be seen that the nuclei do not vibrate as they have no kinetic energy, i.e. they are not moving along any energy gradients and the system is balanced at the transition state.

Good--Sw2711 (talk) 15:00, 17 May 2018 (BST)

Trajectories from r₁ = r_ts+δ, r₂ = r_ts

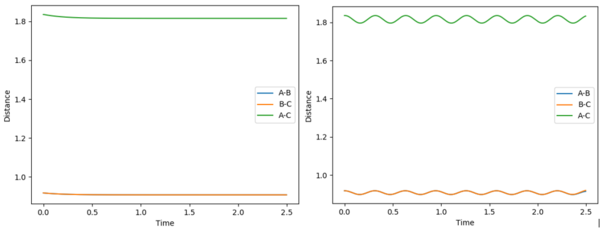
The minimum energy path (mep) for an internuclear separation of r= r(ts) + 0.01 shows a smooth decrease in distance towards the transition state internuclear separation, as it does not account for momentum of atoms due to mass and velocity. Due to mass and velocity? I think you just need to say the velocity resets to zero at each time step--Sw2711 (talk) 15:04, 17 May 2018 (BST)The 'Dynamics' calculation does take these factors into account and therefore shows that when the atoms start off at a distance different to the transition state distance, they oscillate as they have been given momentum, or in other words the bond has vibrational energy.

Reactive and unreactive trajectories 

For r1 = 0.74 and r2 = 2.0, an investigation was conducted into whether a series of combinations of momenta were reactive and what their total energy was.

p1	p2	Total energy	Trajectory is reactive: Y/N	Plot	Description
-1.25	-2.5	-99.119	Y		Reaction proceeds with normal oscillation from reactants to products
-1.5	-2.0	-99.119	N		Reactants approach transition state and do not have enough momentum (kinetic energy) to cross the barrier, so revert to reactants
-1.5	-2.5	-99.119	Y		Reaction proceeds with normal oscillation from reactants to products
-2.5	-5.0	-99.119	Overall unreactive		Reaction crosses over transition state and then returns to reactants, with vigorous bond vibration at completion
-2.5	-5.2	-99.119	Y		Reaction proceeds vigorously with movement over higher energy forms of the transition state and initially reversion, on the way to the products

Assumptions in transition state theory

1. The Born-Oppenheimer approximation is used, meaning that quantum tunnelling by electrons is not considered. This means that motion along the reaction coordinate can be considered as a classical translation.
2. The energies of the transition states which are reacting to form products follow the Boltzmann distribution, even when the reaction has not yet reached dynamic equilibrium.
3. Once the transition state has been reached and there is momentum in the direction of the products, there will be no reversion to reactants.

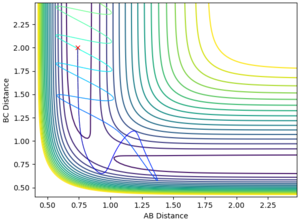
These assumptions are however observed to be incorrect according to these simulations, as the fourth simulation shows the reactants crossing the transition state and then returning. Transition state theory would agree well with the experimental rate values for reactions which follow its assumptions, such as the first, second and third reactions, but would give poor approximations to the final two. In the fourth simulation, the third assumption of transition state theory is broken; the reaction crosses the transition state and then reverts to the reactants. This shows that it is a simplification to claim that it is only momentum in the direction of the products is required, and there are cases where too much energy is supplied and the product bond vibrates so violently that it shakes itself apart to products again. The fifth case demonstrates that this barrier recrossing can happen multiple times, if more vibrational energy is supplied. Transition state theory would predict a higher rate than experimental values in the fourth and fifth cases as it does not account for the time spent on reversion.

The five tests above and this part are both good. Just one point, you probably notices that the boltzmann distribution is not very applicable in our case, as we only have three atoms in our system. --Sw2711 (talk) 15:08, 17 May 2018 (BST)

EXERCISE 2: F - H - H system

Fig. 3: Surface plot for the F + H₂ reaction, with the reactants (F + H₂) on the higher energy, right hand side and the products (H + HF) on the lower energy, left hand side.

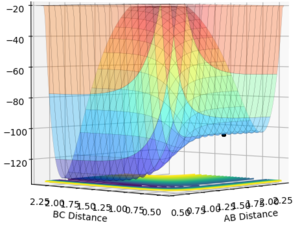
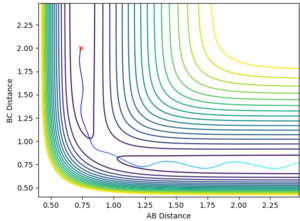
Sorry, I have to break your paragraph into parts, as there are a few marking points here--Sw2711 (talk) 15:16, 17 May 2018 (BST) The  F + H₂ reaction is exothermic and the H + HF reaction is endothermic as the F + H₂ system lies on the higher energy side of the surface plot (Fig. 3) and H + HF on the lower energy side. This implies that the H-F bond is stronger than the H-H bond. Good, you have explanation and evidence. --Sw2711 (talk) 15:16, 17 May 2018 (BST)

The transition state is located at AB distance 1.808 and BC distance 0.751. This was identified as it was within the BC = 0.751 energy trough, and far enough along the AB separation that the system remained balanced at the transition state and did not slide to the products. Good, but I will need some evidence. --Sw2711 (talk) 15:16, 17 May 2018 (BST)

The potential energy of the transition state is -103.738 kcal/mol, that of F + H₂ is -103.793 kcal/mol and that of H + HF is -133.772 kcal/mol. Therefore the activation energy for the formation of H + HF is +0.055 kcal/mol and the activation energy for the formation of F + H₂ is +30.034 kJ/mol. Again, I need some evidence--Sw2711 (talk) 15:16, 17 May 2018 (BST)

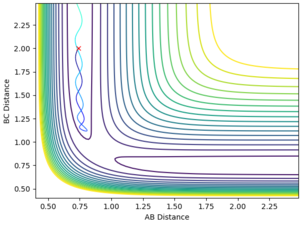
The reaction energy is released by the greater amplitude of vibration of the H-F product bond compared to the H-H reactant bond, therefore dissipating the energy to the surroundings through kinetic motion (Fig. 4), though the simulation doesn't show this eventual removal of energy from the system. This could be confirmed experimentally by measuring an increase in temperature during the reaction as energy is transferred to the surroundings by this increased amplitude of bond vibration. Good--Sw2711 (talk) 15:16, 17 May 2018 (BST)

Fig. 4: Internuclear momenta for the reaction of F +  H₂, showing that the H + HF products have greater internuclear momenta than the reactants.

Polanyi's empirical rules

Fig. 5: Reactive trajectory from H + HF to F + H2

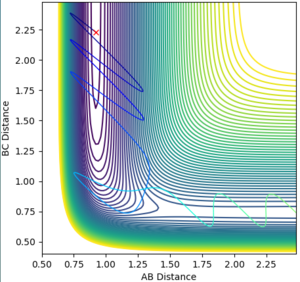
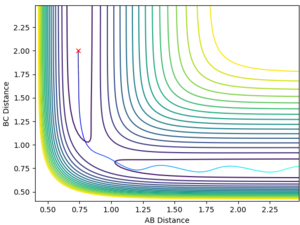
A reactive trajectory is obtained with an AB distance of 0.92, BC distance of 2.23, AB momentum of -10 and BC momentum of -1 (Fig. 5). This relates to Polanyi's empirical rules, which state that kinetic/translational energy is ineffective in causing a system to cross a late transition state (i.e. that of the endothermic reaction of HF + H) and that only vibrational energy is effective in crossing such a barrier. Good. Just to be precise, translational and vibrational are two types of kinetic energy. It is a bit weird when you say 'kinetic/translational' energy--Sw2711 (talk) 15:16, 17 May 2018 (BST)

This leads to the release of energy by product translation rather than by product bond vibration, after the reaction has proceeded. The vibrational energy supplied is represented in the simulation as momentum between F and H, and it is observable in Fig. 5 that the product H-H bond has less momentum, or lower amplitude vibration than the reactant H-F bond at the start of the reaction, and that the H₂ product translates away from F. The inverse of all the above statements is true for an early transition state, as in the case of the reaction of F + H₂, and it is thus observed that only translational energy is able to cause crossing of the transition state and that the products release their energy by bond vibration, shown in Fig. 4 as greater internuclear momentum in the product H-F bond. Good--Sw2711 (talk) 15:16, 17 May 2018 (BST)

References