MRD:01188093

H + H2

Minima and Transition States

At both the minimum and the transition state the ∂V(ri)/∂ri =0. Another way to express this is that the gradient is zero.

The key difference between a minimum and a transition state is that the minima are at a global minimum whereas the transition state is at a saddle point. The transition state is at a saddle point as if we move along the reaction pathway the energy reaches a minimum but if we deviate from the reaction pathway the energy increases.

At a minimum changing the coordinates slightly will result in the perturbed structure reverting to the structure at the minimum point whereas perturbing the structure at the transition state will result in the structure moving to the structure at the minimum state.

Jas213 (talk) 14:33, 15 May 2018 (BST) You mentioned the gradient, but didn't discuss the curvature (second derivative) at all. You need to talk about the second derivative to determine whether you have found a minimum or a transition state. It would have been expected from you to discuss the increased complexity dealing with a 3D surface, instead of the conventional 2D picture. Next time, there is no harm in citing a reference that you needed to consult in order to answer this question in more detail.

Determining the Transition State

Best guess of r_ts = 0.90812

Jas213 (talk) 14:37, 15 May 2018 (BST) What are you implying by just giving me one distance? What does r_ts refer to? How does it relate to the AB, BC distance. Stating just best guess and the number is not enough. What was your method used when trying to find the transition state? What's the unit of r?

The theory states that at an a certain Internuclear Distance, the trajectory will oscillate and never fall off the saddle point. This is represented by a completely flat line on the graph of Internuclear Distance against time.

As we can see above using the provided r_ts results in a very flat line and thus this is the internucular distance that results in this.

Jas213 (talk) 14:37, 15 May 2018 (BST) Correct, do more explanations such as this one!

Minimum Energy Pathway (MEP) versus Dynamic Trajectory

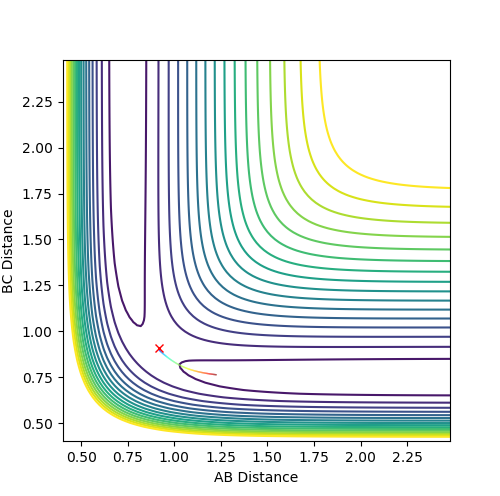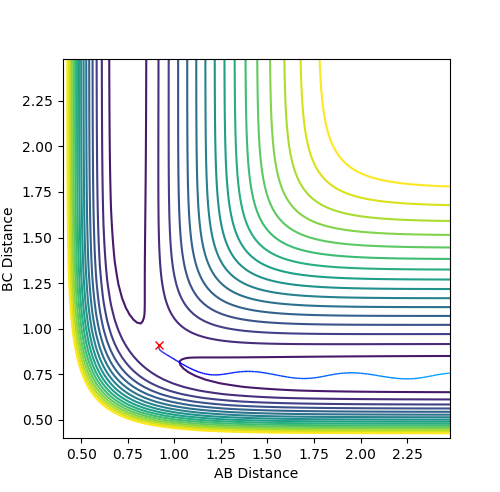
The MEP of the System	The Dynamic Trajectory of the System

Also known as the reaction coordinates, the MEP is the reaction pathway if at each stage the velocity was reset to zero and hence there was no vibrations.

In comparison, the dynamic trajectory is a more realistic picture that takes into account that the molecules will have momentum and more importantly inertia and they will thus oscillate, taking a less direct path.

Jas213 (talk) 14:39, 15 May 2018 (BST) You could have illustrated this even more with Internuclear Distance vs. Time plots or Momentum vs. time plots. Connect your statement to the fact that one line is wiggly, the other is not, one trajectory is shorter than the other. Generally try to give more detailed descriptions.

Reactive and Unreactive Pathways

For a system to be reactive the molecules must collide with enough kinetic energy to overcome the activation energy (the energy required to reach the transition state). The kinetic energy will be converted to potential energy in order to form the higher energy transition state.

We would thus assume that, at a set distance, increasing the momentum and thus the kinetic energy that the reaction would always go to completion past a certain threshold. Jas213 (talk) 14:52, 15 May 2018 (BST) Good that you mention the connection between momentum and kinetic energy, it would have been even more useful if you had also given the proportiong of kinetic and potential energy for each trajectory.

p1	p2	Energy (kcal/mol)	Reactive / Unreactive
-1.25	-2.5	-99.018	Reactive
-1.5	-2.0	-100.463	Unreactive
-1.5	-2.5	-98.956	Reactive
-2.5	-5.0	-84.956	Unreactive
-2.5	-5.2	-83.416	Reactive

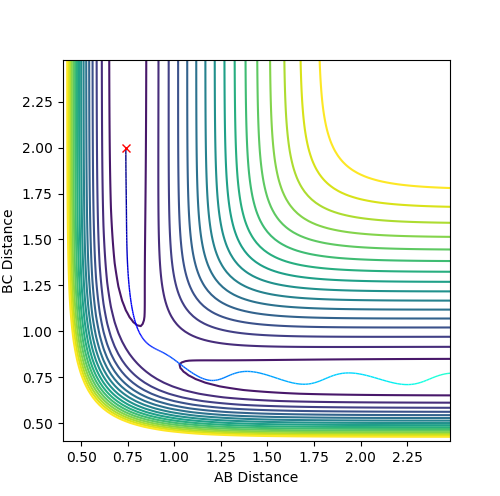	Here the trajectory is reactive as the pathway shows the molecules moving from one side of the graph to the other through the transition state. Approaching the transition state the B-C distance decreases and after the A-B distance increases. After the saddle point the new H-H bond is osicallating more.
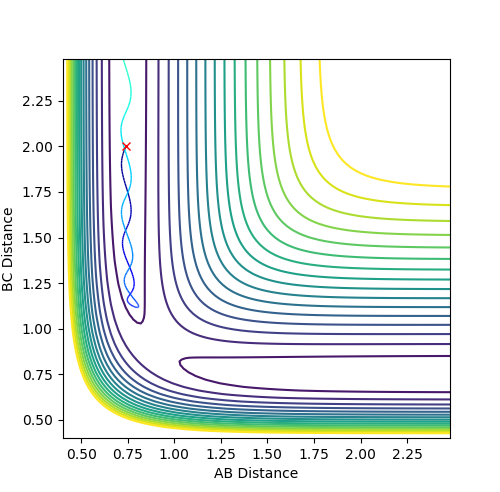	Here the trajectory is unreactive as the reaction pathway doesn't move from the reactant side to the product side of the graph. The molecules do not have enough kinetic energy to reach the transition state and thus the reaction doesn't proceed.
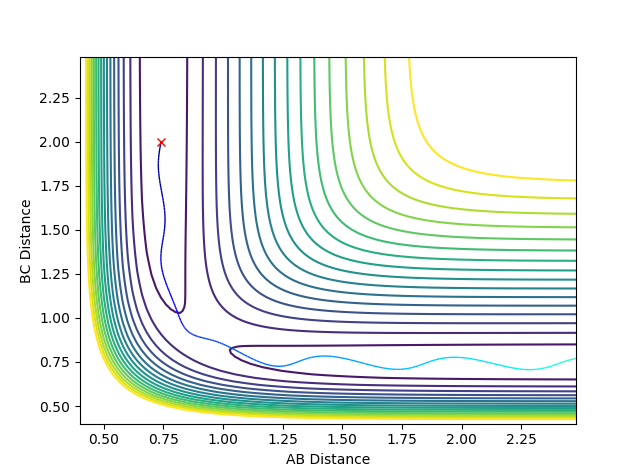	Here the trajectory is reactive as the pathway shows the molecules moving from one side of the graph to the other through the transition state. In comparison to conditions 2 we have increased the value of p2, increasing the momentum of the system will increase the kinetic energy thus allowing the system to reach the transition state and thus react.
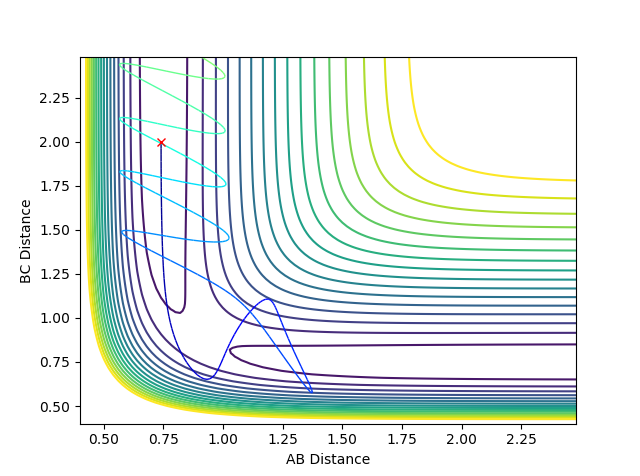	We would assume based on the previous logic that increasing the kinetic energy of the system more as is the case here would allow the reaction to go to completion as there is more kinetic energy available which can be converted to potential energy allowing the system to reach the transition state. Here is a clear demonstration of the failure of this logic. In this scenario the reaction pathway does not result in a the path moving from the reactants to the products side. This is an example of barrier recrossing. B does temporarily swap sides and reacts with A but the vibrational energy causes the molecules to move into the range of each other and thus B swaps back to C. Jas213 (talk) 14:52, 15 May 2018 (BST) Good that you are trying to explain what's going on, and you mentioned vibrational energy, and generally talked about kinetic energy. instead it would have been clearer if you had discussed the varying proportions of vibrational and translational energy.
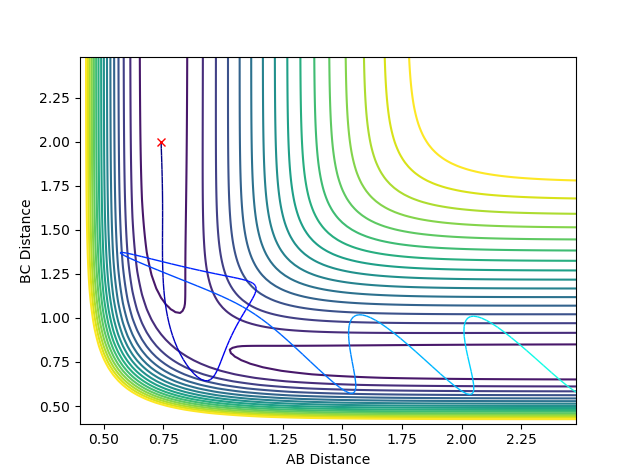	Here the trajectory is reactive, as we can see that the pathway ultimately ends up in the products side of the graph. Here, the H atom approaches the non-vibrating H2 molecule. There is enough energy to cause a vibrationally excited A-B-C complex and the B atom changes the position of the bond several times between A and C before ultimately remaining close to A and ending up in a vibrationally excited A-B molecule as indicate by the oscialltion of the pathway after the transition state.

Jas213 (talk) 15:23, 15 May 2018 (BST) A concluding remark about what you learned from this table would have been expected.

Main Assumptions of Transition State Theory

There are three main assumptions:

1. The atoms behave according to classical mechanics

2. There is a quasi-equilibrium between the transition-state and the reactants.

3. The reaction will pass through the lowest energy transition state only.

The consequences of these assumptions are severe, the first one precludes any quantum mechanical phenomena such as tunneling. This means that even in a system where the molecules don't have enough energy to reach the transition state some of the molecules will still react and form the product.

The quasi-equilibrium doesn't involve the products. i.e. one the system has reached the products the pathway can't reverse causing the products to revert to the reaction. This means that transition state theory doesn't take into account barrier recrossing which can be significant.

The net result of this is that transition state theory will predict a higher rate than what is observed experimentally due to barrier recrossing not being considered in the theory.

Jas213 (talk) 14:56, 15 May 2018 (BST) Very clear and nice citation style. Correct.

F - H - H System

Energetics

Classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?

The left of the graph is the F and H-H system which is higher in energy. The right of the graph is the H-F and H system which is lower in energy

F + H2 is exothermic. H + HF is endothermic

This is justified as in the first reaction you are breaking a H-H bond and the formation of H-F. The H-H bond is weaker than the H-F bond so the energy that is put in to break the H-H bond is reimbursed by the energy released by the formation of the H-F bond. This results in a net decrease in energy of the system which is classified as an exothermic reaction.

In contrast, the second reaction involves the breaking of a strong H-F bond and the formation of the weaker H-H bond so overall, energy must be put in to cause the reaction to proceed hence the reaction is endothermic.

Jas213 (talk) 15:00, 15 May 2018 (BST) Overall correct, but too short and lacking details. It is correct that the HF bond is stronger and HH is weaker compared with one another, but it's not the level of detail one would expect in a handed-in report. Why is one bond weaker/stronger than the other? You could have stated some bond energies to prove this.

Locate the approximate position of the transition state.

We know that in an exothermic reaction, by using Hammond's postulate, we can approximate the transition state as resembling the starting material. In this case, it was assumed that the bond length would be similar to the bond length of the H2 atom. Jas213 (talk) 15:25, 15 May 2018 (BST) Good that you stated the assumption that helped you to find the TS, but what was your actual method? H-H Distance: 0.746 Angstrom

F-H Distance: 1.810 Angstrom

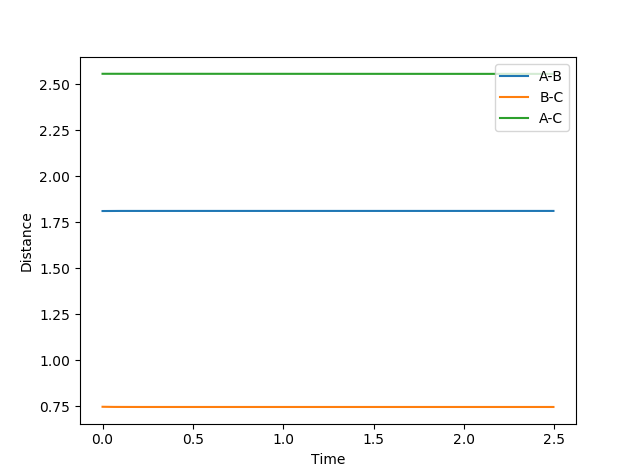Jas213 (talk) 15:25, 15 May 2018 (BST) Was this distance plot obtained from dynamics or MEP? Which method did you use to confirm your TS?

Report the activation energy for both reactions.

The activation energy is the difference in energy between the reactants and the transition state. In terms of the graph this can be thought of as the energy gap between the minima and the saddle point.

To find the activation energy the method used was to vary the internucular distances by a small amount and the record the MEP. By looking at the energy vs. time graph we see that the gap between the two horizontal lines is the activation energy.

F H - H System

Energy of the TS:-103.743 kcal/mol

Energy of the Reactants: -103.882 kcal/mol

Activation Energy: -0.139 kcal/mol

The TS state is higher in energy than the reactants, hence you would expect a positive activation energy.

H H - F System

Energy of the TS: -103.743 kcal/mol

Energy of the Reactants: -133.908 kcal/mol

Activation Energy: 30.165 kcal/mol

In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. How could this be confirmed experimentally?

We know, by using the second law of thermodynamics, that energy can neither be created or destroyed, rather it must be converted from one form to another.

In the reaction there are two types of energy: potential energy which is stored in the bonds, and kinetic energy which is expressed as translational energy and vibrational energy.

As the reaction between F and H-H is exothermic we know that the potential energy decreases as the products are more stable than the reactants. As such, we would expect, through the use of the Laws of Thermodynamics, that the kinetic energy would increase by the same amount to compensate. This would present itself as an increase in the vibrational energy which would be seen as an increase in the amplitude of the vibration. We can observe this by monitoring the internuclear momentum. We would expect for a successful reaction that the internuclear momentum will increase in response to the amplification.

We can see in the above graph that the amplitude of the oscillation is greater after the collision ie. the oscillation of A-B is larger than B-C, thus confirming that the released energy is converted into vibrational energy.

We can test this hypothesis in the lab by doing calorimetry. Temperature is proportional to the average kinetic energy of the molecules thus, we would expect that the temperature recorded would increase as the reaction occurred.

Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.

Polanyi's Rules are a set of empirical observations that show that different forms of energy are more effective at promoting the formation of the transition state than others . Polanyi showed that in a system with an early transition state that translational energy is more efficient tha vibrational energy in forming the transition state. In a system with a late transition state the opposite is true. i.e. vibrational energy is more efficient than translational energy in forming the transition state.

We know the reaction between F and H2 is exothermic. This means that, according to Hammonds postulate, the transition state will closely resemble the reactants and hence there will be an early transition state. By applying Polyani's Rules we would thus expect that a system with a high translational energy would result in a reactive system.

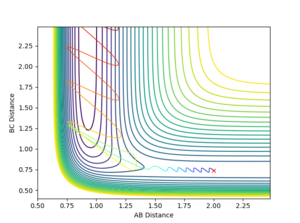
To explore this two scenarios were conducted. In the program p1 corresponds to translational energy and p2 corresponds to vibrational energy.

In the first scenario there is high translational energy and low vibrational energy which, as we can see, resulted in a reaction. In the second scenario there is highvibrational energy and low translational energy, as we can see resulted in an unreactive trajectory. If kinetic energy in both its forms was equally as effective as promoting the transition state in both cases the molecules should react. That is not the case.

In this case, p1 = -0.8 and p2 = 0.1

In this case, p1 = -0.1 and p2 = 0.8

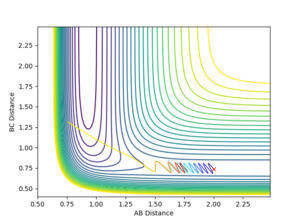Hence, this shows that for this system the Polanyi Rules apply.

In contrast, we know that the reaction between H and HF is endothermic hence, by applying Hammond's Postulate, we know that the transition state will be late. As such, by applying Polanyi's rules we would expect that vibrational energy would be more effective in promoting the transition state than translational energy.

In this case, p1 = -5 and p2 = 5

In this case, p1 = -3 and p2 = 8.5

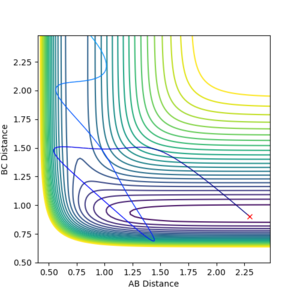As we can see here, the higher vibrational and low translational energy system is the one which reacts in contrast to the system above where the opposite happens. Again, this is a demonstration of Polanyi's Rules Jas213 (talk) 15:22, 15 May 2018 (BST) Good that you mentioned Polanyi's rules and tried to relate it to your PES trajectories.