MRD:01188090
Exercise 1: H + H2 system
Dynamics from the transition state region
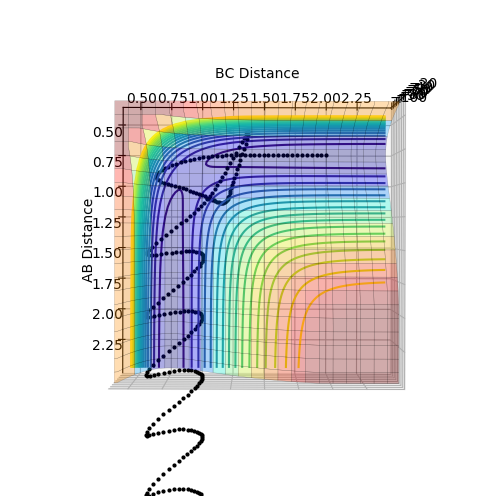
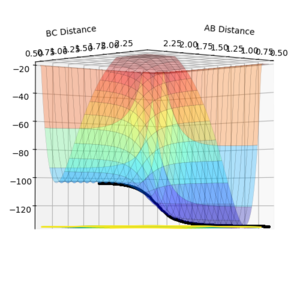
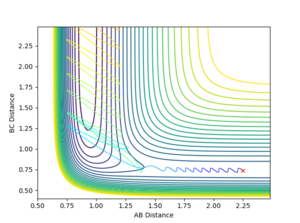
The transition state can be shown on a potential energy surface at the saddle point, which is where the function is a maximum with respect to one variable, but a minimum in respect to the other variable, shown in figure 1. The gradient for the transition point and the minimums are both found to be zero, ∂V/∂rAB=∂V/∂rBC=∂V/∂rAB∂rBC=0, but can be distinguished by taking the second derivative of the gradient.
Trajectories from r1 = r2: locating the transition state
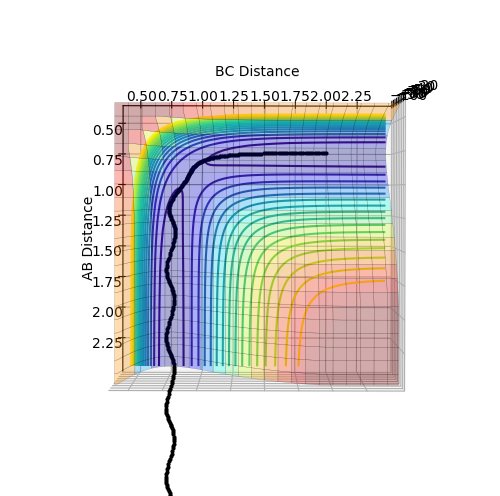
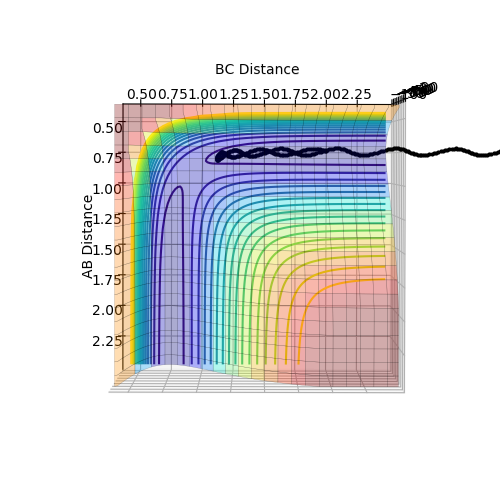
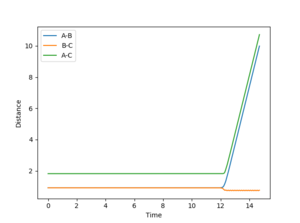
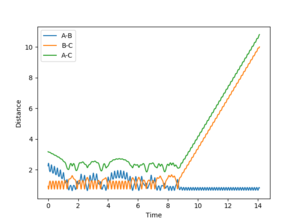
In order to prevent the molecule from moving out of the energy minima, the momenta for both AB and BC are set to zero. By comparing the contour plot and the internuclear distance vs time plot (Figure 2), it can be seen that the the approximate bond length for the transition state is 0.908 Å. When both distance AB and BC are set to this distance, the internuclear distance vs time plot (Figure 3) initially shows the molecule is in the transition state, as there is no vibrations present, however after 12 seconds, the molecule leaves the transition state and vibrations can be seen.
Trajectories from r1 = rts+δ, r2 = rts
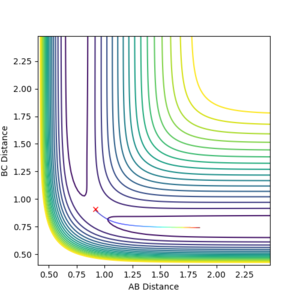
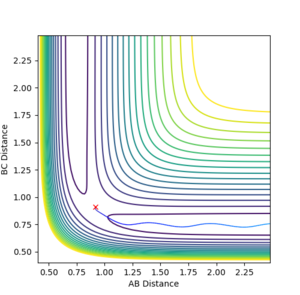
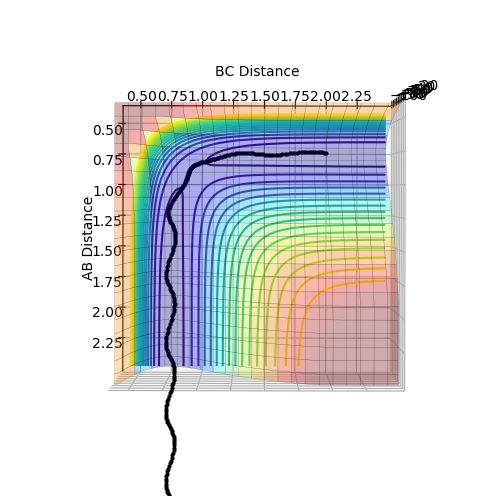
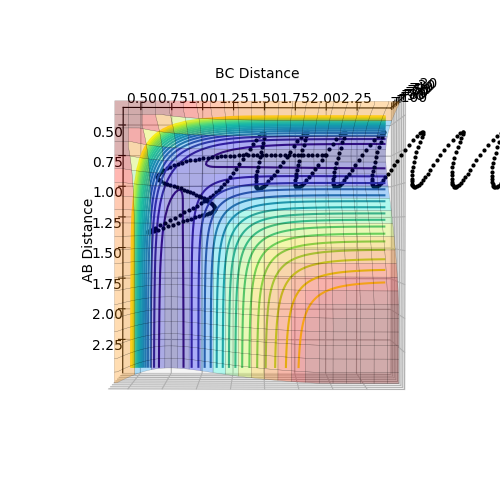
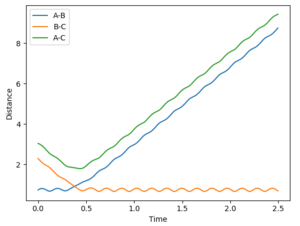
The minimum energy path (mep) shows the reaction path that has the lowest energy. As shown in Figure 4 and 5, the reaction path goes from the transition state towards the products in both cases, however for the mep it can be seen that the molecule is not vibrating and the reaction does not go to completion (Figure 4), whereas when the trajectory is set to dynamic, the molecule is vibrating and the product is formed (Figure 5).
Ng611 (talk) 13:43, 1 June 2018 (BST) Good. Why is this the case though? What differences in the algorithms lead to this difference.
Reactive and unreactive trajectories
The following reactions were carried out using distances AB = 2.0 and BC = 0.74 to test the effect of different momenta between atoms on the reactivity of the system.
| Reaction | p1 | p2 | Total Energy | Trajectory Plot | Reactive or unreactive? | Discussion | |
|---|---|---|---|---|---|---|---|
| 1 | -1.25 | -2.5 | -99.018 |  |
Reactive | As C approaches AB, the straight line trajectory shows that AB aren't vibrating. The trajectory then passes through the transition state and into the product pathway, however the trajectory shows slight vibration between the newly formed BC, shown by the wavy line. | |
| 2 | -1.5 | -2.0 | -100.456 |  |
Reactive | As C appraoches AB, AB are vibrating, shown by the wavy black line, however, the trajectory does not cross the transition state and AB and C move away from each other, with AB vibrating in the same manner as when C was approaching. | |
| 3 | -1.5 | -2.5 | -98.956 |  |
Unreactive | As C approaches AB, AB is vibrating, as shown by the wavy black line. The trajectory then passes through the transition state, and passes down towards the products, showing BC vibrating. | |
| 4 | -2.5 | -5.0 | -84.956 |  |
Unreactive | The system crosses the transition state barrier, forming a BC bond and breaking the non-vibrating AB bond, however after time, the system crosses back over the transition state barrier and the trajectory follows the path back towards the reactants, with AB vibrating strongly. | |
| 5 | -2.5 | -5.2 | -83.416 |  |
Reactive | The reaction path crosses the transition state barrier into the pathway of the products, before briefly returning to the reactant pathway. However, after time the system crosses the transition state barrier, forming BC, which vibrates strongly as A migrates away. The reaction pathway shows that AB is not vibrating. |
Transition state theory is based around a few main assumptions: Firstly, the reactants and the products are seen as two separate states, separated by a transition state barrier. Once the reaction path crosses this barrier, it is assumed that the reaction path cannot recross the barrier back towards the reactants. Furthermore it is assumed that the reactants behave classically and cannot quantum tunnel.3 Reaction 4 shown above discredits transition state theory as although the activation barrier is crossed and the reaction path initially moves towards the products, after time it is seen that the product is able to recross the barrier, thus dissociating back to the reactants. Furthermore, this disagrees with the assumption that the system behaves classically, as it would be seen that once the reactant molecules react with enough energy to form the transition state, the reaction would then proceed to form the products irreversibly, however this is also not observed in the case of reaction 4. As the theory assumes that once the transition state is formed, the reaction will proceed straight on to the products and doesn't take other processes into account, e.g. barrier recrossing, it would be expected that the theory will predict a faster rate of reaction to those observed experimentally.
Ng611 (talk) 13:47, 1 June 2018 (BST) Good. How will tunelling affect the reaction rate relative to the one predicted by TST?
F-H-H Sytems
The forward reaction in the equilibrium F + H2 ⇌ H + HF is exothermic1 as the HF bond (565 kJmol-1) is stronger than the HH bond (432 kJmol-1)2, therefore the energy required to break the HH bond is more than the energy required to form the HF bond, thus there is an overall release of energy. The HF bond is stronger as there is a greater electronegativity between the two atoms. As a result the backward reaction is endothermic.
PES Inspections
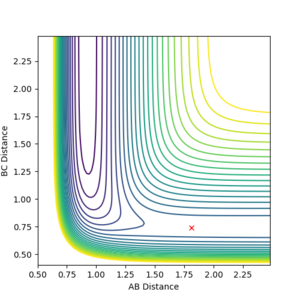
Assuming atom A is a F atom and atoms B and C are H atoms, the following approximate momenta and distances show a transition state for the F + H2 ⇌ H + HF reaction: AB distance = 1.81 Å, BC distance = 0.74 Å, AB momentum = 0, BC momentum = 0. These approximate parameters are found by applying Hammond's Postulate, which implies that the transition state in a reaction will resemble the reactants or products more, depending on which one they are closer in energy to. Both the forward and backward reactions show the same transition state.
Activation Energy
In the forward reaction, the energy of the transition state is -103.75 kJmol-1 and the energy of the product is -104.02 kJmol-1.Therefore, the activation energy for the forward reaction is 0.27 kJmol-1. (Figure 8)
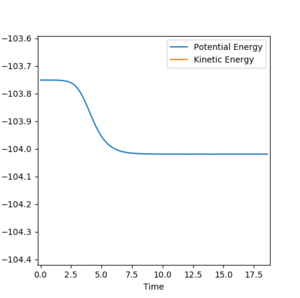
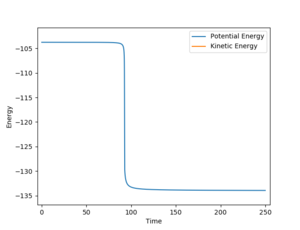
In the backward reaction, the energy of the transition state is -103.75 kJmol-1 and the energy of the products is -133.93 kJmol-1.Therefore, activation energy for the backward reaction is 30.18 kJmol-1. (Figure 9)
Reaction Dynamics
AB distance = 2.25
BC distance = 0.74
AB momentum = -1
BC momentum = 0
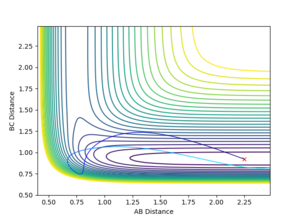
The graphs above (Figures 10 and 11) show that the energy released during the exothermic reaction are converted into vibrational energy as the reactants are only vibrating a small amount in comparison with when the reaction path passes through the transition state and into the products, where the products have a large amplitude of vibration.
Ng611 (talk) 13:48, 1 June 2018 (BST) How can this be confirmed experimentally?
A and B are H atoms, C is an F atom.
AB distance = 2.25
BC distance = 0.92
AB momentum = -0.5
BC momentum = -9
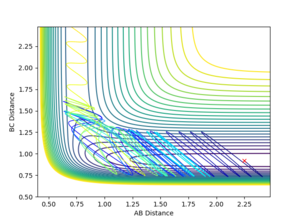
The above graphs (Figures 12 and 13) show the reaction path crossing and recrossing the transition state barrier multiple times, before proceeding to the products with a smaller vibrational amplitude.
The above graph (Figure 14) shows a counterexample of how a large translational energy and a relatively large vibrational energy will not allow the reaction path to proceed towards the products.
A and B are H atoms, C is an F atom.
AB distance = 2.25
BC distance = 0.92
AB momentum = -9
BC momentum = -0.5
Polanyi's rules state that a reaction with an early transition state will be dominated more by translational moments than by vibrational moments, whereas a late transition state will be dominated predominantly by a larger vibrational moment than a larger translational moment.4
As shown above, the forward reaction, which is exothermic, has an early transition state and in order for the reaction pathway to cross the transition state barrier to the products, a high translational energy is of the reactants is required as shown.
Furthermore, the backward reaction is exothermic, and a larger vibrational energy and smaller translational energy is required in order to allow the reaction to proceed and for the products to form. The counterexample further proves that a large translational energy will not allow the reaction path to proceed past the transition state barrier, thus obeying Polanyi's rules.
Ng611 (talk) 13:49, 1 June 2018 (BST) If the forward reaction is exothermic, then the backward one must be endothermic. Otherwise, a very good second section and a very good overall report. Well done!
References
[1] - J.C. Polanyi, D.C. Tardy, 1969, J. Chem. Phys., Vol.51 "Energy Distribution in the Exothermic Reaction F + H2 , and the Endothermic Reaction HF + H", p.255-321
[3] - J. E. Meany, V. Minderhout and Y. Pocker, J. Chem. Educ, 2001, 78, 204.
[4] - Z. Zhang et al, J.Phys. Chem. Lett., 2012, "Theoretical Study of the Validity of the Polanyi Rules for the Late-Barrier Cl + CHD3 Reaction", Vol. 3 (23) p.3416–3419