MRD:01180512

Exercise 1: H + H₂ System

Ng611 (talk) 12:03, 22 May 2019 (BST) An exemplary report that clearly demonstrates mastery of the subject matter. Your use of the Hessian to see the TS was particularly good (and is actually how computation chemistry packages determine the TS). Overall, this is an outstanding piece of work

Transition State

The transition state is a turning point and has a partial derivative of 0 with respect to all its axes. The transition state is a saddle point and can be found using the Hessian matrix, whose elements would be the partial derivatives of energy against distance in along a particular axis for a reaction coordinate as shown below. The determinant of the Hessian Matrix would be positive when there are local minima or maxima. If the determinant is negative, then it is a saddle point. ^[1]

$H = [\begin{array}{ll} f_{x x} & f_{x y} \\ f_{y x} & f_{y y} \end{array}]$
where $D_{1} = f_{x x} and D_{2} = \det H = | \begin{array}{ll} f_{x x} & f_{x y} \\ f_{y x} & f_{y y} \end{array} |$
If $D_{1} (a, b) > 0$ and $D_{2} (a, b) > 0$ , then $f$ has a local minimum at $(a, b)$
If $D_{1} (a, b) < 0$ and $D_{2} (a, b) > 0$ , then $f$ has a local maxima at $(a, b)$
If $D_{2} (a, b) < 0$ , then $f$ has a saddle point at $(a, b)$

In addition, the eigenvalues of the Hessian at a reaction coordinate will also reveal the presence of a saddle point. If the eigenvalues of the Hessian have both a positive and a negative value, both concave up and concave down properties are present simultaneously, implying a saddle point is present since a positive eigenvalue implies minima and a negative eigenvalue implies a maxima. ^[2]

Ng611 (talk) 11:48, 22 May 2019 (BST) This is an exemplary answer! Really well done!

Estimation of the Transition state

F = - \frac{\partial V (a, b)}{\partial R}

The Force acting on the Hydrogen atoms can be represented by the negative of the gradient of the potential energy with respect to distance. As established earlier, the gradient at the transition state is zero, and this can be estimated by looking at the 'forces' section of the graphical user interface (GUI).

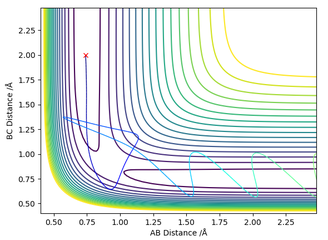
The estimation for the transition state bond length was achieved by using a simple harmonic oscillator (SHO) approximation of the oscillation of the H atoms when R_{H_AH_B} = 0.83 Å and R_{H_BH_C} = 0.83 Å, and P_{H_AH_B} = 0 and P_{H_BH_C} = 0. Using an interdistance vs time plot, the position of 'zero' displacement in a SHO gave the position of the Transition state, since the Force is 0 when the displacement is zero (SHO approximation). This position of 'zero' displacement is found to be 0.907742 Å, which was verified by looking at the 'forces' section of the GUI. The forces were 0, which indicated a stationary point.

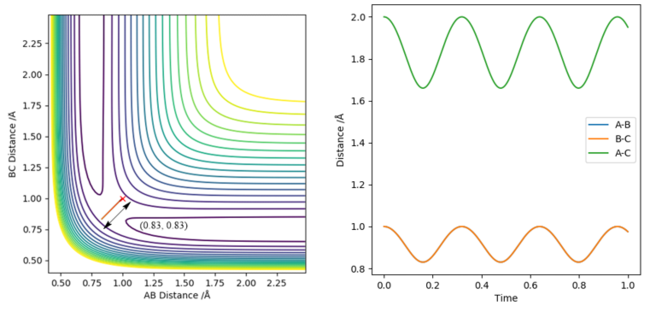
Figure 1 - (Left) Contour plot for H + H₂ system
Figure 2 - (Right) Heavy oscillation for Internuclear Displacement plot for H + H₂ system at R_{H_BH_C} = 0.83 Å

In addition, using 0.907742 Å as the input gave a non-oscillatory motion and showed a stationary particle, which is a feature of the transition state. Its energy also did not fluctuate with time.

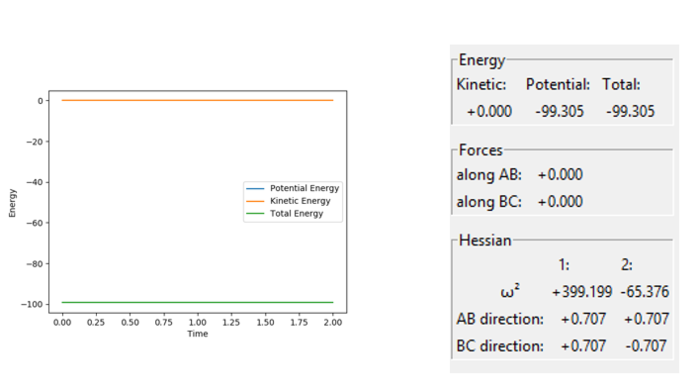
Figure 3 - (Left) Energy vs time plot for H + H₂ system, fluctuation of energy is zero, indicating a stationary point.
Figure 4 - (Right) GUI showing '0' Force and a negative eigenvalue and positive eigenvalue for H + H₂ system at R_{H_BH_C} = R_{H_AH_B} = 0.907742 Å

The GUI in figure 4 shows conclusively that it is indeed a saddle point. The eigenvalues of the Hessian matrix feature both a positive value: +399.199 and a negative value -65.376, an indicator of a saddle point since both maxima and minima are present.

Figure 5(a) - Graphical illustration of a saddle point: does not oscillate in the surface plot. Stays stationary.

Figure 5(b) - Graphical illustration of a saddle point: does not oscillate in the contour plot. The direction of eigenvectors shown, pointing in the direction of maxima and minima at the saddle point.

Ng611 (talk) 11:50, 22 May 2019 (BST) Again, excellent answer!

MEP and Dynamic Trajectory

Minimum Energy Path (MEP) refers to the lowest energy reaction pathway possible that still leads to product formation. ^[3] It reflects an infinitely slow motion where the momenta is reset to 0 in each step. The reaction coordinate at the saddle point reflects the direction of the unstable mode with the negative eigenvalue. Following the negative gradient of the PES surface that is concave downwards, one can trace out the MEP.

Comparison Between MEP and Dynamic Calculations

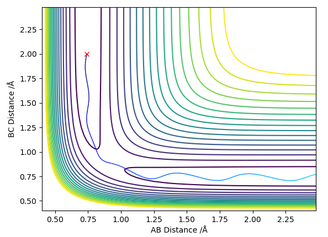
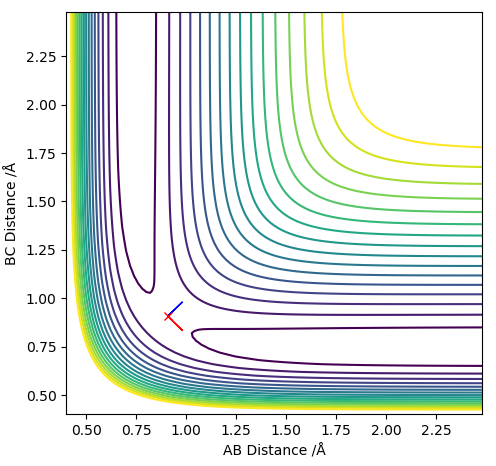
Next, the initial conditions of the system used were slightly modified, using MEP calculation to plot the trajectory using R_{H_AH_B} = 0.917742 Å and R_{H_BH_C} = 0.907742 Å.

The results of this calculation were compared to a dynamic calculation. Both dynamic and MEP show that R_{H_BH_C} approaches infinity with time, and R_{H_AH_B} fell to around 0.74 Å after being slightly perturbed from the transition state. This is because the slight perturbation causes H_A and H_B to be attracted to each other to form an H-H bond, while the remaing H_C is repelled away to infinity.

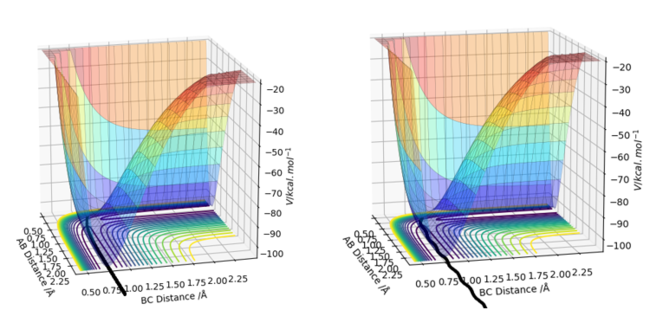
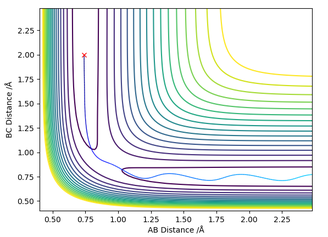
Figure 6 - (Left) Surface plot for H + H₂ system using MEP calculations
Figure 7 - (Right) Surface plot for H + H₂ system using dynamic calculations

The main difference between MEP and dynamic calculations is that oscillatory motion is present in dynamic calculations (which is more realistic, since real molecules possess internal energy after collisions that lead to vibration), but absent in MEP calculations. Oscillatory motion is absent in MEP since the MEP travels only along the minimal energy pathway, which avoids slight displacements into valleys of high potential energy that triggers oscillatory motion. The oscillatory motion in dynamic calculations can be observed from the internuclear distance vs time and contour plots. In dynamic calculations, on the other hand, the inertia of the atoms causes them to oscillate after encountering a valley of higher potential energy.

Internuclear Distance against Time Plot

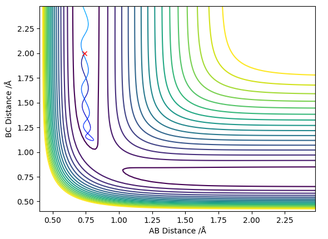
For the dynamic trajectory, the final distances are R_{H_BH_C} approximately 0.756 - 0.723 Å indicating formation of A H-H bond. The final distance of R_{H_AH_B} is 10 as the H_C is ejected away after the collision. For the MEP trajectory, the final distances are similar (with the exception of R_{H_BH_C} = 0.756 Å lacking oscillatory behaviour. This absence of oscillatory behaviour is due to the definition of MEP which resets the kinetic energy to zero, preventing oscillation along the regions which are not minimal energy pathways.

Another noteworthy difference in the Internuclear distance against time plot is that the distances of R_{H_AH_B} increases 'logarithmically' for MEP but linearly for dynamics calculation. This could be due to MEP's preference to move only along the lowest energy pathway, whereas dynamic calculations have no such preference. MEP removes kinetic energy from the system, which might have caused a non-linear increase in distances.

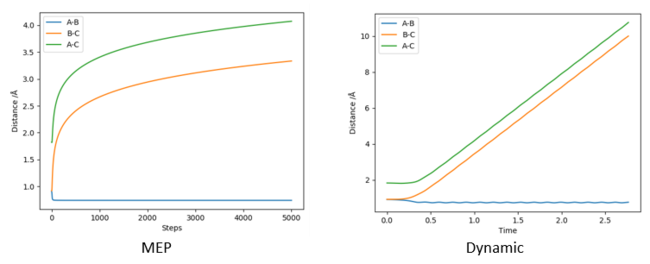
Figure 8 - (Left) Internuclear plot for H + H₂ system using MEP calculations
Figure 9 - (Right) Internuclear plot for H + H₂ system using dynamic calculations

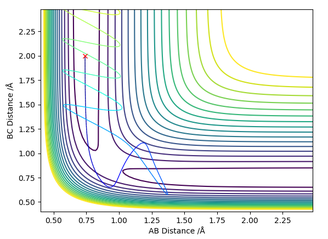
Reactive and Unreactive Trajectories for H₂

The initial conditions for this investigation would be R_{H_AH_B} = 0.74 Å, R_{H_BH_C} = 2.0 Å, with p_{H_AH_B} = p₁ and p_{H_BH_C} = p₂ which are varied as shown in Table 1.

Table 1
p₁	p₂	E_tot	Reactivity & Description
-1.25	-2.5	-99.018	Case 1. Reactive pathway. Reaction pathway led to product formation from H_AH_B + H_C to H_A + H_BH_C, equilibrium bond length seen obsrved for R_{H_BH_C}. Oscillatory motion of H_BH_C is observed after the reaction, and H_A is ejected.
-1.5	-2.0	-100.456	Case 2. Unreactive pathway. Kinetic energy insufficient for reaction, reaction barrier is not overcame, and particle does not form H₂. H_C is rebound after failing to cross the activation energy barrier.
-1.5	-2.5	-98.956	Case 3. Reactive pathway. Reaction pathway led to product formation for BC, equilibrium bond length seen. Vibration after reaction.
-2.5	-5.0	-84.956	Case 4. Unreactive pathway. Although reactive initially, high vibrational energy causes the Hydrogen atoms to bounce back and separate to reform the reactants. Hence, products are not seen.
-2.5	-5.2	-83.416	Case 5. Reactive pathway. Reactants form a product with high vibrational energy, due to their high initial kinetic energy. Product is vibrationally excited.

As seen in table 1, the assumption that a molecule possessing energy larger than the activation energy barrier can react is not always true. In the fourth case, even when the momentum of p₁ and p₂ were high, reaction did not necessarily occur. In contrast, reactions can occur for lower energy systems as seen in cases 1 and 3.

Transition State Theory

Transition rate theory (TST) is a model that accounts for chemical reaction rates by considering the mechanistic interactions between the reactants, transition states, and products. ^[4]

1) Atoms in the reactant state are Boltzmann distributed.

2) Once the reactant crosses the activation energy barrier, it will form the product and not reform the starting reactant again.

3) Particles behave classically, and quantum phenomena such as quantum tunneling are not anticipated.

4) The reactants are in equilibrium with the activated complex.

5) The Born-Oppenheimer approximation holds in this model

The main limitation of TST in this investigation is assumption 2) and 3): That the particles behave classically, and that once a particle crosses the activation energy barrier, no reaction occurs. The simulation in case 4 shows the flaws of such an assumption as the particles can 'bounce-back' to form the reactants due to the high vibrational energy present even though it has already crossed the transition state and activation energy barrier. This phenomenon of barrier re-crossing is not considered by TST.

When Energy is higher than activation energy barrier, TST predicts successful reaction when in fact, we know from our simulation this is not necessarily the case due to re-crossing. Predicted rates here are higher than the experimental values observed.

The second phenomena ignored by TST is quantum tunneling, which can occur for low activation energy barriers. When energy is lower than activation energy barrier, TST predicts that the reactants would not be able to form products, when in fact, tunneling can occur for low activation energy reactions and lead to product formation. This is not predicted by TST model, causing the predicted rate to be smaller than observed when the reactants have low energy. ^[5]

Ng611 (talk) 11:56, 22 May 2019 (BST) Excellent answer! In essence, you have two competing effects, tunnelling and TS recrossing, which affect the reaction rate in different ways. Which effect dominates is a tough question and probably needs to be determined experimentally

Excercise 2: F - H - H System

PES Inspection

F + H₂ and H + HF reaction energetics

H₂ + F -> HF + H is an exothermic reaction as energy is released from this reaction. Fluorine, the most electronegative element has an attractive PES slope (valley) that attracts the H₂ molecule towards it. This can be seen from the trajectory of the reaction on the contour plot. The Hydrogen molecule gains kinetic energy and is from the fall in potential energy moving from the H-H bond to the H-F bond. This is because the H-H bond is 436 kJ/mol ^[6], weaker than the H-F bond strength of 565 kJ/mol. ^[7] The energetics of the reaction is related to the strength of the bonds formed compared to the strength of the bonds broken. Since the H-F bond formed is stronger than the H-H bond broken, the reaction is exothermic. Another indicator of the energetics of the reaction would be the PES shown in figures 11 and 13. The reactants are seen to be at higher potential energy than the products, which is a sign that the reaction will lose potential energy, and is exothermic.

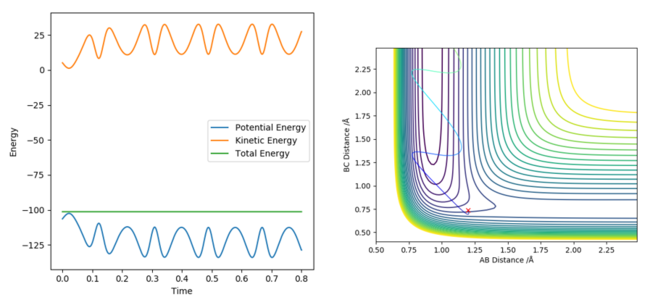
Figure 10 - (Left) Energy plot for F + H₂ system using dynamic calculations
Figure 11 - (Right) Contour plot for F + H₂ showing the PES and the attractive nature of the region surrounding Fluorine

Approximate Position of Transition State

Hammond's postulate states that the transition state of a reaction resembles the reactants or the products depending on which one it lies closer to energetically. For an exothermic reaction like H₂ + F -> HF + H, the reactants lie closer energetically to the transition state of the reaction than the products. Hence, the transition state for this reaction: [H-H-F]^‡ complex should resemble the reactants and its geometries. By approximating the H-H bond in the transition state to remain approximately constant, the H-F bond length was adjusted until approximately '0' force was attained in the GUI, along with a positive and negative eigenvalue. The H-F bond length of the transition state was found to be 1.8103 Å and the H-H bond length was approximated as 0.74489 Å.

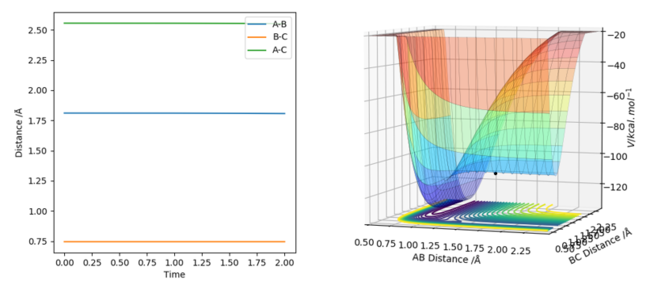
Figure 12 - (Left) Internuclear Distance vs Time plot for F + H₂ revealing the stationary nature of saddle point where the transition state is stationary
Figure 13 - (Right) Surface plot for F + H₂ showing the stationary saddle point of the transition state

Calculating activation energies

The activation energy is given by the difference in energy between the transition state and the reactants. This can be found by slightly perturbing the transition state either in the direction of the forward or backward reaction and estimating assuming that the product will be formed at long time intervals.

Initial Conditions for the forward reaction: R_HF = 1.8301 Å, R_HH = 0.7463 Å.

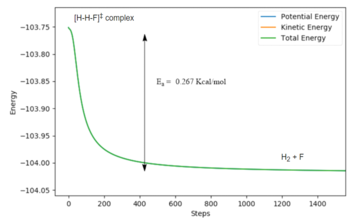
Figure 14: The activation energy for the forward reaction determined by slightly perturbating it in direction of reverse reaction

For the forward reaction H₂ + F -> HF + H: Activation Energy = -103.751 -(-104.018) = 0.267 kcal/mol. This is close to literature values for the activation energy of 0.3 kcal/mol. ^[8]

Initial Conditions for the reverse reaction: R_HF = 1.8065 Å, R_HH = 0.7447 Å .

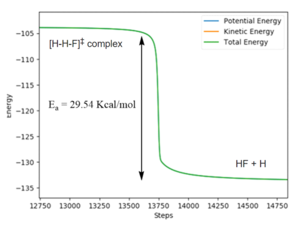
Figure 15: The activation energy for the reverse reaction determined by slightly perturbating it in direction of forward reaction

For the reverse HF + H reaction: Activation Energy: -103.87 -(-133.41) = 29.54 kcal/mol

The higher activation energy for the reverse reaction compared to the activation energy of the forward reaction is a sign that the reaction is exothermic. Subtracting the reverse reaction activation energy from the forward reaction activation energy gives the energy change of the forward reaction.

ΔE = 0.267 - 29.54 = -29.3 kcal/mol

This value is reasonably close to the enthalpy change reported by Polanyi and co.: -31.5 kcal/mol ^[9]. The deviations in activation energies and enthalpy change is likely due to the fact that the system has been arbitrarily perturbed a small distance away from the transition state, and this small distance could have led to deviation in energy from the energy of the transition state. It could also be due to the limitations of the approximations and theories used in this LEPS (London-Eyring-Polanyi-Sato) model.

Ng611 (talk) 11:58, 22 May 2019 (BST)Good answer! A minor note on style, I would use "et al." instead of "and co", as et al. is the standard way of writing this.

Reaction Dynamics

Mechanism for the release of reactive energy

Initial Conditions for investigating reaction parameters. R_HF: 1.81 Å, R_HH distance: 0.74 Å. p_HF and p_HH are set to be 0.

The H₂ molecule travels in a relatively straight projectile initially, with little vibration. After the Collision with F in the attractive potential surface, the newly formed HF molecule hits a steep wall of the valley of the PES and becomes vibrationally excited with excess kinetic energy from the exothermic reaction.

This might be observed with spectroscopic or calorimetric techniques to detect the IR radiation emitted after de-excitation. Spectroscopic techniques may be able to detect emissions when vibrationally excited states decay, and if the vibrational states involved in spectroscopic measurements feature changes in dipole moment (To satisfy gross selection rule) to be detectable. Polanyi and co. have used infrared chemiluminescence to measure the rotational, vibrational and translational energies of the products of the exothermic reaction to match experimental rate constants and activation energies to the values determined by dynamic calculations. ^[10]

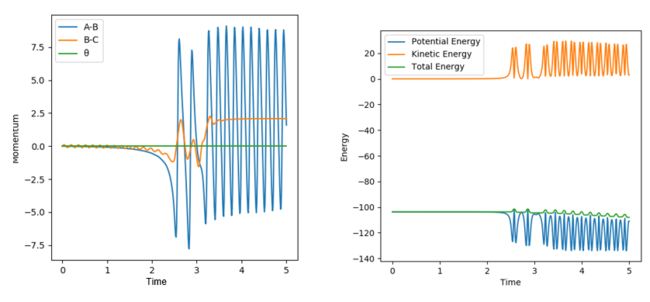
Figure 16 - (Left) Momentum vs Time plot for F + H₂. Note the increase in momentum after exothermic reaction
Figure 17 - (Right) Energy vs Time plot for F + H₂ showing the oscillatory behaviour of the vibrationally excited products after reaction

For Calorimetry, when an exothermic reaction occurs, the enthalpy change can be detected as heat changes using set-up like Bomb Calorimeters to monitor the thermodynamics of the reaction. ^[11]

Ng611 (talk) 11:59, 22 May 2019 (BST) Excellent!

Polanyi's Rules

Polanyi's Rules state that vibrational excitation favours the reaction if the reaction is endothermic. (late TS along the reaction pathway according to Hammond's Postulate) and translational energy inhibits the reaction if the reaction is exothermic (early TS along the reaction pathway according to Hammond's Postulate). ^[12] Intuitively, one might think that higher vibrational excitation favours a reaction by providing excess kinetic energy to overcome the reaction barrier. However, in the case of H₂, the opposite can happen as demonstrated in the simulation below.

Simulation 1:

H₂ + F -> HF Forward Reaction

R_HH = 0.74 Å, R_HF = 1.8065 Å, p_FH = -0.5, p_HH = -2.99

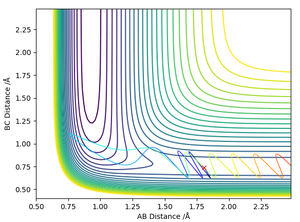
The Simulation showed that the excited vibrational states hindered the forward exothermic reaction as anticipated by Polanyi's Rules. The PES reveals that the product region is attractive (due to the lower potential of electronegative fluorine), as indicated by the contours that attract the H₂ molecule. This attractive region attracts the reactants to form the products. This is likely due to the oscillatory motion causing the molecule to hit a region of high repulsive energy along the PES valley causing repulsion of the reactants back away from the activation energy barrier. This prevents the forward reaction.

Simulation 2:

H₂ + F -> HF Forward Reaction

R_HH = 0.74 Å, R_HF = 1.8065 Å, p_FH = -0.8, p_HH = -0.1

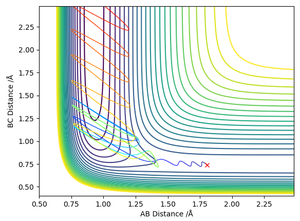
A successful reaction has now occurred, the lower vibrational energy has actually aided reaction, by allowing the H₂ molecule to smoothly pass through the activation energy barrier and prevented the excessive vibrational energy from causing reformation of the starting reagents. Worth noting the vibrationally excited product formed after a successful exothermic reaction.

Simulation 3:

HF -> H₂ + F Reverse Reaction

R_HF = 0.91996 Å, R_HH = 2.0000 Å, p_FH = 0.1, p_HH = -3

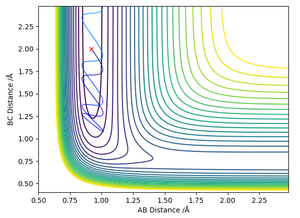
The reaction is unsuccessful due to the low vibrational energy of the reactants, and they lack the kinetic energy to surmount the activation energy barrier.

Simulation 4:

HF -> H₂ + F Reverse Reaction

R_HF = 0.91996 Å, R_HH = 2.0000 Å, p_FH = 8, p_HH = -0.1

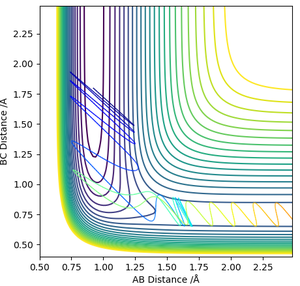
In the reverse endothermic reaction, the PES surface would be reversed, where the products will have higher potential energy and is now a repulsive field. The additional vibrational energy in Simulation 1 which hindered the forward exothermic reaction would prove to be useful for climbing the slope of the high activation energy barrier. This is because the oscillation is now hitting the high energy valleys of the PES, allowing it to surmount the activation energy barrier and pass the saddle point to form products. The products will now be de-excited vibrationally compared to the reactants.

The 4 simulations illustrate Polanyi's Rules for late and early TS.

Ng611 (talk) 12:00, 22 May 2019 (BST) Great answer!

Bibliography

↑ G. Thomas, R. Finney and M. Weir, Calculus and analytic geometry, Addison-Wesley, Boston, 2003.
↑ G. Strang and K. Borre, Linear algebra, geodesy, and GPS, Wellesley-Cambridge Press, Wellesley, Mass., 1997.
↑ D. Sheppard, R. Terrell and G. Henkelman, The Journal of Chemical Physics, 2008, 128, 134106.
↑ D. Truhular, W. Hase and J. Hynes, Chemischer Informationsdienst, 1983, 14.
↑ I. Levine and I. Levine, Physical Chemistry, McGraw-Hill, New York, 2008.
↑ P. Atkins and J. De Paula, Atkins' Physical chemistry, Oxford University Press, Oxford, 2006.
↑ P. Atkins and J. De Paula, Atkins' Physical chemistry, Oxford University Press, Oxford, 2006.
↑ D. Truhlar, B. Garrett and N. Blais, The Journal of Chemical Physics, 1984, 80, 232-240.
↑ J. Polanyi and K. Woodall, The Journal of Chemical Physics, 1972, 57, 1574-1586.
↑ J. Polanyi and K. Woodall, The Journal of Chemical Physics, 1972, 57, 1574-1586.
↑ P. Atkins and J. De Paula, Atkins' Physical chemistry, Oxford University Press, Oxford, 2006.
↑ P. Atkins and J. De Paula, Atkins' Physical chemistry, Oxford University Press, Oxford, 2006.

[1] G. Thomas, R. Finney and M. Weir, Calculus and analytic geometry, Addison-Wesley, Boston, 2003.

[2] G. Strang and K. Borre, Linear algebra, geodesy, and GPS, Wellesley-Cambridge Press, Wellesley, Mass., 1997.

[3] D. Sheppard, R. Terrell and G. Henkelman, The Journal of Chemical Physics, 2008, 128, 134106.

[4] D. Truhular, W. Hase and J. Hynes, Chemischer Informationsdienst, 1983, 14.

[5] I. Levine and I. Levine, Physical Chemistry, McGraw-Hill, New York, 2008.

[6] P. Atkins and J. De Paula, Atkins' Physical chemistry, Oxford University Press, Oxford, 2006.

[7] P. Atkins and J. De Paula, Atkins' Physical chemistry, Oxford University Press, Oxford, 2006.

[8] D. Truhlar, B. Garrett and N. Blais, The Journal of Chemical Physics, 1984, 80, 232-240.

[9] J. Polanyi and K. Woodall, The Journal of Chemical Physics, 1972, 57, 1574-1586.

[10] J. Polanyi and K. Woodall, The Journal of Chemical Physics, 1972, 57, 1574-1586.

[11] P. Atkins and J. De Paula, Atkins' Physical chemistry, Oxford University Press, Oxford, 2006.

[12] P. Atkins and J. De Paula, Atkins' Physical chemistry, Oxford University Press, Oxford, 2006.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

Exercise 1: H + H2 System

Transition State

Estimation of the Transition state

MEP and Dynamic Trajectory

Comparison Between MEP and Dynamic Calculations

Internuclear Distance against Time Plot

Reactive and Unreactive Trajectories for H2

Transition State Theory

Excercise 2: F - H - H System

PES Inspection

F + H2 and H + HF reaction energetics

Approximate Position of Transition State

Calculating activation energies

Reaction Dynamics

Mechanism for the release of reactive energy

Polanyi's Rules

Bibliography

Exercise 1: H + H₂ System

Reactive and Unreactive Trajectories for H₂

F + H₂ and H + HF reaction energetics