MRD:01089606
Exercise 1
Qn 1. What value does the total gradient of the potential energy surface have at a minimum and at a transition structure? Briefly explain how minima and transition structures can be distinguished using the curvature of the potential energy surface.
At the minima and transition structure, the total gradient is 0. The transition state is a maximum point (second derivative is negative) and upon a small change in r1 or r2, the trajectory will change towards the direction of the products/ reactants. It will be displayed on the potential energy surface as a hill. However, the minima (second derivative is positive) will be displayed as a well in the surface, and a small change in r1 or r2 will not move the trajectory by much as the surrounding surfaces have a higher potential energy.
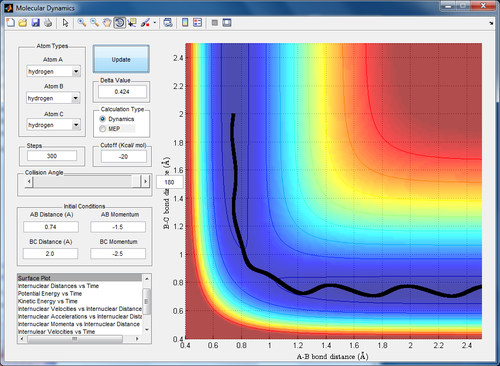
Qn 2. Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” screenshot for a relevant trajectory.
Transition state position = 0.907 A
This point is the intersection of the maxima and minima of the potential graph at multiple values of r1/r2. At the transition state, there is temporarily zero force acting on the atoms and the atoms are temporarily at rest. Hence, at this point, there is no vibration of the atoms and the graph of internuclear distance vs time shows 2 straight lines. The difference between these 2 lines gives the same value for the transition state position.

Qn 3. Comment on how the mep and the trajectory you just calculated differ.
The reaction path shown by the mep is very straight while the trajectory in dynamics is more wavy. This is because the mep assumes that the atoms have no mass and infinitely slow motion and hence, have less vibration in their movement. This is not assumed in the dynamic calculation and hence, the line shows vibration as the molecules move towards the transition state.
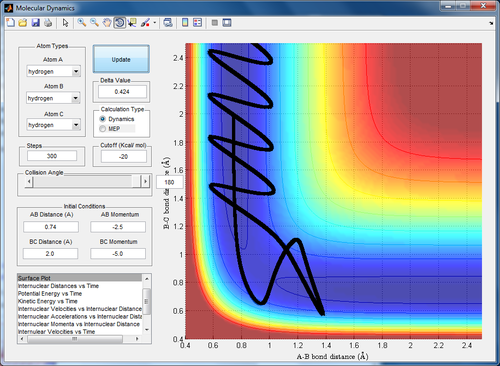
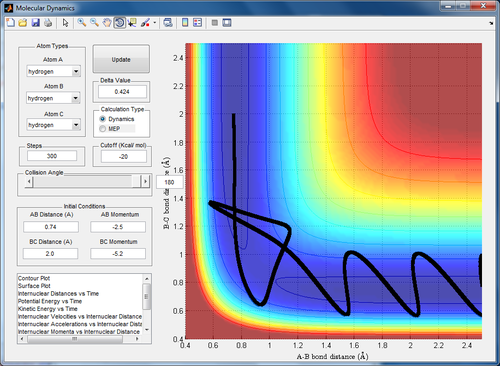
Qn 4. Complete the table by adding a column reporting if the trajectory is reactive or unreactive. For each set of initial conditions, provide a screenshot of the trajectory and a small description for what happens along the trajectory.
| p1 | p2 | Trajectory |
|---|---|---|
| -1.25 | -2.5 | -Reactive |
| -1.5 | -2.0 | Unreactive |
| -1.5 | -2.5 | Reactive |
| -2.5 | -5.0 | Unreactive |
| -2.5 | -5.2 | Reactive |
For case 1,
The H1 atom approaches the H2-H3 molecule. This causes a bond to form between H1-H2 and the bond between H2-H3 to break at the transition state. The H3 atom then moves off in the opposite direction.
For case 2,
The H1 atom has insufficient initial momentum to get close enough to the H2-H3 molecule to form a bond with H2. Hence, the H2-H3 molecule remains intact and the H1 atom simply returns to its original reactant position.
For case 3,
With this slight increase in momentum of the H1 atom, the atom now approaches the H2-H3 molecule until the transition state position is reached. The H3 atom moves off in the opposite direction.
For case 4,
The H1 atom approaches the molecule. In this case, it is clear that the reactants never cross the transition state. However, they are still able to form the products momentarily via a different pathway. The system does not have sufficient energy to remain in the product state and thus reverts back to the reactant forms.
For case 5,
The H1 atom approaches the molecule and again without crossing the transition state, forms a bond with H2. AT the same time, the bond H2-H3 breaks. There is a point where the H1-H2 bond begins to break and the system returns to the reactant side but ultimately, the system stays in the final products state of H3 and H1-H2.
Qn 5. State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?
1. Each intermediate has a long enough half-life to reach a boltzmann distribution of energy before continuing on to the next step.
2. Atomic nuclei behave according to classic mechanics. If the reactants and products do not collide with enough energy to reach the transition state, the reaction will not occur.
3. The reactants will pass through the transition state which is the saddle point on the potential energy surface.
4. The transition state is in equilibrium with the reactants and products.
5. The forward rate of reaction is independent of the backward reaction rate.
Transition state theory fails to explain why there are successful reactions that do not go past the transition state. This is the breaking down of assumption 3 since not all successful reaction pathways have to pass through the transition state. The TS theory also fails to explain why there are some reaction pathways that show the reactants forming products momentarily only to reform the reactants.This may be explained by the assumption 4 breaking down. The reactants and products may not be in equilibrium, which could explain why when some product is formed the backward reaction becomes favoured and the system reverts back to the reactant system.
The TS theory predictions for reaction rate values will be lower than experimental values based on assumptions 2 and 3. TS theory fails to account for successive reactions via quantum tunnelling which is possible if the reactants are treated quantum mechanically. Furthermore, TS theory fails to account for the reactions that are successful even without crossing the transition state saddle point. These reactions do occur as seen in the 5th case shown above.
Exercise 2
Qn 1. Classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?
Based on the curvature of the potential energy surface, it is possible to identify whether the reactants for each reaction have more or less energy than the products and classify them according to their energetics.
| F + H2 | Exothermic |
| H + HF | Endothermic |
The enthalpy of reaction is given by the enthalpy of products minus the enthalpy of reactants. In the case of F + H2, the enthalpy of reaction is negative since the reaction is exothermic. This tells us the products are more stable than the reactants and the H-F bond strength is greater than the H-H bond strength.
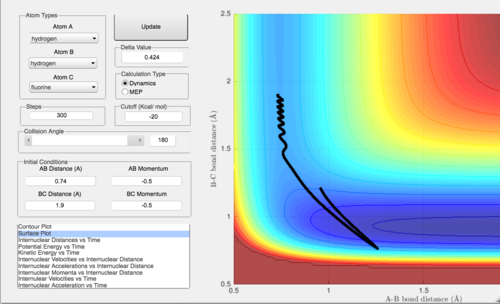
Qn 2. Locate the approximate position of the transition state.
At the transition state, there is no net force acting on the molecule. Hence, the molecule should not move in any direction when there is 0 momentum applied to the system. The initial conditions were varied for the forward reaction until this point was found. This occurs at H-H distance = 0.74 A and H-F distance = 1.815 A.
Qn 3. Report the activation energy for both reactions.
For the reaction F + H2, activation energy = -103.7416-(-103.9313)= 0.1897 kcal/mol
For the reaction H + HF, activation energy = -103.7416-(-133.6446)= 29.90 kcal/mol
Qn 4. In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. How could this be confirmed experimentally?
For energy to be conserved, the total energy (kinetic and potential) of the system will remain the same in the reactants and products states. The reactants have a higher potential energy than the products since this is an exothermic reaction. Hence, to ensure energy is conserved, the reactants have a lower kinetic energy than the products. This is shown in the graph of kinetic energy against time, where there is an absolute increase in kinetic energy from reactants (H2) to products (HF).
Since the products' kinetic energy show a wave pattern, we know that the products contain a large amount of vibrational energy. This can be experimentally proven using FTIR techniques, as the product spectrum will contain a H-F vibrational peak. There will be no peak initially as the H2 molecule has 0 net dipole. This vibrational energy can also be lost through vibrational relaxation, emitting a photon. Hence, the trajectory of this reaction can be proven to be reactive if there is an increase in photon emission as measured by a photon detector.
Qn 5. Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.
The efficiency of the reaction is affected by the translational and vibrational energy of the reactants. In order for the reaction to occur efficiently, the reactants must have sufficient translation energy to approach each other to a close enough distance to form the transition state. However, the vibrational energy in the molecule will also affect the efficiency of the reaction. Depending on the vibrational mode the molecule is in when the incoming atom collides with it, the reaction will be successful and the products will form or the reaction will be unsuccessful and the reactants will reform after the transition state.
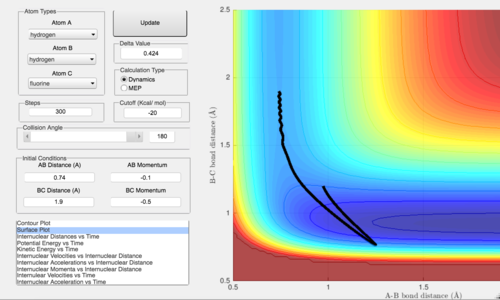
In the first case, pFH = -0.5 while pHH is varied from -3 to 3. pHH tells us about the vibrational energy of the H2 molecule where a negative value indicates the molecules are coming together and a positive value that they are moving apart. It is found that when absolute value of pHH is greater, the molecule vibrates a lot before reaching the transition state. This means that a lot of energy is spent in the vibrational motion and does not help the reactants reach the transition state with sufficient energy to form the products.
Comparing the 3 trajectories above, when the energy of the H-H vibration is decreased, the motion of the reactants becomes less vibrational and the reactants are able to progress more into the reaction even with less energy in the system. This indicates the system is more efficient. As seen in the first trajectory, pHH is the highest at -2.7 but the reaction eventually goes back to the reactants side, indicating even with high vibrational energy, the reaction still might not take place if it not accompanied by the right amount of translational energy. As pHH is gradually reduced, the reaction remains on the product side but shows a slight inclination to return to the reactant side. By varying translational energy at this low vibrational energy level, it is possible to convert this translational energy of the reactants into the vibrational energy of the H-F bond, which would encourage the system to remain on the products side.
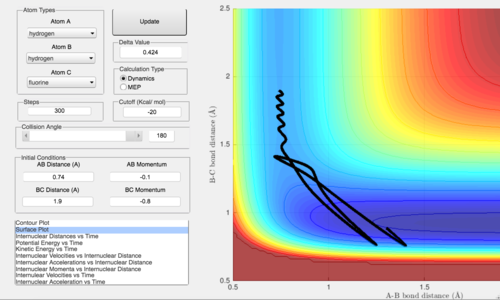
The trajectory above shows the momentum of the incoming F atom being increased to -0.8 while pHH is left at a low -0.1. It is found that this at this combination of vibrational and translational energy, the reaction is progressing more efficiently. There is little 'wastage' of energy as vibrational energy before the reactants cross the transition state and this energy is instead used to move the reactants towards the transition state. After the transition state is crossed, there is also vibrational energy in the H-F bond as seen from the wave like pattern in the products well. This vibrational energy makes the reaction more likely to progress towards the products instead of reverting to the reactants.
Now focusing on the reverse reaction, we can identify how the distribution of energy varies based on the position of the transition state. In the forward reaction, the transition state was early and the activation energy was smaller. Hence, reducing the energy of the system was ideal since the reaction would still happen even at low energies. In the backward reaction, the activation energy is almost 30 kcal/mol. Hence, the overall energy put into the system is much higher. This is done by greatly increasing the vibrational energy of the H-F bond and keeping the momentum of the incoming atom relatively high. Hence, the reactants have sufficient energy to overcome the activation barrier and reach the late transition state. The distribution of energy in the reverse reaction is also different from the forward reaction. Vibrational energy of the reactants is necessary as it combines with the translational energy from the momentum of the incoming atom to ensure the reaction can reach the transition state. If a low vibrational energy and higher translational energy model was used like before, the reactants would always remain in the reactant well as they are unable to cross the activation barrier.
References
- Anslyn, Eric V.; Doughtery, Dennis A., Transition State Theory and Related Topics. In Modern Physical Organic Chemistry University Science Books: 2006; pp 365–373
- Cleland, W.W., Isotope Effects: Determination of Enzyme Transition State Structure. Methods in Enzymology 1995, 249, 341-373
- Laidler, K.; King, C., Development of transition-state theory. The Journal of Physical Chemistry 1983, 87, (15), 2657
- Laidler, K., A lifetime of transition-state theory. The Chemical Intelligencer 1998, 4, (3), 39
- Radzicka, A.; Woldenden, R., Transition State and Multisubstrate$Analog Inhibitors. Methods in Enzymology 1995, 249, 284-312
- Schramm, VL., Enzymatic Transition States and Transition State Analog Design. Annual Review of Biochemistry 1998, 67, 693-720
- Schramm, V.L., Enzymatic Transition State Theory and Transition State Analogue Design. Journal of Biological Chemistry 2007, 282, (39), 28297-28300
- Chem. Sci., 2016, 7, 3992