MRD:01060479
Molecular Reaction Dynamics: Applications to Triatomic systems
Exercise 1: H + H2 system
Dynamics from the transition state region
What value does the total gradient of the potential energy surface have at a minimum and at a transition structure? Briefly explain how minima and transition structures can be distinguished using the curvature of the potential energy surface:
The total gradient at both the minimum and at the transition structure of the potential energy surface is equal to zero. A transition state is a maximum within the overall minimum energy pathway. Finding the second derivative of both points allows them to be distinguished, with the transition state having a second derivative less than zero and the minima having one greater than zero. These two points can be distinguished by observing the reaction trajectory at a point slightly greater or smaller than each. For the minima, the trajectory will return to the minima, meaning the reactants or products will be unchanged. However, a small change from the transition state will mean the trajectory rolls to the reactants or products.
Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” screenshot for a relevant trajectory.
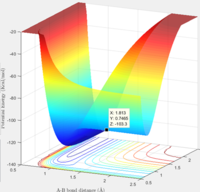
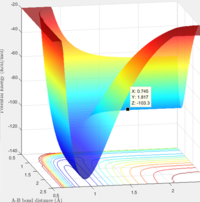
rts= 0.91
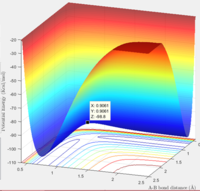
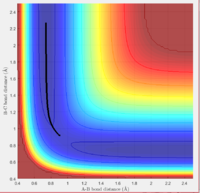

The surface plot image shows that the point rts=0.91 is the maximum point along the minimum energy path, corresponding to the transition state. The internuclear distances image shows that when A and B-C are present at this point, no reaction takes place. The trajectory is simply oscillating. The B-C and A-B bonds are oscillating on the ridge, and remaining fairly constant.
Calculating the reaction path
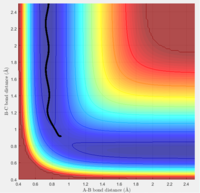
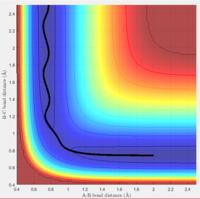
Trajectories from r1 = rts+δ, r2 = rts
Comment on how the mep and the trajectory you just calculated differ.
The minimum energy path and the dynamic trajectory follow a similar path for r1 = rts+δ, r2 = rts. This is to be expected, as the mep will give the lowest energy route possible. The dynamic trajectory shows how once the bond between A and B is formed, the molecule oscillates. This is because the mep trajectory resets the velocity to zero at each time step. Therefore, the previoius velocity of the molecule will not be taken into account, so the molecule will not experience inertial motion. This is not a realistic representation of the reaction.
The 'Internuclear distances vs Time' and 'Internuclear Momenta vs Time' were considered for this trajectory. The final values of r1(t) and r2(t) were 5.38 and 0.74 respectively, and the values of p1(t) and p2(t) at large t were 2.48 and 1.23 respectively.
A different trajectory was then tested, with r2 = rts+δ and r1 = rts. The final values for internuclear distances and momenta for large t values were identical, but reversed, with the value of p1 equal to p2 and vice versa, the same applied to distance. This result was to be expected, as this small displacement from the transition state lead to the trajectory rolling down the opposite direction, towards the reactants.
Reactive and Unreactive Trajectories
| p1 | p2 | Reactive/Unreactive |
|---|---|---|
| -1.25 | -2.5 | Reactive |
| -1.5 | -2.0 | Unreactive |
| -1.5 | -2.5 | Reactive |
| -2.5 | -5.0 | Unreactive |
| -2.5 | -5.2 | Reactive |
Complete the table by adding a column reporting if the trajectory is reactive or unreactive. For each set of initial conditions, provide a screenshot of the trajectory and a small description for what happens along the trajectory
Reactive and Unreactive Trajectories
1. The A-B bond distance decreases as the A approaches B-C, due to A's higher momentum in the negative direction. The kinetic energy is sufficient to overcome the activation barrier, so the trajectory is reactive, and reverts to the products. The newly formed A-B bond then oscillates as the C atom moves away.
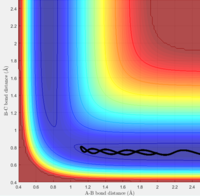
2. The A-B bond distance decreases as the A approaches B-C, but the momentum of both are lower, so the kinetic energy is not sufficient to overcome the activation barrier. Therefore the trajectory is unreactive, and the trajectory reverts to the reactants. The A-B bond distance returns to its normal length and continues to oscillate.
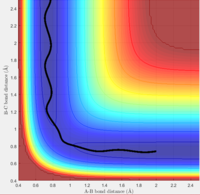
3. This trajectory is very similar to the first, where p1=-1.25 and p2=-2.5. The only difference is that the B-C bond slightly oscillates before the transition state is reached. This can attributed to the A-B molecule containing more vibrational energy, from the increased momentum.

4. This trajectory once again begins with A approaching B-C, this time with much greater momentum. Once the transition state is reached, the distance between A and B decreases as a bond between them is formed. However, the trajectory then changes, with the B-C bond being formed again and A and B separating, reverting back to the reactants. This is barrier recrossing, and the trajectory is unreactive.
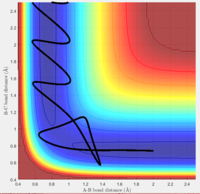
5. This trajectory has similar initial conditions that the fourth trajectory. The bond is formed between A and B, and then reverts back to the separated reactants. However, instead of barrier recrossing, the bond between and A and B is formed once again, instead of simple barrier recrossing. This can be attributed to the slightly greater initial momentum in the A atom The A-B bond then oscillates vigorously and the trajectory goes to the products. This is a reactive trajectory.
Transition State Theory
Assumptions
- Based only on classical mechanics, rather than quantum mechanics. The assumption is that if the two reactants do not have enough energy to overcome the potential energy barrier, the reaction will not take place. However, this theory does not factor in the possibility of reactants tunnelling through the finite potential barrier1.
Therefore, with these assumptions taken into account, the Transition State Theory will give a lower reaction rate than the experimental values found, as the presence of tunnelling will increase the rate of the reaction.
EXERCISE 2: F - H - H system
F + H2 to H + HF
The reaction is exothermic, as the products have lower potential energy than the products. The products are more stable than the reactants, indicating that the bond strength of the H-F bond must be greater than that of the H-H bond. Hammond's postulate suggests that the transition state should closely resemble the reactants. The activation energy for this reaction is approximately 0 Kcal/mol.
Transition State= r1= 0.75, r2= 1.81 Activation Energy= 0 Kcal/mol
H + HF to H2 + F
The reaction is endothermic, as the products have higher potential energy than the products. The products are less stable than the reactants, indicating once again that the bond strength of the H-F bond must be greater than that of the H-H bond.
Transition State= r1= 1.81, r2= 0.75 Activation Energy= 30.7 Kcal/mol
Reaction Dynamics
Reactive trajectory for F + H2: Initial Conditions - r1= 0.75, r2=1.81, p1=-0.5, p2=-2.5
In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. How could this be confirmed experimentally?

Because of the reaction being exothermic, the potential energy gained from the conversion of reactants to products must be either stored or released in order for conservation of energy to be obeyed. It appears that this energy is stored in the product as vibrational energy. This can be seen from the large oscillations that can be seen on the reactive trajectory in the image to the right. The This could be confirmed by observing the reaction spectroscopically. One of these techniques involves the use of femtosecond laser pulses to record absorbances2. This vibrational mode will have very large oscillations, so its absorbance should be easy to identify.
Exploring values of pHH
H2 + F reaction
- When pHH equals 3,the H-H bond vibrates vigorously, due to the large amount of energy present due to the high momentum. However, the trajectory is not reactive, as the H-F bond starts to form, but then reverts back to the reactants. - When pHH equals -3, the trajectory is almost identical to when pHH= 3. - An intermediate value where pHH=0 gives a trajectory where the H-H bond will oscillate, and the distance between H and F will increase as the F atom moves further away.
-When pFH=-0.8 and pHH=0.1, the trajectory is reactive, giving a H-F molecule that oscillates rapidly.
H + HF reaction
Initial conditions: pHF= 0, pHH=-5 eg. a H atom colliding with high kinetic energy with HF -The reaction does not take place, the trajectory is non reactive.
A reactive trajectory can be found when pHF=10 and pHH=-0.1, corresponding to a greater vibration for the H-F bond and a smaller momentum for the incoming H atom.

Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.
Polanyi's empirical rules describe that if the transition state, or barrier, resembles the reactants more than the products, the reaction will be more efficient if the barrier is overcome by motion along the translational degree of freedom. If the transition state resembles the products, then the barrier will be more effectively overcome by motion along the vibrational degree of freedom3. This rule is supported by the examination of the two reactions above. For the exothermic F + H2 reaction, when H2 had low vibrational energy but F had high translational energy, the reaction took place. The opposite was the case when examining the HF + F reaction.
References
1. Eyring, H., J. Chem. Phys. 1935, 3 (2): 107–115
2. Atkins, P. W., & De, P. J., Atkins' Physical chemistry, 2006. Oxford: Oxford University Press, p182
3. Polanyi, J. C. Concepts in Reaction Dynamics. Acc. Chem. Res.1972, 5, 161−168
