MRD:01058157
Transition States on a Potential Energy Surface for Hydrogen Exchange Reaction
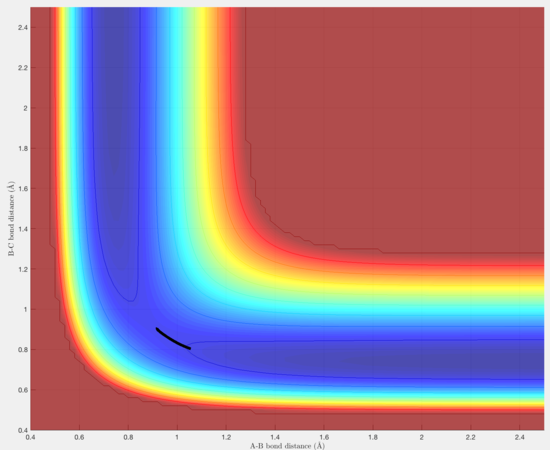
Locating the transition state
The total gradient of the potential energy surface is zero at both the minima and the transition state - saddle points. These points on the potential energy surface can be distinguished by considering the second derivative of the potential energy surface: the transition state is indicated by a negative curvature and the minima by a positive curvature.
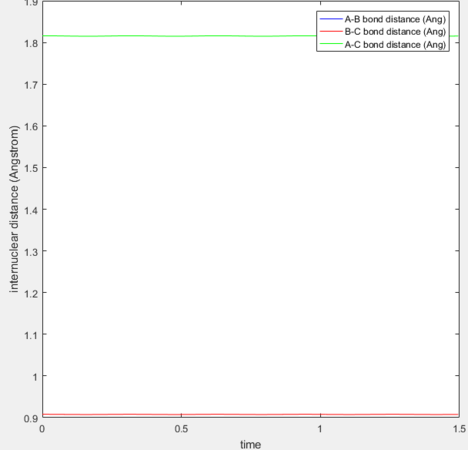
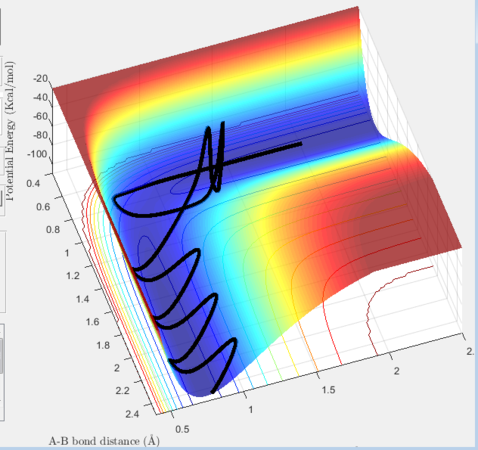
The transition state for the reaction H + H2 → H2 + H was located by setting the initial momentum for both species to 0 and equating the internuclear distances (r1 and r2) between the outer and central hydrogen, as when r1=r2=rts. No oscillation is observed as the reactants remain on the transition state ridge. The transition state position occurs at (0.908, 0.908).
Comparing Reaction Trajectories
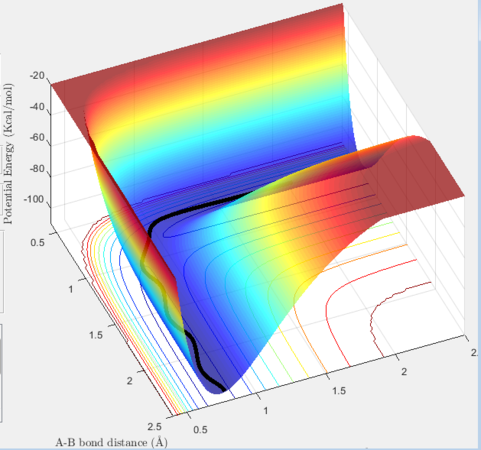
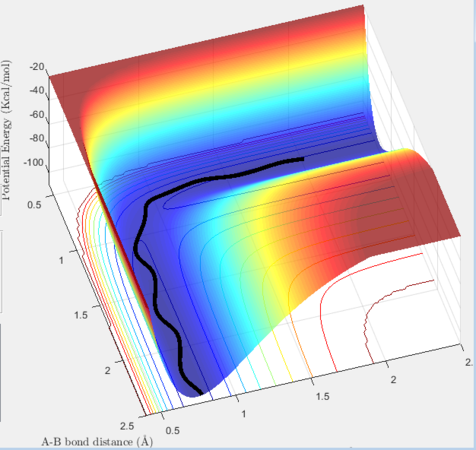
The simulation also examines the minimum energy path (mep), which treats the reacting particles as having infinitely slow motion. Hence the reaction trajectory follows the lowest path in the potential well displaying no vibrational tendencies. Here, the trajectory was studied with an initial momentum of 0 and one of the atoms slightly displaced from the transition state radius (+0.01). This was contrasted with dynamic trajectory for the same condition, which incorporates lateral movement along the potential energy surface.
The side-by-side comparison heightens the contrast between the two reaction trajectories. As the minimum energy paths follows most stable trajectory from reactants to product the gradient of the path is 0. It begins at the the transition state and falls slowly down the potential surface. In comparison, in the dynamic state, the HF species has vibrational energy which displaces it back to the reactants from the starting transition state due to interconverting between the energies, allowing it to collapse more rapidly. However, it also follows the general minimum energy path, only with additional vibrational motion.
Reactive and Unreactive Trajectories
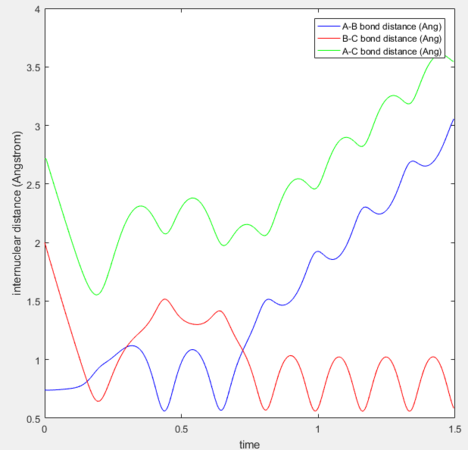
p1= -1.25, p= -2.5 Reaction Successful
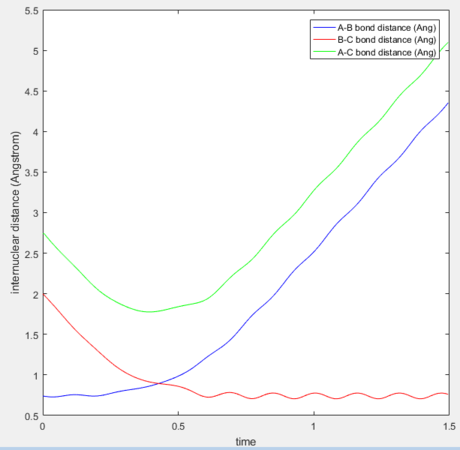
This reaction trajectory leads to the successful formation of the product. It follows the valley of the valley of the potential energy surface and displays very little vibrational energy.
p1= -1.5, p= -2.0 Reaction Unsuccessful
The H and H2 do not have sufficient translational energy to react. The atoms come together but collapse back down their initial state.
p1= -1.5, p= -2.5 Reaction Successful
In a similar case for the first conditions, the reaction takes places but this is not surprising due to the subtle change in the initial kinetic energy.
p1= -2.5, p= -5.0 Reaction Unsuccessful
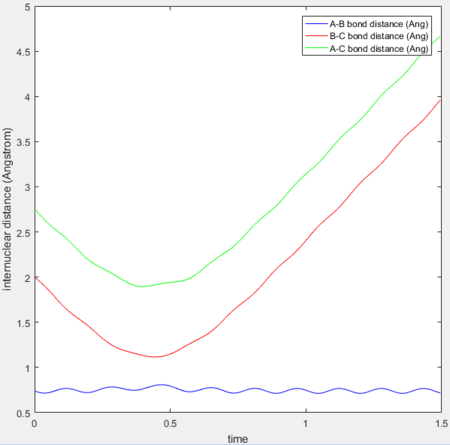
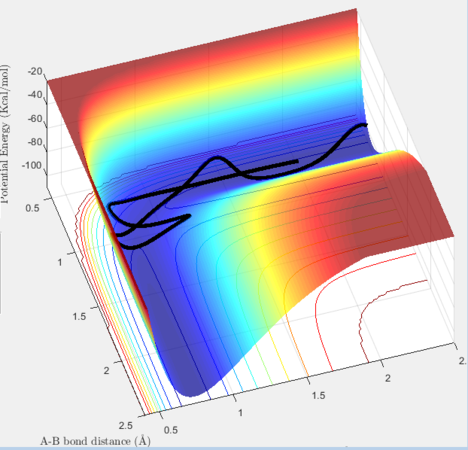
These initial distance and momentum conditions lead to an interesting reaction in which the product is formed in transition state but the reactants separate and return to their side of the potential valley. The barrier recrossing is due to the extension of the bond as it breaks after formation.
p1= -2.5, p= -5.2 Reaction Successful
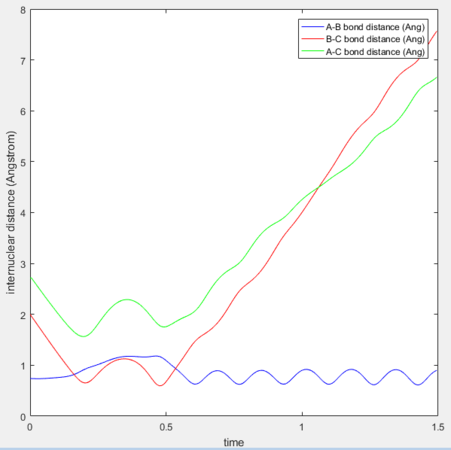
The hydrogen exchange occurs but the product has very high vibrational energy. This could be a consequence of the system possessing very high energy. It crosses and recrosses until it has the correct ratio of energies.
Main Assumptions in Transition State Theory
The governing equation of transition state theory is Eyring's equation
The main assumptions in transition state theory are
- All steps preceding the formation of the activated complex are not considered
- Atoms are considered as hard spheres
- All translational energy can be ascribed to kinetic energy and momentum
- Quantum mechanical effects including tunnelling are ignored
- If the system is at equilibrium the transition state is at equilibrium and is unaffected by removing product
- One reaction pathway
- Limited recrossing of the barrier
- Obeys Boltzmann distribution
The combined effect of these assumptions is that the observed rate is higher than that predicted by theory [1].
Potential Energy Surface and Reaction Dynamics of an F - H - H system
Inspection of the F + H2 → HF + H Potential Energy Surface
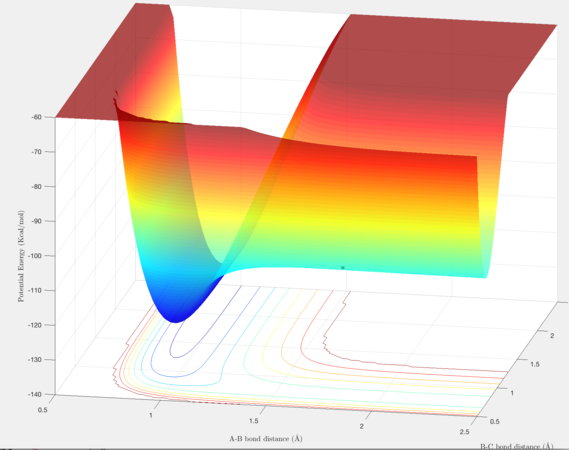
The F + H2 → HF reaction is exothermic because the product is more energetically stable than the reactants. Conversely the reverse reaction is endothermic because the reactants are more energetically stable than the products. Intuitively this is expected as is the H-F bond is significantly stronger than H-H due to the strong polarisation of the bond.
The transition state was located by visual inspection of a contour plot for the saddle point. It is an early transition state in the exothermic direction (similar to the reactants) and late in the endothermic direction (similar to the products). The activation energy for F + H2 → HF + H is very small and so applying Hammond's postulate, in which the transition state resembles reactant or product it closer to in energy allows it determination. The transition state was found at (1.814, 0.745) .
F + H2 → HF + H Activation Energy= 0.6 kcal-1
H + HF → H2 + F Activation Energy= 30.4 kcal-1
Experimental Techniques for Analysing the F + H2 system
In the reaction trajectory for F + H2 → HF + H , after reaching the transition state the energy is released into the vibrational mode. The HF molecule displays significant vibrational oscillations as evidenced by the oscillating internuclear momenta against time.
Hence using vibrationally resolved spectroscopy, the reaction dynamics can be investigated. Tizniti et al simulated the conditions of deep space and analysed the reaction using pulsed laser photolysis–pulsed laser-induced fluorescence [2] . This would allow for probing of vibrational modes, which could be rationalised using the Frank Condon principle. The FH2- ion is readily characterised and as it is close in energy and semblance to the transition state. Qui et al were able to analyse the reaction from a full quantum mechanical perspective using an advanced crossed molecular beam scattering technique in conjunction with the time of flight measurements of Rydberg tagged hydrogen radicals [3].
Energy Distribution between Vibrational and Translational Modes
F + H2 → HF + H
For the collision of a fluorine radical into a hydrogen molecule, translational energy is considerably more important than vibrational energy. The early transition state means that momentum is more effective when supplied along the bond axis. It is an early barrier exothermic reaction. As the energy released by H-H repulsion is supplied before the H-F bond reaches its equilibrium position, it causes the bond to vary in length - vibrational energy [4].
H + HF → H2 + F
In this direction, vibrarional energy is more important as the momentum supplied to H-F elongates and weakensthe strong bond between hydrogen and fluorine. It is a late barrier endothermic reaction. Consequently, the energy supplied from the formation of the H-H bond is in the form of translational energy.
- ↑ K. J. Laidler and M. C. King, J. Phys. Chem., 1983, 87, 2657–2664.
- ↑ M. Tizniti, S. D. Le Picard, F. Lique, C. Berteloite, A. Canosa, M. H. Alexander and I. R. Sims, Nat Chem, 2014, 6, 141–145.
- ↑ M. Qiu, Z. Ren, L. Che, D. Dai, S. A. Harich, X. Wang, X. Yang, C. Xu, D. Xie, M. Gustafsson, R. T. Skodje, Z. Sun and D. H. Zhang, Science (80-. )., 2006, 311, 1440 LP-1443.
- ↑ J. C. Polanyi and J. L. Schreiber, Faraday Discuss. Chem. Soc., 1977, 62, 267–290.