MRD:01053372
Molecular Reaction Dynamics: Applications to Triatomic systems
EXERCISE 1: H + H2 system
Potential Energy Surfaces
Q1: What value do the different components of the gradient of the potential energy surface have at a minimum and at a transition structure? Briefly explain how minima and transition structures can be distinguished using the curvature of the potential energy surface.
The Potential Energy surface of a system shows how the potential varies with distance in a 3D plot. Two points of interest are minima and transition states.
(Which distance do you mean exactly? You need to explain that this is a triatomic system and that we're looking at the interatomic distances. Fjs113 (talk) 16:21, 14 May 2018 (BST))
At a minimum and at a transition structure the gradient has a 0 value. For a transition state there is a saddle point, this means in one direction there is a minimum and so 0 gradient, and in the orthogonal direction there is a maximum and so 0 gradient. They can be identified on a potential energy surface by finding the "flat" parts of the surface, for example by starting a trajectory near the transition state and seeing which way the reaction goes, to reactants or products (The transition state will be in the opposite direction).
(This is all correct. It would've been nice if you used mathematical terms such as first and second order partial derivatives to characterise the minimum and the saddle point. Fjs113 (talk) 16:21, 14 May 2018 (BST))
Estimating the Transition State
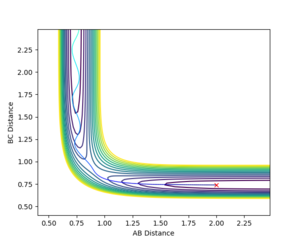
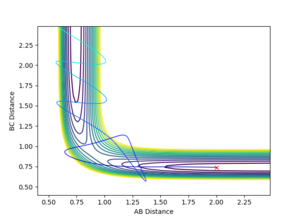
Q2: Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” plot for a relevant trajectory.
To find the TS first a surface plot of the system was used to identify where the likely positioning would be. Since the system is symmetric it was assumed the TS would lie along the XY diagonal, therefore r(AB) and r(BC) would be equal for the TS. Following this an initial trajectory was set up where p(AB) and p(BC) were 0, and the position along the XY diagonal was varied. Eventually when the 'Internuclear Distance' vs time graph showed no vibration, it was clear the TS had been reached (the system did not move, so no forces were acting on it and therefore the gradient on the PES was 0)
(Perfect explanation! Fjs113 (talk) 16:21, 14 May 2018 (BST))
r(ts)= 0.908 to 3 s.f.
It can be seen from the Internuclear Distance vs Time graph that at 0.908 a.u for AB and AC there is no oscillation, which means we are on a point of 0 gradient on the potential energy surface, which is the TS saddle point.
MEP
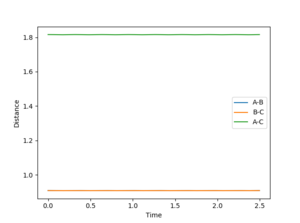
Q3:Comment on how the mep and the trajectory you just calculated differ.
An MEP was carried out with initial conditions of r1 = r(ts)+0.01, r2 = r(ts)
The MEP results is the minimum energy path, this is achieved by resetting the velocity to 0 at each time step. Therefore with the MEP no oscillations are observed in the BC bond distance. On the other hand the reaction path from the same starting position has an oscillating BC bond, as the initial inertia in BC direction sets up a vibration.
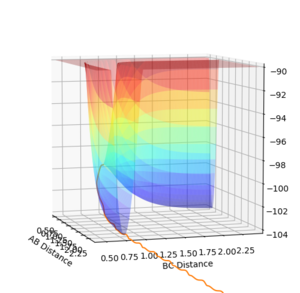
An inversion of momentum procedure was then carried out, by taking the las Geometry from the MEP trajectory and reversing the momentum. This resulted in forming a system which ended in the TS.
Last Geometry:
Final r(AB): 9.004725826979717
Final r(BC): 0.7400803088831149
Final p(AB): -2.4806505081787176
Final p(BC): -0.9082751884031437
(Good! Fjs113 (talk) 16:21, 14 May 2018 (BST))
Reactive Trajectories
Q4:Complete the table by adding a column with the total energy, and another column reporting if the trajectory is reactive or unreactive. For each set of initial conditions, provide a plot of the trajectory and a small description for what happens along the trajectory.
| Set | p1 | p2 | total energy | reactivity | ||
|---|---|---|---|---|---|---|
| i | -1.25 | -2.5 | -99.018 | Yes |  |
Atom A approaches the B-C molecule, they collide, and have enough energy to move over the transition state. An A-B bond is formed which oscillates due to the energy from the collsison. The B-C bond is broken so the C molecule atom away from A-B molecule. |
| ii | -1.5 | -2.0 | -100.456 | No |  |
Atom A approaches an oscillating B-C molecule, they collide, but do not have enough energy to pass over the transition state. This results in the B-C bond remaning and the C atom and B-C molecule 'bouncing' away from each other |
| iii | -1.5 | -2.5 | -98.956 | Yes |  |
Atom A approaches an oscillating B-C molecule, they collide, and have enough energy to move over the transition state. An A-B bond is formed which oscillates due to the energy from the collsison. The B-C bond is broken so the C molecule atom away from A-B molecule. |
| iv | -2.5 | -5.0 | -84.956 | No |  |
Atom A approache the B-C molecule, they collide and form an A-B molecule and a C atom. However the A-B molecule has so much excess energy from the collision that it's oscillations lead to a reforming of the B-C bond, which moves away from the A atom. This is known as barrier crossing. |
| v | -2.5 | -5.2 | -83.416 | Yes |  |
Atom A approaches the B-C molecule, they collide and form an A-B molecule and a C atom. The A-B molecule has so much excess energy it reforms the B-C molecule. The B-C molecule in turn vibrates with a great enough amplitude to reform the A-B molecule and C atom, which move away from eachother. This is double barrier crossing. |
Transition State Theory
Q5:State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?
Transition state theory describes how a chemical reaction will occur based on the “transition state” that this reaction has and it is based upon collision theory.
There are three main assumptions in Transition State Theory: 1) In a multi step mechanism we assume each intermediate exist for long enough to achieve a Boltzmann distribution of energies before it continues. This may not be true, and the momentum of the reaction trajectory can lead to selectivity. 2) We assume that the atomic nuclei behave according to classical mechanics. However quantum mechanical tunneling can lead to a reaction even if the energy barrier is higher than the reactants energy. This affect can be important for low activation energy reactions. 3) We assume that the system passes over the lowest energy saddle point. For high temperatures with complex vibrations occurring, this may not be true. [1]
In General TST will over estimate the rate. This is because we are assuming in (1) that each intermediate exists in Boltzmann distribution quantities, when this is not really true. So there will be less intermediates present in reality and therefore a lower rate. On top of the for more complex systems, we have not considered the angle of approach, If there is a required angle of approach some trajectories, although reactive from a kinetic perspective, will not actually lead to a reaction. Finally by assuming in (2) that the systems behave classically, we have ignored the effects of Quantum tunneling.
(Well researched answer. However, you did not mention that classical TST does not consider barrier recrossing, an effect that you can see happening in the last two simulations in the previous question. This is mainly the reason why TST will over-estimate the reaction rate in classical conditions. Fjs113 (talk) 16:21, 14 May 2018 (BST))
EXERCISE 2: F - H - H system
Reaction Enthalpy
Q1: Classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?
The Bond energies for HF and HH are given in the following table:[2]
| Bond | Energy |
|---|---|
| H-F | 565 kJ/mol |
| H-H | 432 kJ/mol |
F + HH is Exothermic, as can be seen from the decrease in energy of the Reactants to the products.
This makes sense because we form a stronger F-H bond and break a weaker H-H bond, releasing energy.
H + HF is endothermic, as can be seen from the increase in energy from the Reactants to the products.
This makes sense because form a weaker H-H bond and break a stronger H-F bond.
Estimating the Transition State
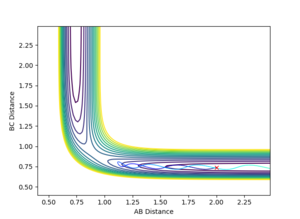
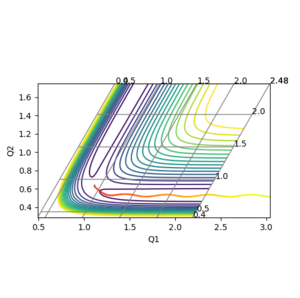
Q2: Locate the approximate position of the transition state.
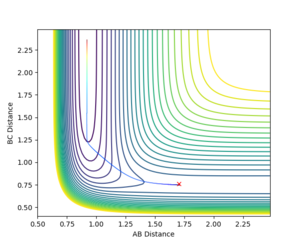
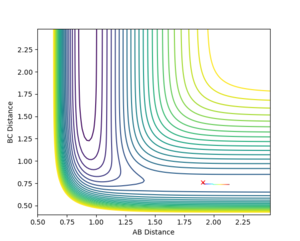
The transition state for the FHH system was not as easy to locate as the symmetric HHH system. Hammond's Postulate was used to make a guess at the position, and using the Contour Plot the initial starting position was moved opposite to the movement of the reactants, until no movement was seen.
r(ts) AB 1.806 a.u, BC 0.759 a.u
Activation Energy
Q3: Report the activation energy for both reactions
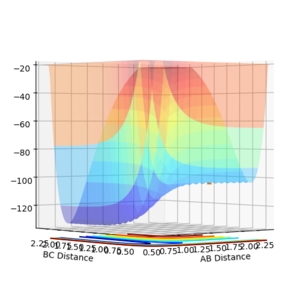
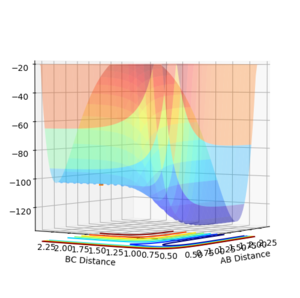
The Activation energy is the difference between the TS energy and the energy of the reactants, i.e the energy required to push the reactants over the TS. The energy of the TS was recorded as -103.676 from the r(ts). An MEP was then carried out with r(AB) = r(ts) ± 0.1 and the final geometry of those reactions was used to find the energy of the reactants of H+HF and F+HH.
Activation Energy = T.S Energy - Reactant Energy
H+HF: -103.676 + 133.941 = 30.265
F+HH: -103.676 + 103.957 = 0.281
Reactive Trajectories
Q3: In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. How could this be confirmed experimentally?
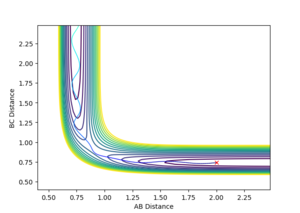
The Initial Conditions which lead to a reactive trajectory where rF-H = 2.0, rH-H = 0.73, pF-H = -2.0, pH-H = -1.3
(Please explain/illustrate how you reached these initial conditions, even if it was just an educated guess! Fjs113 (talk) 16:21, 14 May 2018 (BST))
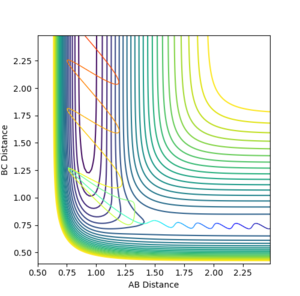
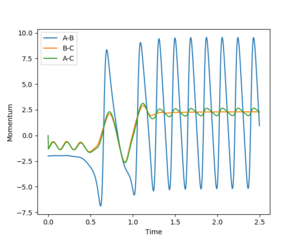
The Mechanism for this process can be deduced from the Momentum vs Time graph. It can be seen that the momentum of the initial vibration of the H2 molecule and the momentum of the H2 and F species moving towards each other is very small compared to the final vibration of the F-H molecule formed. From the surface plots of this reaction we know it is exothermic, and due to the law of conservation of energy, it is logical to say that the released energy was converted to vibrational energy in the F-H molecule.
This could be confirmed through IR Spectroscopy. Where the F-H molecule which would be in a vibrationaly excited state would display overtone bands.
Polanyi's empirical rules
Q4:Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.
John Polanyi in 1972 proposed what is known as Polayni's rules, which determine whether vibrational or rotational energy is more likely to lead to a reactive trajectory. The rules apply to atom to di-atom collisions and states that vibrational energy is more efficient in promoting a late transition state reaction, whereas translational energy is more likely in promoting a early transition state reaction.[3]
Hammond's postulate states that a transition state will resemble the species closest in energy to it. Therefore an exothermic reaction has an early transition state resembling the high energy reactants, and an endothermic reaction has a late TS resembling the high energy products.
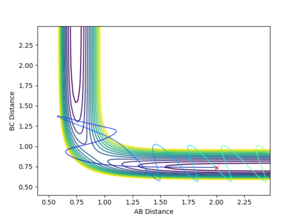
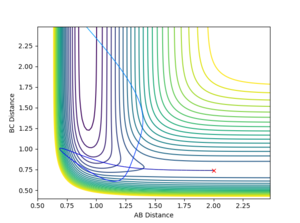
The F + HH reaction, is Exothermic (early TS) and therefore according to Polayni's rules a reactive trajectory is favoured by translational energy.
Initial Conditions r(FH)=2 r(HH)=0.74
It was observed that at lower values of p(HH) a reaction was more likely, and at higher values of p(HH) it was less likely.
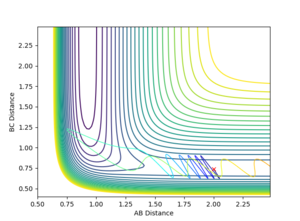
The H + HF reaction is endothermic (Late TS) and therefore according to Polayni's rules a reactive trajectory is favoured by vibrational energy.
Inital Conditions r(HH) = 2, r(HF) = 0.9
It was observed that at higher values of p(HF), the reaction was likely to be reactive.
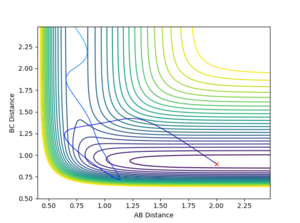
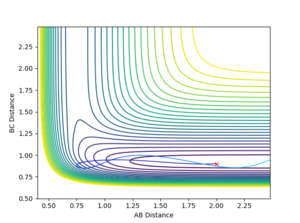
(Some great examples here! Fjs113 (talk) 16:21, 14 May 2018 (BST))
- ↑ https://en.wikipedia.org/wiki/Transition_state_theory.
- ↑ http://www.wiredchemist.com/chemistry/data/bond_energies_lengths.html
- ↑ Theoretical Study of the Validity of the Polanyi Rules for the Late-Barrier Cl + CHD3 Reaction Zhaojun Zhang, Yong Zhou, Dong H. Zhang, Gábor Czakó, and Joel M. Bowman The Journal of Physical Chemistry Letters 2012 3 (23), 3416-3419 DOI: 10.1021/jz301649w