MRD:01023138jw7815

Exercise 1: H + H₂ system

What value does the total gradient of the potential energy surface have at a minimum and at a transition structure? Briefly explain how minima and transition structures can be distinguished using the curvature of the potential energy surface.

In a Potential Energy Surface (PES), the first derivative refers to the gradient of a point on the surface; while the second derivative refers to the rate of change of gradient of a point on the surface, also known as the curvature. A positive curvature implies that the gradient changes from negative to zero to positive (minimum point), a negative curvature implies that the gradient changes from positive to zero to negative (maximum point), and zero curvature implies that the gradient changes from negative to zero to negative or positive to zero to positive (saddle point).

The gradient of the potential energy surface at a minimum and at a transitions structure are both zero.

The minima and transition structures can be differentiated by their curvatures because the minima has a positive curvature (minimum point), while the transition structure has zero curvature (saddle point).

Not entirely sure what you mean here. At a TS, one of the second partial derivates is >0 and all the others are <0 Je714 (talk) 17:15, 31 May 2017 (BST)

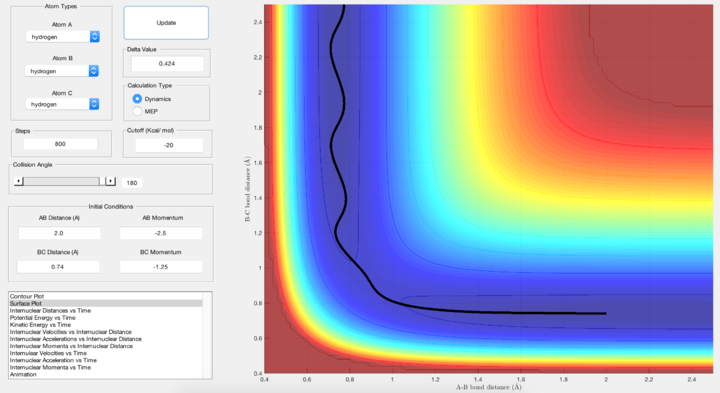
Report your best estimate of the transition state position (r_ts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” screenshot for a relevant trajectory.

From the "Internuclear distance vs Time" plot, the best estimate was obtained when r_ts = 0.9075 Å. With reference to the above Figure, the value was obtained by varying the values of r₁ = r₂ until the internuclear distance vs time behaviour switches from "oscillating" to just a steady horizontal line. A steady horizontal line means that the internuclear distances are constant with time, and is expected because a transition state will remain in its position indefinitely when the momentum p₁ and p₂ is zero. Why? Je714 (talk) 17:16, 31 May 2017 (BST)

Comment on how the mep and the dynamic trajectory calculated differ.

Using r₁ = r_ts + 0.1 and r₂ = r_ts;

In mep, the trajectory follows the valley floor as a non-oscillating straight line because the velocity is reset to zero in each time step, and the trajectory will only move in the direction of the steepest slope (towards the product).

In dynamic, the trajectory follows the valley as an oscilllating line because it takes into accout the initial velocity, which will influence its subsequent motion in the next time step.

Good Je714 (talk) 17:16, 31 May 2017 (BST)

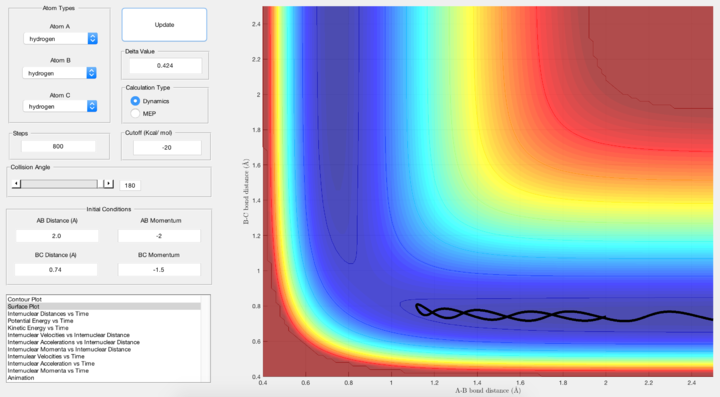
Complete the table by adding a column reporting if the trajectory is reactive or unreactive. For each set of initial conditions, provide a screenshot of the trajectory and a small description for what happens along the trajectory.

In the following analyses, it is important to point out that the momentum we are adjusting is directly proportional to the kinetic energy required to overcome the activation barrier ( KE = p²/2m).

Reaction	p₁	p₂	Reactive/Unreactive	Description
1	-1.25	-2.5	Reactive	As A approaches B-C, the AB momentum is high enough such that the kinetic energy is sufficient to overcome the activation barrier, thus the trajectory will pass through the transition state to form A-B, with a bond distance of around 0.70. There is greater oscillation once the transition state is passed, implying that the product A-B has more vibrational energy than the reactants.
2	-1.5	-2.0	Unreactive	As A approaches B-C, the AB momentum is not high enough and there is insufficient kinetic energy to overcome the activation barrier for the trajectory to pass through the transition state to form A-B. The trajectory thus shows an initial decrease in A-B bond length until around 1.1 Å, but increases back to its initial value (to reactants) and is unreactive.
3	-1.5	-2.5	Reactive	As A approaches B-C, the AB momentum is high enough such that kinetic energy is sufficient to overcome the activation barrier, thus the trajectory will pass through the transition state to form A-B, with a bond distance of around 0.70. Unlike Reaction 1, the product A-B has only slightly more vibrational energy than the reactants as indicated by the greater degree of oscillation once it passes through the transition barrier.
4	-2.5	-5.0	Unreactive	As A approaches B-C, the AB momentum is high enough such that kinetic energy is sufficient to overcome the activation barrier, however, while the trajectory initially crosses the transition barrier towards the product, it eventually recrosses back towards to reactants, and the reactant is reformed with a much higher vibration energy.
5	-2.5	-5.2	Reactive	As A approaches B-C, the AB momentum is higher enough such that the kinetic energy is sufficient to overcome the activation barrier. In this case, the trajectory passes through the transition barrier to the products, but recrosses to the reactants and then back to the product A-B, which has a bond length of around 0.70 Å and possess a much greater vibrational energy than the reactants.

State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?

The transition state theory is used to qualitatively understand how chemical reactions take place. The following are key assumptions made in this theory:

The theory assumes that the atomic nuclei follow classical mechanics, where sufficient kinetic energy must be present to overcome the activation barrier. This is not true because in quantum mechanics, atoms with insufficient energy can still tunnel through the activation barrier without actually "overcoming" it.
The theory assumes that barrier recrossing does not occur, as seen in reaction 4 and 5. This means that if a trajectory passes through the activation barrier, it must lead to products. However, from reaction 4, we see that this is not necessarily true - recrossing occured to reform the reactants. This highlights that even if a molecule possesses sufficient kinetic energy to overcome the activation barrier, there are other factors that must be considered for a successful reaction.
The theory assumes that the intermediates have a sufficiently long lifetime to reach a Boltzmann distribution of energies before forming the products. In reality, intermediates are not long-lived and exist on a timescale of around 10^-13 seconds, which is insufficient for the Boltzmann distribution to be reached. This is a statistical mechanics consideration that is not really applicable in our simulations. We're just looking at a triatomic collision in isolation -- no ensemble of particles are considered here. Je714 (talk) 17:18, 31 May 2017 (BST)

The theory assumes that the reaction trajectory passes through the transition state (saddle point on the PES) before reaching the product. This is not necessarily the case, and we see in reaction 5 that s possible for trajectories to result in product without having passes through the saddle point.
The theory only assumes 3 possible states in the reaction - the reactants, transition complex, and the products, anything else is not considered.

Apart from these assumptions, it is important to highlight that the transition state theory may not apply at elevated temperatures because molecules begin to populate higher vibrational modes and result in complex motion which may lead to transition states far away from the lowest energy saddle point.

So, does TST under or over estimate reaction rates? You forgot to discuss that. Je714 (talk) 17:18, 31 May 2017 (BST)

Exercise 2: F + H₂ system

Classify the F + H₂ and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?

Bond	Bond Strength^[1]/kJ mol^-1
H-F	565
H-H	432

For F + H₂, the reaction is exothermic as the product energy is lower than the reactant energy as seen in the potential energy surface. This is in agreement with the prediction based on bond strengths, as the H-F bond being formed is stronger than the H-H bond being broken, resulting in a net lowering of energy.

For H + HF, the reaction is endothermic as the product energy is higher than the reactant energy as seen in the potential energy surface. Once again, this is to be expected as the H-H bond being formed is weaker than the H-F bond being broken, resulting in a net raising of energy.

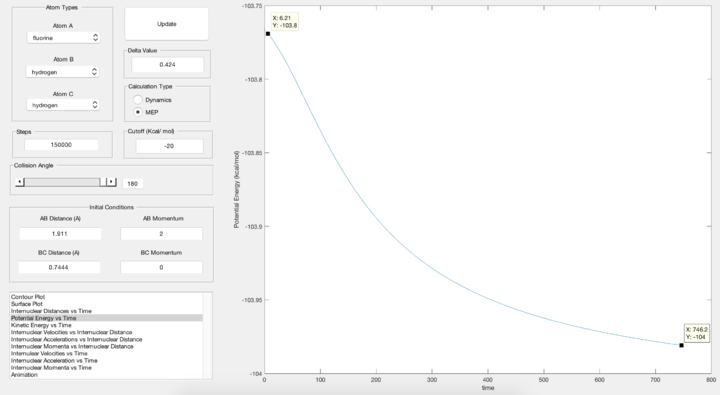
Locate the approximate position of the transition state.

From the "Internuclear distance vs Time" plot, a constant internuclear distance is obtained (as shown above) when r_HH = 0.744 Å and r_HF = 1.811 Å.

Report the activation energy for both reactions.

F + H₂ -> HF + H

For this illustration, the reactants are F + H₂ and the products are HF + H.

Direction of Reaction	Potential Energy vs Time	Energy/kJ mol^-1
Transition State -> HF + H		Transition State = -103.8 Products (HF + H) = -133.9
Transition State -> F + H₂		Transition State = -103.8 Reactants (F + H₂) = -104.0

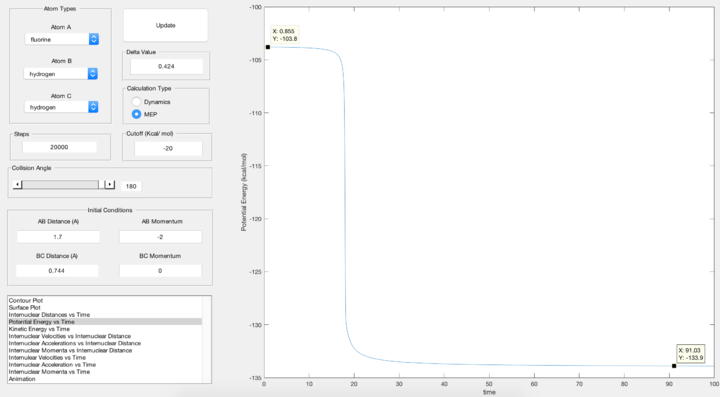
Forward Reaction: F + H₂-> HF + H

Activation Energy = -103.8 - (-133.9) = 30.1 kcal/mol

Backward Reaction: H + HF -> F + H₂

Activation Energy = -103.8 - (-104.0) = 0.2 kcal/mol

In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. How could this be confirmed experimentally?

In the forward exothermic reaction F + H₂ -> H + HF, the reactants posses more potential energy than the products. Because of conservation of energy, during the course of the reaction, the potential energy and is converted to kinetic energy. This reaction energy released in the form of kinetic energy can be converted to vibrational energy and translational energy, and can be detected through infrared chemiluminscence or through temperature measurements.

Infrared Chemiluminescence

From the above trajectory, it can be seen that the product H-F has a greater vibrational energy than the reactant H-H represented by the greater degree of oscillations. The infrared emission of the vibrationally excited product can be measured using methods such as infrared chemiluminescence ^[2].

Temperature Measurements

If reaction energy is released as heat (i.e. thermal energy), this can also be measured experimentally by monitoring the increase in temperature as the reaction progresses.

Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.

For an efficient reaction, the reactants must not only have sufficient energy, but should have the right distribution of kinetic energy between the vibrational and translational components. Polanyi's empircal rules states for reactions with late transition states, vibrational energy is more effective than translational energy for an efficient reaction, while for reactions with early transition states, translational energy is more effective than vibrational energy for an efficient reaction.

According to Hammond's postulate, endothermic reactions have a late transition state, while exothermic reactions have an early transition state. Thus, his rules can be reframed to mean endothermic reactions prefer vibrational energy, while exothermic reactions prefer translational energy.

Direction of Reaction	Thermodynamics of Reaction	High Vibrational Energy, Low Translational Energy	Low Vibrational Energy, High Translational Energy	Analysis using Polanyi's Rule
Forward (F + H₂ -> HF + H)	Exothermic	p_HF = -0.1 (Low translational momentum) p_HH = 0.8 (High vibrational momentum)	p_HF = -0.8 (High translational momentum) p_HH = 0.1 (Low vibrational momentum)	In both cases, the total energy is the same. In the first case with low translational energy, the trajectory is unreactive. However, with high translational energy, the trajectory becomes reactive. This is in line with Polanyi's rule, since translational energy is more important for an effective reaction when the process is exothermic.
Backaward (H + HF -> F + H₂)	Endothermic	p_HF = 6.5 (High vibrational momentum) p_HH = -1.5 (Low translational momentum)	p_HF = 1.5 (Low vibrational momentum) p_HH = -6.5 (High translational momentum)	In both cases, the total energy is the same. In the first case with high vibrational energy, the trajectory is reactive. As soon as the vibrational energy is lowered in the second case, the trajectory becomes unreactive. This is in line with Polanyi's rule, since vibrational energy is more important for an effective reaction when the process is endothermic.

References

↑ Y. R. Luo, Comprehensive handbook of chemical bond energies. CRC press., 2007.
↑ J. C. Polanyi, J. Quant. Spectrosc. Radiat. Transf., 1963, 3, 471–496.

[1] Y. R. Luo, Comprehensive handbook of chemical bond energies. CRC press., 2007.

[2] J. C. Polanyi, J. Quant. Spectrosc. Radiat. Transf., 1963, 3, 471–496.

[1]

[2]

Exercise 1: H + H2 system