MRD:00941400
EXERCISE 1: H + H system
Dynamics from the transition state region
What value does the total gradient of the potential energy surface have at a minimum and at a transition structure? Briefly explain how minima and transition structures can be distinguished using the curvature of the potential energy surface.
The gradient at a minimum and transition structure both equal zero. Transition structure can be distinguished as a saddle point in the potential energy surface. this is when the gradient of the orthogonal components are zero but are not local extrema. minima can be distinguished as point point where again the gradient of the orthogonal components are zero and also are local minima.
Trajectories from r1 = r2: locating the transition state
Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a Internuclear Distances vs Time screenshot for a relevant trajectory.
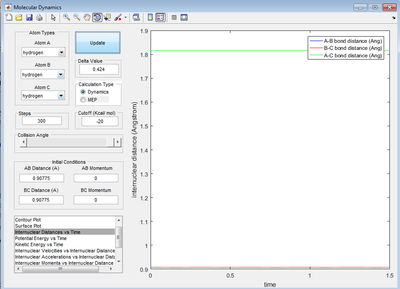
0.90775 Å. In the animation section, when you change the distance from this by 0.00001 Å or 0.000001 Å the distance varies between 0.9077 and 0.9078 Å. In the image below it shows internuclear distance vs time plot in which the BC and AC distance have horizontal lines. Changing the distance AB and BC to 1 Å shows a sinusoidal curve instead of horizontal lines.
Trajectories from r1 = rts+δ, r2 = rts
Comment on how the mep and the trajectory you just calculated differ.
in the mep calculation with 1500 steps the internuclear distance vs time for AB bond length falls from transition state length to about 0.74 Å and BC length increases whereas in the dynamics calculation with 300 steps the AB bond length has oscillates between 0.72 and 0.76 Å after falling from the transition state length and BC bond length just increases.
What would change if we used the initial conditions r1 = rts and r2 = rts+0.01 instead?
the opposite occurs, BC length in 0.74 Å and AB length increases. from transition state it "falls" to the reactant side.
What do you observe?
The only difference that occurs in this run compared to the initial run is that there is no oscillation of the distance between BC as A approaches, the momentum between BC and momentum of A cancel out.
Reactive and unreactive trajectories
Complete the table by adding a column reporting if the trajectory is reactive or unreactive. For each set of initial conditions, provide a screenshot of the trajectory and a small description for what happens along the trajectory.
| p1 | p2 | reactive |
|---|---|---|
| -1.25 | -2.5 | yes |
| -1.5 | -2.0 | no |
| -1.5 | -2.5 | yes |
| -2.5 | -5.0 | no |
| -2.5 | -5.2 | yes |
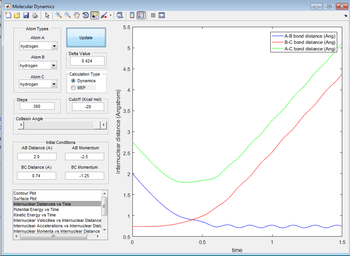
The reaction proceeds in the normal fashion.
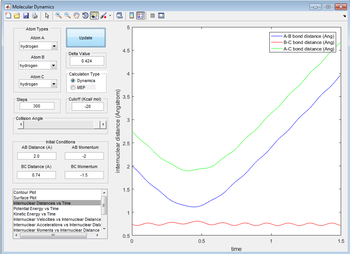
The reaction does not proceed. Atom A does not have enough momentum to get close to the transition state separation of 0.90775 Å, instead getting to 1.117 Å and going back.
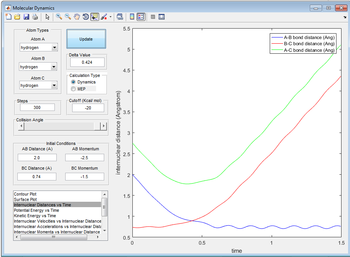
The reaction just about proceeds.If the momentum between AB was -2.4 the reaction wouldn't proceed.
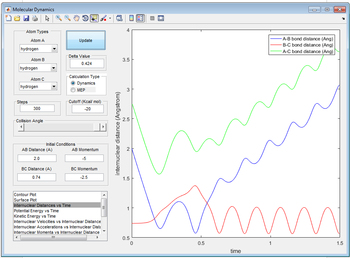
The reaction does proceed but then it reverts back to the reactants. This is due to the momentum between BC being high enough to push A away.
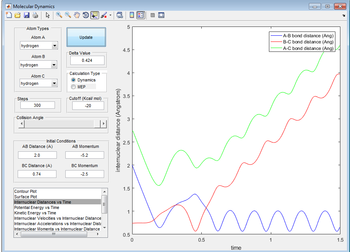
The reaction proceeds in an abnormal fashion. what occured above started happen in this as well but the momentum was high enough between AB to eventually push C away.
State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?
Assumption: nuclei behave in a classical mechanics way.However from quantum mechanics we know that tunnelling between barriers occur even if there's not enough energy. This means the reaction rates calculated by this theory will be different to experimentally calculated ones probably the theoretical value produces rate values that are smaller than experimentally calculated values.
(What about an assumption that conflicts with what you have shown above? Tam10 (talk) 16:43, 22 May 2017 (BST))
EXERCISE 2: F - H - H system
PES inspection
Classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?
F + H2 is an exothermic reaction and H + HF is and endothermic reaction. HF bond is much stronger than H2 bond and hence needs more energy to break HF bond and relatively less energy is released when HH bond forms in the reaction.
Locate the approximate position of the transition state.
Using 2000 steps the position of the transition state was calculated. HF = 1.80718 Å. HH = 0.7638426065 Å. These values are only approximate, knowing exactly the value would require a better computation on a better computer probably.
(What calculation did you perform? Unfortunately, despite your high level precision, you're a bit off the TS. Tam10 (talk) 16:43, 22 May 2017 (BST))
Report the activation energy for both reactions.
The activation energy of F + H2 was calculated as 0.837 kJ/mol and of H + HF was calculated as 125.6 kJ/mol. These were calculated using mep function in the potential energy vs time to hundreds of thousands of steps with zero potential and distance set to close to transition point, changing slightly from transition point to get the correct product versus the other.
Reaction dynamics
In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. How could this be confirmed experimentally?
Some of the energy is released as kinetic energy of the leaving H atom. The periodic momentum between HF is much higher than that of HH at the start meaning higher kinetic energy for HF. energy is released after the transition state as the HF starts to vibrate and H moves away.
Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.
For high translational energy of incoming atom vs low vibrational energy of the molecule, the reactant converts to products in one go within 2 min of start. For the opposite, the reaction does proceed but often include some reverting back to reactant a few times before settling in the product form.
Transition point can be thought of as [H----H---------F]. For F + H2, when translational energy is low and high vibrational energy the reaction takes longer to proceed vs the opposite scenario. this can be understood from the transition point, F is much farther form H so needs energy to get close to a bonded position and not having the translational energy makes it longer for reaction to proceed. For H + HF, when vibrational energy is high and translational is low the HF bond elongates more getting to the transition point quicker and hence the reaction proceeds slightly faster than for the opposite.
(I think you mean it's an early TS Tam10 (talk) 16:43, 22 May 2017 (BST))