MOSAsghar
EX3 Section
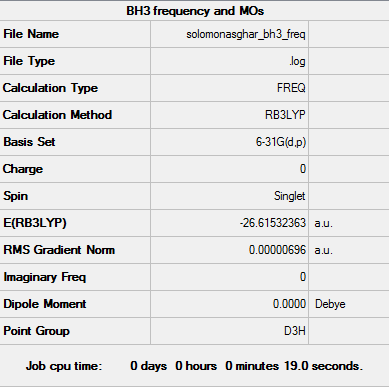
BH3
B3LYP/6-31G(d,p)
Item Value Threshold Converged? Maximum Force 0.000014 0.000450 YES RMS Force 0.000007 0.000300 YES Maximum Displacement 0.000055 0.001800 YES RMS Displacement 0.000027 0.001200 YES
Frequency file: SOLOMON ASGHAR BH3 FREQ.LOG
Low frequencies --- -7.9073 -1.6385 -0.0054 0.6256 6.5697 6.7709 Low frequencies --- 1162.9662 1213.1623 1213.1650
Optimized BH3 Molecule |
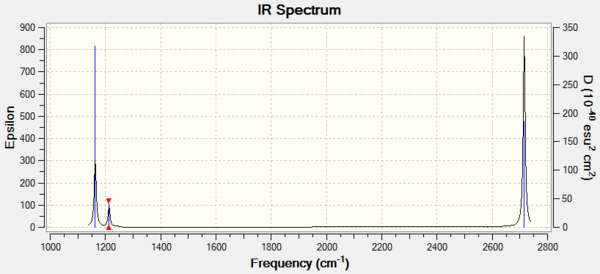
Vibrational spectrum for BH3
| wavenumber (cm-1 | Intensity (arbitrary units) | symmetry | IR active? | type |
| 1163 | 93 | A2 | Yes | out-of-plane bend |
| 1213 | 14 | E' | very slight | bend |
| 1213 | 14 | E' | Very Slight | bend |
| 2582 | 0 | A1' | No | symmetric stretch |
| 2716 | 126 | E' | Yes | asymmetric stretch |
| 2716 | 126 | E' | Yes | asymmetric stretch |
|
Some of the vibrations have the same wavenumber and intensity, these vibrations are degenerate and will give rise to a single peak in the spectrum. There are two sets of degenerate vibrations. One of the vibrations has an intensity of 0 - is not IR active. Because of these two factors, only 3 peaks will be observed.
Smf115 (talk) 08:01, 17 May 2018 (BST)Correct assignment of the modes and clear explaination which covers both the degenerate and IR inactive modes.
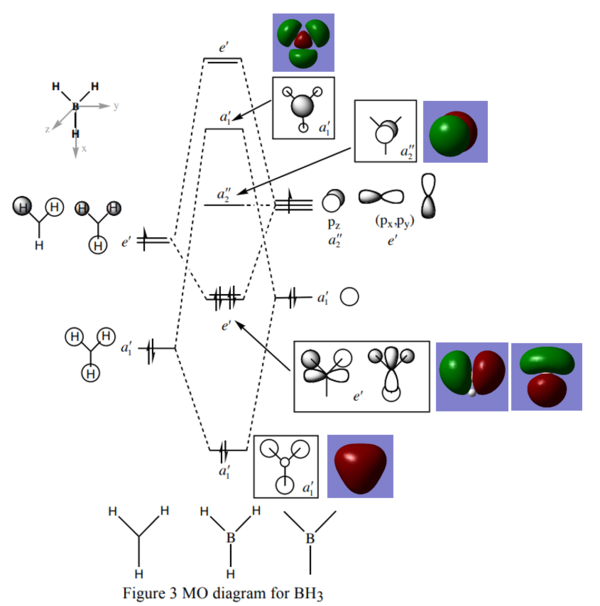
Qualitative MO diagram for BH3
|
Qualitative Molecular Orbital Diagram, taken from http://www.huntresearchgroup.org.uk/teaching/teaching_comp_lab_year2a/Tut_MO_diagram_BH3.pdf
The figure above shows a qualitative LCAO molecular orbital diagram for BH3, with MO surfaces computationally calculated with Gaussview also shown. Both methods predicted the same ordering of MO's, but naturally only qualitative methods give values for the energies. Note that the qualitative method shows accurately the relative size of the two orbitals in each combination, but represents the orbitals as discrete entities - they are not truly "combined". Only the computational method accurately shows the true overlap of the orbitals.
In spite of these limitations, for simple molecules, qualitative MO orbitals are able to elucidate bond orders, magnetic properties and reactivity.
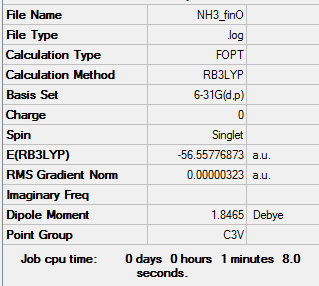
NH3
B3LYP/6-31G(d,p)
Item Value Threshold Converged? Maximum Force 0.000006 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000016 0.001800 YES RMS Displacement 0.000011 0.001200 YES
Frequency file: SOLOMON ASGHAR NH3 FREQ.LOG
Low frequencies --- -0.0138 -0.0032 0.0018 7.0783 8.0932 8.0937 Low frequencies --- 1089.3840 1693.9368 1693.9368
Optimized NH3 Molecule |
Vibrational spectrum for BH3
| wavenumber (cm-1 | Intensity (arbitrary units) | symmetry | IR active? | type |
| 1089 | 145 | A | Yes | out-of-plane bend |
| 1694 | 14 | E | very slight | bend |
| 1694 | 14 | E | very slight | bend |
| 3461 | 1 | A | very slight | symmetric stretch |
| 3590 | 1 | E | very slight | asymmetric stretch |
| 3590 | 1 | E | very slight | asymmetric stretch |
NH3BH3
B3LYP/6-31G(d,p)
Item Value Threshold Converged? Maximum Force 0.000116 0.000450 YES RMS Force 0.000060 0.000300 YES Maximum Displacement 0.000574 0.001800 YES RMS Displacement 0.000347 0.001200 YES
Frequency file: SOLOMON ASGHAR NH3BH3 FREQ.LOG
Low frequencies --- -12.0212 0.0005 0.0006 0.0010 9.2159 10.3218 Low frequencies --- 262.8497 631.2224 638.0448
Optimized NH3BH3 Molecule |
Energy Calculation
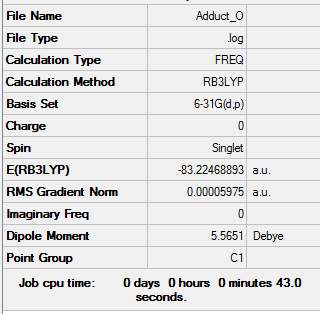
E(BH3)= -26.61532363 au E(NH3)= -56.55664124 au E(NH3BH3)= -83.22468893 au
ΔE= E(NH3BH3)-[E(NH3)+E(BH3)] ΔE= -83.22468893-[-56.55664124 - 26.61532363]
ΔE= -0.05272406 au ΔE= -138 kJ mol-1
The dative covalent bond is somewhat weak compared to other similar bonds (C-C 345 kJ mol-1), however it is still within the same order of magnitude.
Smf115 (talk) 21:47, 15 May 2018 (BST)Correct calculation procedure, however, the wrong energy for NH3 was used resulting in the wrong value. Good comparison to the C-C bond enthalpy but lacked a reference for it to be credited.
BBr3
B3YLP/GEN level
Item Value Threshold Converged? Maximum Force 0.000008 0.000450 YES RMS Force 0.000005 0.000300 YES Maximum Displacement 0.000036 0.001800 YES RMS Displacement 0.000023 0.001200 YES
Low frequencies --- -0.0137 -0.0064 -0.0046 2.4315 2.4315 4.8421 Low frequencies --- 155.9631 155.9651 267.7052
Frequency analysis log file: DOI:10042/202347
BBr3 |
Project Section
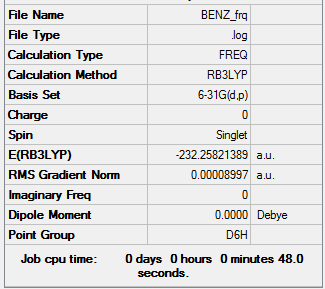
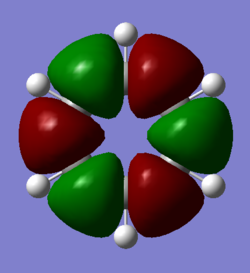
Benzene
Item Value Threshold Converged? Maximum Force 0.000202 0.000450 YES RMS Force 0.000090 0.000300 YES Maximum Displacement 0.000768 0.001800 YES RMS Displacement 0.000326 0.001200 YES
Low frequencies --- -2.5361 -2.5361 -0.0088 -0.0042 -0.0042 10.3972 Low frequencies --- 413.9725 413.9725 621.1357
Frequency analysis log file File:SOL-BENZ.LOG
Benzene |
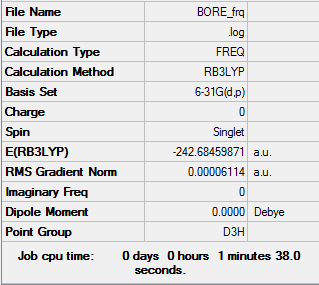
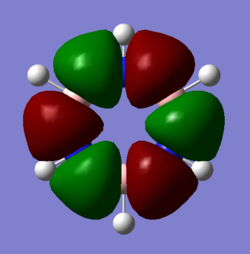
Borazine
Item Value Threshold Converged? Maximum Force 0.000193 0.000450 YES RMS Force 0.000061 0.000300 YES Maximum Displacement 0.000292 0.001800 YES RMS Displacement 0.000093 0.001200 YES
Low frequencies --- -3.0542 -0.0725 -0.0036 0.0178 1.3273 1.3345 Low frequencies --- 289.7139 289.7147 404.4142
Frequency analysis log file File:SA-BORE FRQ.LOG
Borazine |
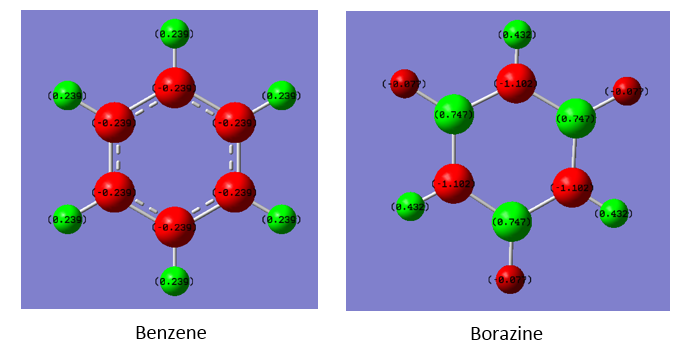
Comparison of Charges
| Atom | Charge (arbitrary units) |
|---|---|
| C | -0.239 |
| H | 0.239 |
| Atom | Charge (arbitrary units) |
|---|---|
| B | 0.747 |
| N | -1.102 |
| H (B-H) | -0.077 |
| H (N-H) | 0.432 |
Within benzene, charge is fairly negative and very equally distributed among all the carbon atoms present. This contrasts with borazine, in which church is much more unevenly distributed. The nitrogen's have a charge bellow the benzene carbons, and the boron's have a charge above them. This is exaclty the trend expected from the relative electronegativities of the species.
Smf115 (talk) 07:52, 17 May 2018 (BST)Clearly presented charges however, the colour range to highlight the charge distribution should have been the same across the molecules. The analysis is a bit brief and the idea of the electronegativity needs to be disscussed further with reference to the atoms and the charges.
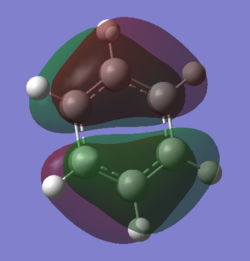
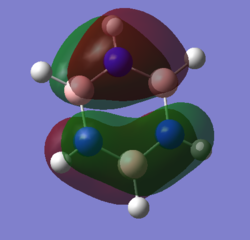
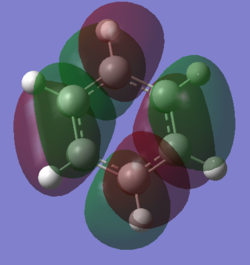
Comparison of Molecular Orbitals
Smf115 (talk) 08:03, 17 May 2018 (BST)Overall a well presented wiki report with thorough structure information given for both sections.Aromaticity
Initially, aromaticity was thought to occur exclusively in planar molecules with π-electron system. A simple set of rules, Hückel's rules, are often used to estimate weather a species will exhibit aromaticity. These rules state that for a molecule to be aromatic, it must:
1- Have 4n+2 electrons in a conjugated system of p-orbitals (where n is any integer)
2- Be planar
3- Be cyclic
4- Have a continuous ring of p AOs (atomic orbitals)
Although these rules often prove useful, it is known that they do not provide a complete view of aromaticity. Many molecules, such as metallobenzenes, 3D polyhedral boranes and fullerenes, do not satisfy these rules but still exhibit aromaticity. Ideas of quasi-aromaticity and quasi-rings complicate issues even beyond the common simplified view. Many contemporary scientists have even postulated that σ-electrons may be significant in bringing about aromaticity.
Smf115 (talk) 07:50, 17 May 2018 (BST)Nice mention of some contradictory examples. However, references should be seen and the asnwer is a little brief and the more complex ideas of aromaticity should be developed, such as sigma-aromaticity and mention of MOs.
Smf115 (talk) 08:00, 17 May 2018 (BST)Decent comparison of the MOs, good points are made and correct terminology used when comparing MO 14 and 15 and well compared due to shape and not by energy.
| Benzene MO | Borazine MO | Comparison |
|---|---|---|
 Benzene MO14 Energy= -0.46854 Hartrees |
 Borazine MO15 Energy= -0.43400 Hartrees |
Benzene MO 14 and borazine MO 15 are virtually identical in terms of shape and size. They are sigma bonding orbitals that arise from the overlap of Px or Py orbitals. All lobes are very slightly preferentially located on nitrogens over borons. There are many nodes in these orbitals, lowering stability. They occupy different levels in each molecule as the energy levels of the LCAO MOs produced varies between the species. |
 Benzene MO 21 Energy= -0.24691 Hartrees |
 Borazine MO21 Energy= -0.27591 Hartrees |
This level is the HUMO of both orbitals. Again, benzene's is much more symmetric than borazine's. In borazine, the nitrogen's contribute more to the orbital. Electron density extends to hydrogen atoms branching off of nitrogens, but not those attached to borons. |
 Benzene MO22 Energy= 0.00267 Hartrees |
 Borazine MO22 Energy= 0.02422 Hartrees |
This is the LUMO energy level of both molecules. For benzene, this orbital has very high symmetry - this is not the case with borazine. In borazine the boron atom contributes more strongly to the pi antibonding orbital than the nitrogen does, as it is higher in energy. Electron density does not reach any hydrogens branching off of nitrogens, but extends well to those attached to borons. |