MO:JGH116

Borane: BH₃

Key Data

The following calculation was performed using a B3LYP/6-31G(d,p) basis set:

Item Table

        Item               Value     Threshold  Converged?
 Maximum Force            0.000158     0.000450     YES
 RMS     Force            0.000079     0.000300     YES
 Maximum Displacement     0.000622     0.001800     YES
 RMS     Displacement     0.000311     0.001200     YES

The file for this calculation is here.

Frequencies

Low frequencies ---   -0.2456   -0.1129   -0.0054   44.0270   45.1846   45.1853
Low frequencies --- 1163.6049 1213.5924 1213.5951

Borane: BH3

Vibrations for BH₃

For any non-linear molecule, there are 3N-6 vibrational modes, where N is the number of atoms in the molecule. Here, BH₃ has 4 atoms, and so we predict there to be 6 vibrational modes. These were calculated and are tabulated below:

Wavenumber (cm^-1)	Intensity (arbitrary units)	Symmetry	IR Active?	Type
1163.60	92.48	A2	Yes	Bend (Out of plane)
1213.59	14.08	E'	Yes	Bend
1213.60	14.08	E'	Yes	Bend
2580.15	0	A1'	No	Symmetric Stretch
2713.12	126.40	E'	Yes	Asymmetric Stretch
2713.12	126.39	E'	Yes	Asymmetric Stretch

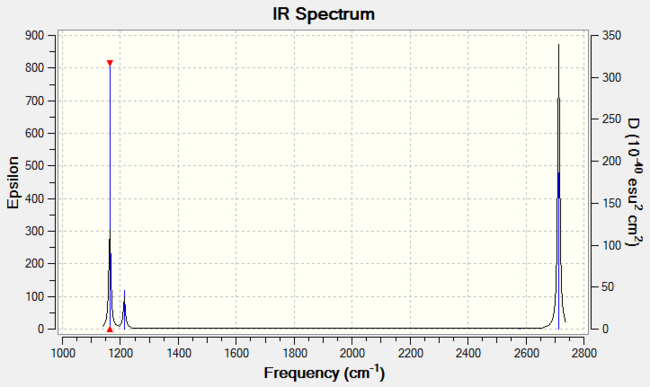
The predicted IR spectrum is as below:

In this spectrum, there only appear to be three peaks, which seems to contradict the number of vibrational modes. However, one of these vibrational modes at 2590 cm^-1 is not IR active. Therefore, 5 of the 6 modes would be expected to be IR active. Of these 5, there are also degenerate vibrational modes at 1214 and 2713 cm^-1. The degeneracy means only 3 peaks are expected on the IR spectrum.

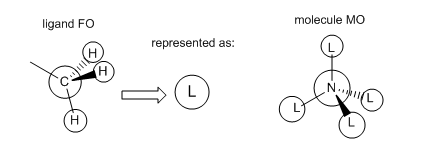
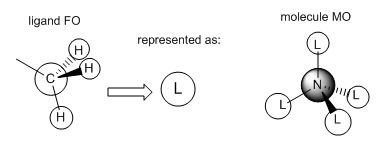
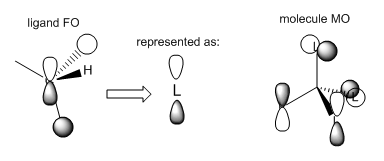
MO diagram of BH₃: Comparison of LCAO and Calculated MOs

The MO diagram for BH₃ is shown below^[1]. The calculated MOs are shown alongside LCAOs for that MO:

As it can be seen, the LCAO to represent the molecular orbitals for this small molecule accurately represents the calculated molecular orbitals. This shows that the qualitative use of MO theory is accurate and useful to describe these systems.

Smf115 (talk) 16:22, 28 May 2018 (BST)Clear inclusion of the MOs on the diagram. While the useful nature of qualitative MO theory has been highlighted, the differences between the calculated and qualitative MOs, such as the difference in AO contirbutions which are particularly visible in 3a₁', could have been discussed.

Ammonia: NH₃

Key Data

The following calculation was performed using a B3LYP/6-31G(d,p) basis set:

Item Table

         Item               Value     Threshold  Converged?
 Maximum Force            0.000013     0.000450     YES
 RMS     Force            0.000006     0.000300     YES
 Maximum Displacement     0.000040     0.001800     YES
 RMS     Displacement     0.000013     0.001200     YES

The file for this calculation is here.

Frequencies

  Low frequencies ---   -8.5223   -8.4750   -0.0037    0.0334    0.1918   26.4067
 Low frequencies --- 1089.7616 1694.1862 1694.1866

Ammonia: NH3

Vibrations for NH₃

For any non-linear molecule, there are 3N-6 vibrational modes, where N is the number of atoms in the molecule. Here, NH₃ has 4 atoms, and so we predict there to be 6 vibrational modes. These were calculated and are tabulated below:

Wavenumber (cm^-1)	Intensity (arbitrary units)	Symmetry	IR Active?	Type
1089.76	145.42	A1	Yes	Bend
1694.19	13.55	E	Yes	Bend
1694.19	13.56	E	Yes	Bend
3461.00	1.06	A1	Almost not	Symmetric Stretch
3589.47	0.27	E	Almost not	Asymmetric Stretch
3589.47	0.27	E	Almost not	Asymmetric Stretch

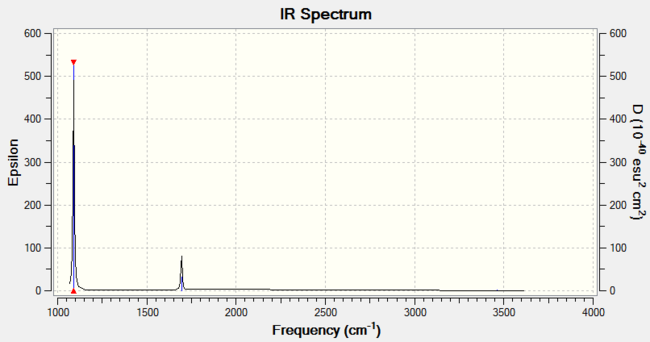
The predicted IR spectrum is as below:

In this spectrum, there only appear to be two peaks, which seems to contradict the number of vibrational modes. However, three of these vibrational modes at 3461 and 3589 cm^-1 very low intensities, and so, when compared to the other vibrational modes, they are practically not IR active. Therefore, 3 of the 6 modes would be expected to be IR active. Of these 3, there is also a degenerate vibrational mode at 1694 cm^-1. The degeneracy means only 2 peaks are expected on the IR spectrum.

Ammonia Borane complex: H₃N-BH₃

Key Data

The following calculation was performed using a B3LYP/6-31G(d,p) basis set:

Item Table

          Item               Value     Threshold  Converged?
 Maximum Force            0.000113     0.000450     YES
 RMS     Force            0.000063     0.000300     YES
 Maximum Displacement     0.000612     0.001800     YES
 RMS     Displacement     0.000351     0.001200     YES

The file for this calculation is here.

Frequencies

 Low frequencies ---   -0.0618   -0.0458   -0.0065   21.6077   21.6136   40.3575
 Low frequencies ---  265.9921  632.3727  640.1263

Ammonia Borane: H3N-BH3

Vibrations for H₃B-NH₃

Wavenumber (cm^-1)	Intensity (arbitrary units)	Symmetry	IR Active?	Type
265.98	0	A2	No	Torsion
632.37	13.99	A1	Yes	Stretch
640.13	3.54	E	Almost not	Rocking
640.13	3.54	E	Almost not	Rocking
1069.48	40.54	E	Yes	Bend
1069.48	40.54	E	Yes	Bend
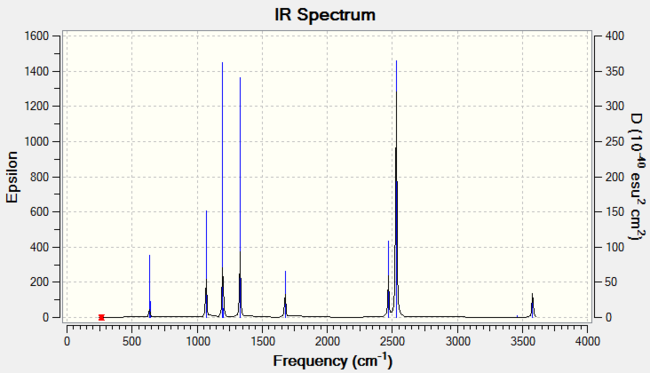
1196.73	108.99	A1	Yes	Bend (out of plane)
1203.60	3.50	E	Almost not	Bend
1203.60	3.50	E	Almost not	Bend
1330.13	113.62	A1	Yes	Bend (out of plane)
1676.63	27.54	E	Yes	Bend
1676.63	27.54	E	Yes	Bend
2470.40	67.27	A1	Yes	Symmetric Stretch
2530.42	231.34	E	Yes	Asymmetric Stretch
2530.42	231.32	E	Yes	Asymmetric Stretch
3462.54	2.51	A1	Almost not	Symmetric Stretch
3579.42	27.92	E	Yes	Aymmetric Stretch
3579.42	27.92	E	Yes	Asymmetric Stretch

The predicted IR spectrum is as below:

Ammonia-Borane Dative Bond Strength

NH₃ + BH₃ → H₃N-BH₃

The strength of the dative covalent B-N bond in this complex can be calculated from the difference in bond energies of the products and the reactants of the above reaction:

$Δ E = E (B - N) = E (H_{3} N B H_{3}) - {E (N H_{3}) + E (B H_{3})}$

E(BH₃) = -26.61532 a.u.

E(NH₃) = -56.55776 a.u.

E(H₃NBH₃) = -83.22469 a.u.

∴ ΔE = E(B-N) = -83.22496 - {-56.55776 - 26.61532} a.u. = -0.05188 a.u. = -136.21 kJ mol^-1

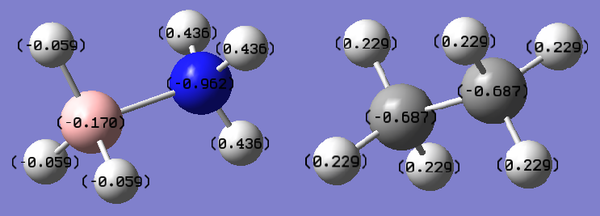
This is a weaker bond than both a N-N single bond (167 kJ mol^-1) and a B-B single bond (293 kJ mol^-1). Dative covalent bonds are weaker than normal covalent bonds, and tend to be polar. in this case, this is because the N atom is more electronegative than the B atom, pulling electron density towards it. This can be seen in comparing the charge distribution in atoms in H₃N-BH₃ (left) with that of an isoelectronic and isostructural molecule, ethane (right).

Ammonia Borane (H₃N-BH₃)
Atom	Charge (arbitrary units)
N	-0.962
H_N	0.436
B	-0.170
H_B	-0.059

Ethane (C₂H₆)
Atom	Charge (arbitrary units)
C	-0.687
H	0.229

Ethane is a very symmetrical molecule (point group D_3d), with the carbon atoms in identical environments, as well as the six hydrogen atoms. Carbon is slightly more electronegative than hydrogen (𝜒_C=2.55, 𝜒_H=2.2), and this is reflected in the charge distribution of the molecule - the carbon atoms have the same negative charge (-0.687), and the hydrogen atoms have the same positive charge (0.229).

In contrast, Ammonia-Borane has reduced symmetry (point group C_3v) because of the difference between the nitrogen and boron atoms involved in the molecule. Nitrogen is more electronegative than boron (𝜒_N=3.04, 𝜒_H=2.04), so the electron density is mostly pulled away from the boron towards the nitrogen atom, hence the higher magnitude of charge on the atom. The high electronegativity of nitrogen also explains the higher charge on the hydrogen atoms bonded to the nitrogen, H_N.

Smf115 (talk) 16:19, 28 May 2018 (BST)Very nice to see the charge analysis between NH₃BH₃ and ethane with good discussion on the relative electrnegativities within the molecules.

Boron Tribromide: BBr₃

Key Data

The following calculation was performed using a B3LYP/6-31G(d,p) basis set for the Boron centre and the LANL2DZ pseudopotential for the Bromide ligands.

The file can be found on DSpace at DOI:10042/202462

Item Table

          Item               Value     Threshold  Converged?
 Maximum Force            0.000008     0.000450     YES
 RMS     Force            0.000004     0.000300     YES
 Maximum Displacement     0.000036     0.001800     YES
 RMS     Displacement     0.000018     0.001200     YES

The file for this calculation is here.

Frequencies

 Low frequencies ---   -0.0137   -0.0064   -0.0047    2.4315    2.4315    4.8421
 Low frequencies ---  155.9631  155.9651  267.7052

Boron Tribromide: BBr3

Vibrations for BBr₃

For any non-linear molecule, there are 3N-6 vibrational modes, where N is the number of atoms in the molecule. Here, BBr₃ has 4 atoms, and so we predict there to be 6 vibrational modes. These were calculated and are tabulated below:

Wavenumber (cm^-1)	Intensity (arbitrary units)	Symmetry	IR Active?	Type
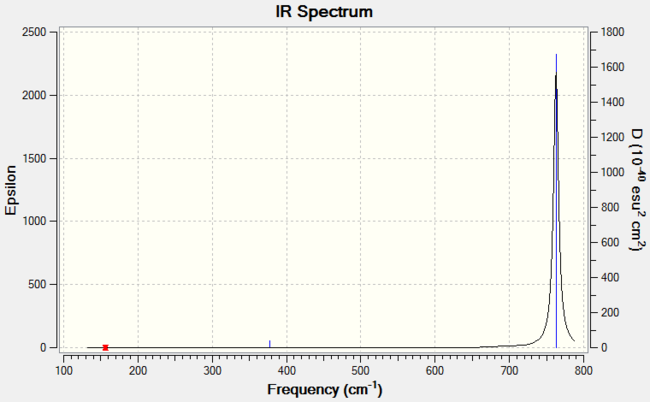
155.96	0.084	E'	No	Bend
155.96	0.084	E'	No	Bend
267.71	0	A1'	No	Symmetric Stretch
377.64	3.65	A2"	No	Bend (Out of plane)
762.84	319.52	E'	Yes	Asymmetric Stretch
762.89	319.55	E'	Yes	Asymmetric Stretch

The predicted IR spectrum is as below:

Ionic Liquids: Designer Solvents

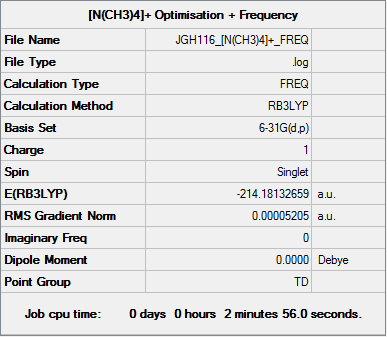
Tetramethylammonium ion: [N(CH₃)₄]⁺

Key Data

The following calculation was performed using a B3LYP/6-31G(d,p) basis set:

Item Table

         Item               Value     Threshold  Converged?
 Maximum Force            0.000091     0.000450     YES
 RMS     Force            0.000052     0.000300     YES
 Maximum Displacement     0.000762     0.001800     YES
 RMS     Displacement     0.000402     0.001200     YES

The file for this calculation is found here.

Frequencies

 Low frequencies ---    0.0010    0.0015    0.0015   35.2559   35.2559   35.2559
 Low frequencies ---  217.2586  316.3846  316.3846

Tetramethylammonium ion

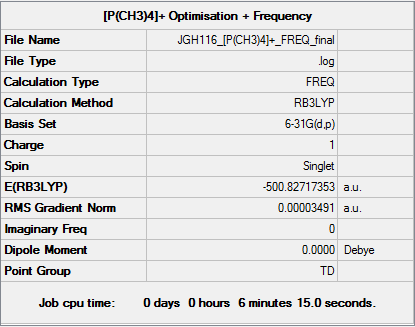
Tetramethylphosphonium ion: [P(CH₃)₄]⁺

Key Data

The following calculation was performed using a B3LYP/6-31G(d,p) basis set:

Item Table

         Item               Value     Threshold  Converged?
 Maximum Force            0.000069     0.000450     YES
 RMS     Force            0.000035     0.000300     YES
 Maximum Displacement     0.000218     0.001800     YES
 RMS     Displacement     0.000114     0.001200     YES

The file for this calculation is found here.

Frequencies

 Low frequencies ---   -0.0009    0.0024    0.0024   50.6093   50.6093   50.6093
 Low frequencies ---  188.2350  213.2379  213.2379

Tetramethylphosphonium ion

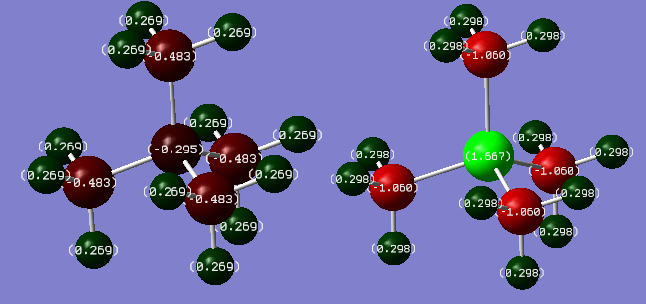
Comparison of Charge Distributions

The charge distributions of the two ions were calculated and are shown below. Green denotes a positive charge, and red denotes a negative charge:

[N(CH₃)₄]⁺
Atom	Charge (arbitrary units)
N	-0.295
C	-0.483
H	0.269

[P(CH₃)₄]⁺
Atom	Charge (arbitrary units)
P	1.667
C	-1.060
H	0.298

These two molecules are analogues, differing only by their central atom. In [N(CH₃)₄]⁺, the N atom has a charge of -0.295, whereas in [P(CH₃)₄]⁺, the P atom has a charge of +1.667. The important difference seen here is the sign of the charge. The N atom has a negative charge on it because it is more electronegative than carbon (𝜒_N=3.04, 𝜒_C=2.55), pulling electron density towards it, away from the carbon atoms. In constrast, the P atom has a positive charge on it because it is less electronegative than carbon (𝜒_P=2.19, 𝜒_C=2.55), therefore the carbon atoms pull electron density away from the P atom, resulting in a large, positive charge.

Carbon is more electronegative than hydrogen (𝜒_C=2.55, 𝜒_H=2.20), and so the carbon atoms in these molecules would be expected to have a negative charge. This is indeed the case in both molecules, with the charge on the carbon atoms in [N(CH₃)₄]⁺ being -0.483, and the charge on the carbon atoms in [P(CH₃)₄]⁺ being -1.060. The charge on the carbon atoms in [P(CH₃)₄]⁺ is over twice that of the carbon atoms in [N(CH₃)₄]⁺ because of the electronegativity of the centres. By inspecting their electronegativitie relative to carbon, (𝜒_N=3.04, 𝜒_P=2.19, 𝜒_C=2.55) the N atom pulls electron density away from the carbon atoms towards itself, whereas the C atoms in [P(CH₃)₄]⁺ pull electron density away from the phosphorus centre reducing their negative charge. Therefore, the charge on the C atoms in [P(CH₃)₄]⁺ is significantly greater in magnitude than the charge on the C atoms in [N(CH₃)₄]⁺.

The hydrogen atoms are two bonds away from the central atom, and are therefore fairly unaffected by the change in the central atom. The net charge on the hydrogen atoms in [N(CH₃)₄]⁺ is 3.228, whereas the net charge on the hydrogen atoms in [P(CH₃)₄]⁺ is 3.576. There is not a significant difference between the two, showing that the change in central atom does not significantly affect the charge on the external atoms.

All electronegativities are from this website.

Tetraalkylammonium ion: [NR₄]⁺

The tetraalkylammonium ion, [NR₄]⁺ is usually depicted with the positive charge localised on the nitrogen centre. The nitrogen atom has four bonds, one more than its usual three bonds and a lone pair. Hence, with a fourth bond, it is logical to place the positive charge on the nitrogen atom. However, the calculated charge distribution of [N(CH₃)₄]⁺ does not reflect this. In this ion, the nitrogen atom carries a slight negative charge of -0.295. This indicates that the psotive charge is not actually localised to the central nitrogen atom, as normally depicted. In fact, the positive charge is distributed evenly and carried by the surrounding hydrogen atoms.

For the phosphorus analogue of the tetraalkylammonium ion (tetraalkylphosphonium), the charge distribution above shows that the central phosphorus atom possesses a positive charge. However, this is surrounded by four carbon atoms each with a negative charge of -1.060. Therefore, the effective positive charge is carried by the surrounding hydrogen atoms.

Smf115 (talk) 19:13, 1 June 2018 (BST)Great charge analysis with details of the electronegativities given and discussed. To improve, while I think you're correct explaining the usual charge depiction on [NMe₄]⁺ it could be a bit clearer explaining it as a result from formal electron counting.

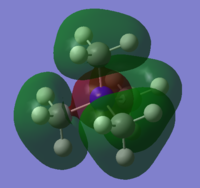
Molecular Orbitals of [N(CH₃)₄]⁺

The molecular orbitals of [N(CH₃)₄]⁺ were calculated and visualised. The valence orbitals were found to start from MO 6, as the energy rose significantly between MOs 5 and 6 from -10...... to -1.19638 a.u. Three of the occupied MOs were visualised and compared to their LCAO approximations below:

Description of MO	Comments	Calculated Energy of MO (a.u.)
MO 6 (Strongly Bonding)	Formed from the overlap of the in-phase s orbitals on all atoms (2s on C and N, 1s on H). This MO is the first valence orbital.	-1.19638
MO 10 (Slightly antibonding)	Formed by the overlap of the in-phase s orbitals of the ligands (2s on C, 1s on H) and the out of phase 2s orbital on N. Despite the ligands being strongly bonding, the 2s orbital on the N centre is out of phase with all the CH₃ ligands FOs, creating many nodes. Therefore, this MO has antibonding character.	-0.80745
MO 16 (Antibonding)	The FO is formed by the in-phase overlap of the C 2p and two H 1s orbitals. The MO is formed from the out of phase combination of these FOs, without any contribution from the central N atom. As there are many out of phase combinations, there are many nodes present in this MO, indicating the MO has significant antibonding character.	-0.58035

Smf115 (talk) 19:10, 1 June 2018 (BST)Good choice of MOs covering a range of character and nice additional comment on the contributions and intro statement on the valence orbitals. The LCAOs and FOs are alrgely correct and clearly presented. However, in MO 16 the FO depicted is correct for the ligands which have no contirbution from one of the hydrogens. Not all four of the CH₃ are the same though and some have contributions from all three of the H's, the corresponding FO for this ligand is then the other e' FO from your BH₃ MO diagram. Therefore, there shoudl actually be two different FOs depicted here, otherwise excellent analysis!

Smf115 (talk) 19:10, 1 June 2018 (BST)Overall, a good wiki report with a strong project section.

References

↑ Dr. P Hunt, Molecular Orbitals Lecture Course, Imperial College London, November, 2017.

[1] Dr. P Hunt, Molecular Orbitals Lecture Course, Imperial College London, November, 2017.

[1]

Borane: BH3

Key Data

Vibrations for BH3

MO diagram of BH3: Comparison of LCAO and Calculated MOs

Ammonia: NH3

Key Data

Vibrations for NH3

Ammonia Borane complex: H3N-BH3

Key Data

Vibrations for H3B-NH3

Ammonia-Borane Dative Bond Strength

Boron Tribromide: BBr3

Key Data

Vibrations for BBr3

Ionic Liquids: Designer Solvents

Tetramethylammonium ion: [N(CH3)4]+

Key Data

Tetramethylphosphonium ion: [P(CH3)4]+

Key Data

Comparison of Charge Distributions

Tetraalkylammonium ion: [NR4]+

Molecular Orbitals of [N(CH3)4]+

References

Borane: BH₃

Vibrations for BH₃

MO diagram of BH₃: Comparison of LCAO and Calculated MOs

Ammonia: NH₃

Vibrations for NH₃

Ammonia Borane complex: H₃N-BH₃

Vibrations for H₃B-NH₃

Boron Tribromide: BBr₃

Vibrations for BBr₃

Tetramethylammonium ion: [N(CH₃)₄]⁺

Tetramethylphosphonium ion: [P(CH₃)₄]⁺

Tetraalkylammonium ion: [NR₄]⁺

Molecular Orbitals of [N(CH₃)₄]⁺