MO:JC5516
MO Joseph Counte
BH3
B3LYP/6-31G(d,p)
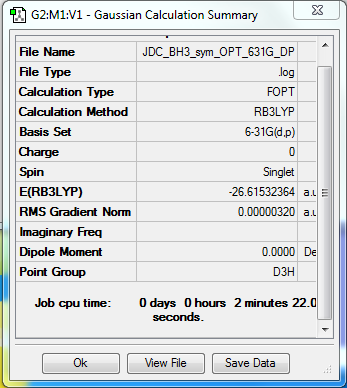
Item Value Threshold Converged?
Maximum Force 0.000006 0.000450 YES
RMS Force 0.000003 0.000300 YES
Maximum Displacement 0.000025 0.001800 YES
RMS Displacement 0.000012 0.001200 YES
Predicted change in Energy=-2.326246D-10
Optimization completed.
-- Stationary point found.
Low frequencies --- -3.9717 -3.7656 -0.0208 0.0004 1.2627 8.9101 Low frequencies --- 1163.0137 1213.1653 1213.1655
BH3 |
BH3 frequencies
Vibrational spectrum for BH3
| wavenumber (cm-1 | Intensity (arbitrary units) | symmetry | IR active? | type |
| 1163 | 93 | A2" | yes | out-of-plane bend |
| 1213 | 14 | E' | very slight | bend |
| 1213 | 14 | E' | very slight | bend |
| 2582 | 0 | A1' | no | symmetric stretch |
| 2716 | 126 | E' | yes | asymmetric stretch |
| 2716 | 126 | E' | yes | asymmetric stretch |
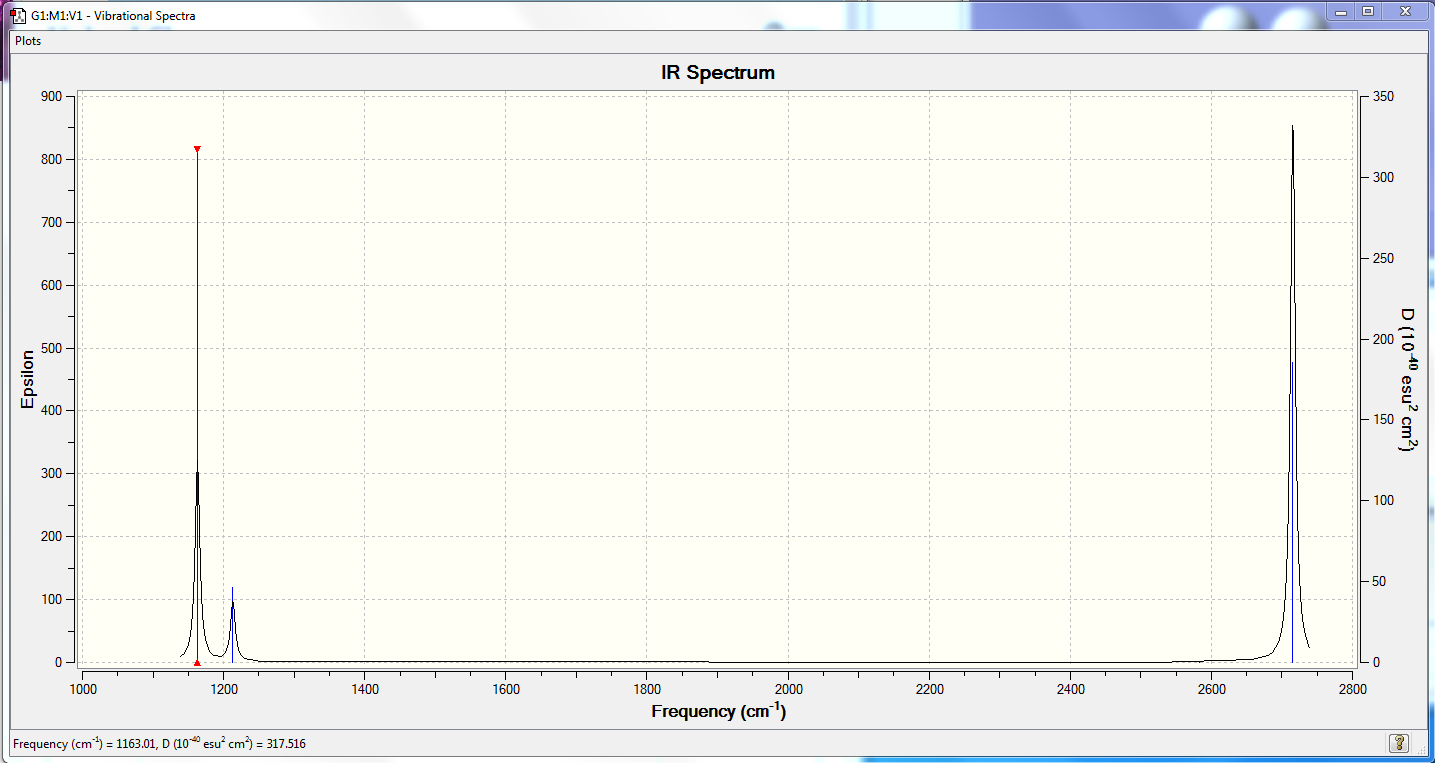
There are only 3 peaks visible on the IR spectrum compared to the 6 distinct modes predicted in the optimization. This is because the 2nd/3rd and 5th/6th modes are doubly degenerate so only 2 peaks are observed where there are 4 modes of vibration. Additionally the 4th mode is a symmetrical stretch in the plane of the molecule which leads to no overall change in dipole moment and hence no absorption intensity is observed.
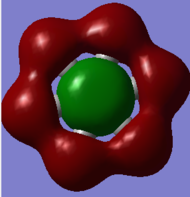
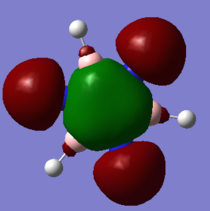
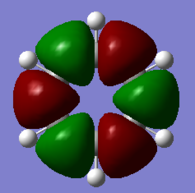
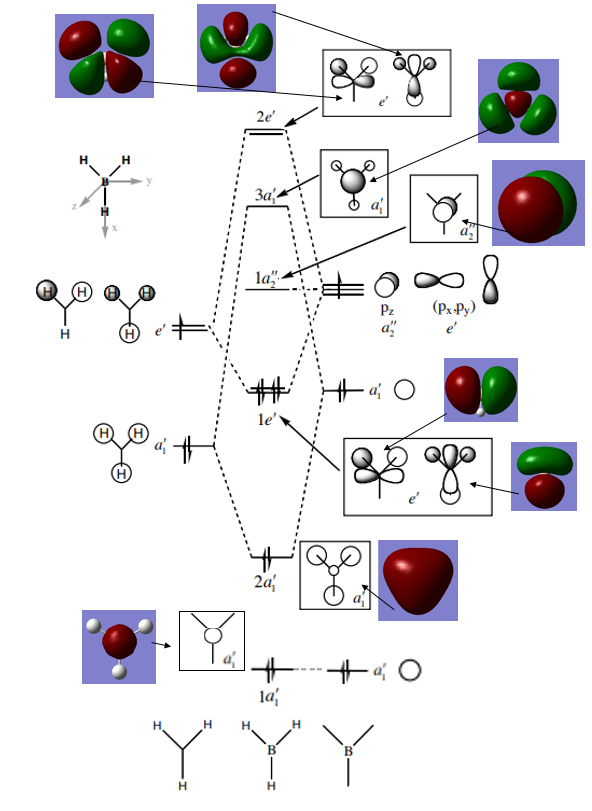
BH3 MOs
reference Tricia
Qualitative LCAO MO theory provides adequate predictions of the 'real' MOs calculated in gaussian with the overall shapes of the MOs being accurate. However the 'real' MOs are have larger orbital sizes and are more diffuse than those predicted with LCAO. in particular the 3a1' MO orbital sizes are not predicted by the LCAO model (the real MO has a larger contribution from the H3 fragment and a smaller size of the B fragment contribution than otherwise predicted.). Overall this indicates that while LCAO qualitative MO theory can predict the overall shapes of MOs correctly it does not accurately predict the relative sizes of electron distribution.
Smf115 (talk) 15:20, 28 May 2018 (BST)Clear inclusion of the MOs on the diagram and good reference to the 3a1' MO to highlight the differences in the relative contributions between the calculated and qualitative MOs.
NH3
B3LYP/6-31G(d,p)
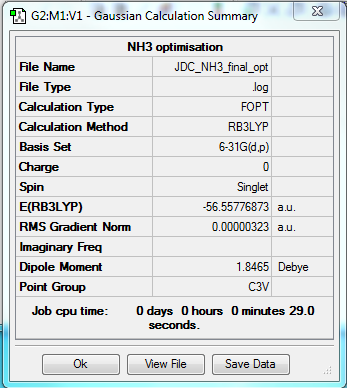
Item Value Threshold Converged?
Maximum Force 0.000006 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000012 0.001800 YES
RMS Displacement 0.000008 0.001200 YES
Predicted change in Energy=-9.843805D-11
Optimization completed.
-- Stationary point found.
Low frequencies --- -0.0138 -0.0032 0.0018 7.0783 8.0932 8.0937 Low frequencies --- 1089.3840 1693.9368 1693.9368
NH3 |
NH3-BH3=
B3LYP/6-31G(d,p)
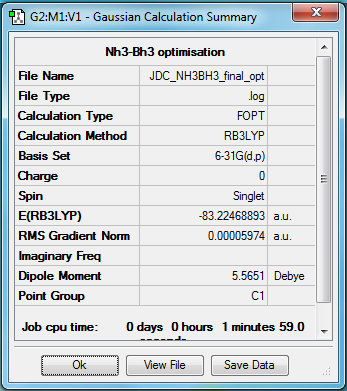
Item Value Threshold Converged?
Maximum Force 0.000123 0.000450 YES
RMS Force 0.000058 0.000300 YES
Maximum Displacement 0.000515 0.001800 YES
RMS Displacement 0.000296 0.001200 YES
Predicted change in Energy=-1.635696D-07
Optimization completed.
-- Stationary point found.
Low frequencies --- 0.0006 0.0011 0.0012 16.8436 17.4462 37.3291 Low frequencies --- 265.8243 632.2043 639.3227
File:JDC NH3BH3 FINAL FREQ.LOG
NH3-BH3 |
Association Energy
E(NH3)= -56.55777 a.u.
E(BH3)= -26.61532 a.u.
E(NH3-BH3)= -83.22469 a.u.
ΔE=E(NH3-BH3)-[E(NH3)+E(BH3)]
ΔE=(-83.22469)-((-56.55777)+(-26.61532)) = -0.05160 a.u.
Association Energy = -135 kJmol-1
Comparatively this is quite a weak bond dissociation energy, for example the C-N bond energy is 308 kJmol-1 and the C=O bond dissocation energy is 799 kJmol-1.[1]
Smf115 (talk) 15:22, 28 May 2018 (BST)Correct calculation and consideration given to the accuracy of the final reported energies. Good referenced comparison which could be improved by highlighting why you chose those two bond energies to compare with.
BBr3
B3LYP/6-31G(d,p)LANL2DZ
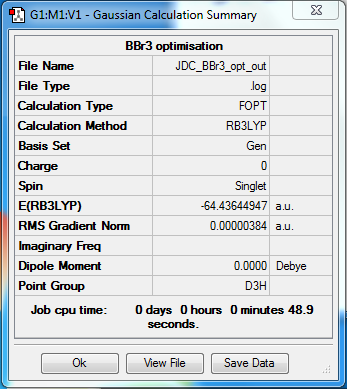
Item Value Threshold Converged?
Maximum Force 0.000008 0.000450 YES
RMS Force 0.000005 0.000300 YES
Maximum Displacement 0.000036 0.001800 YES
RMS Displacement 0.000024 0.001200 YES
Predicted change in Energy=-4.086285D-10
Optimization completed.
-- Stationary point found.
Low frequencies --- -2.3055 -0.0029 -0.0018 0.0774 0.7534 0.7534 Low frequencies --- 155.9402 155.9405 267.6894
BBr3 |
Aromaticity project
Benzene
B3LYP/6-31G(d,p) File:JDC BENZENE FREQ.LOG
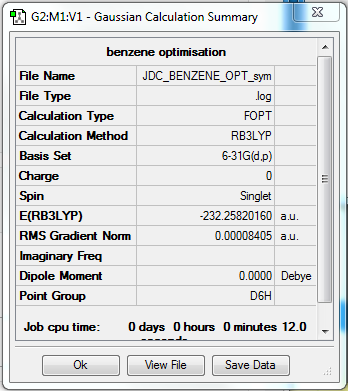
Item Value Threshold Converged?
Maximum Force 0.000194 0.000450 YES
RMS Force 0.000077 0.000300 YES
Maximum Displacement 0.000824 0.001800 YES
RMS Displacement 0.000289 0.001200 YES
Predicted change in Energy=-4.246203D-07
Optimization completed.
-- Stationary point found.
Low frequencies --- -16.9682 -14.6636 -14.6636 -0.0057 -0.0056 -0.0016 Low frequencies --- 414.1239 414.1239 620.9400
NH3-BH3 |
Borazine
B3LYP/6-31G(d,p) File:JDC BORAZINE FREQ.LOG
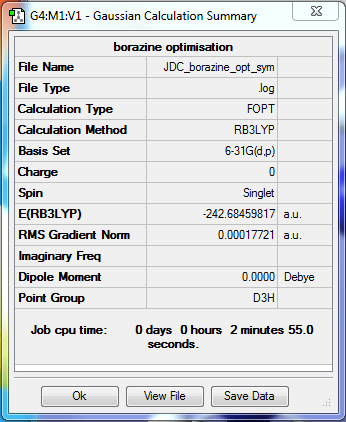
Item Value Threshold Converged?
Maximum Force 0.000172 0.000450 YES
RMS Force 0.000079 0.000300 YES
Maximum Displacement 0.000705 0.001800 YES
RMS Displacement 0.000251 0.001200 YES
Predicted change in Energy=-7.354757D-07
Optimization completed.
-- Stationary point found.
In the frequency analysis the point group is converted to C2V due to inaccuracies in Gaussian however the frequencies recorded are still thought to be correct.
Low frequencies --- -0.0008 0.0004 0.0011 5.4370 6.0114 8.0002 Low frequencies --- 289.8759 289.9500 404.4254
Borazine |
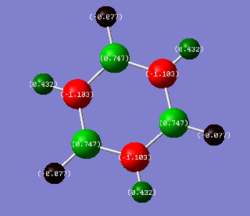
charge distribution
| Benzene | Comment |
|---|---|
 |
In benzene the carbons all have a charge of -0.239 and all hydrogen shave a charge of 0.239 with all charges summing to 0. |
| Borazine | Comment |
|---|---|
 |
In borazine the Nitrogen atoms all have a charge of -1.103 and all borons have a charge of 0.747. The hydrogens bonded to nitrogen have a charge of 0.432 and the boron bonded hydrogens have a charge of -0.077. All charges sum to zero |
Comparison
Benezene displays a symmetrical charge distribution due to the ring atoms all being equivalent and having the same Pauling electronegativity, thus the distribution of charge comes from the difference in electronegativity between the hydrogens and the carbons (C: 2.5 vs H: 2.1). These similar electronegativities between carbon and hydrogen account for why the charges present on the atoms are less when compared to borazine. In borazine the nitrogens have a very large negative charge which corresponds to its large Pauling electronegativity value of 3.07, Boron has a low electronegativity value of 2.01 which is why the charge is positive on boron atoms[2], the difference in ring atom charges is further altered when the hydrogens are present. from a qualitative perspective in borazine, boron too will be electron deficient owing to it's empty p orbital, wheres nitogen has a full valence shell of 8 electrons.
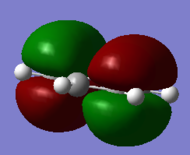
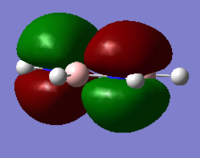
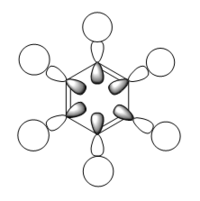
Comparative MOs
| Benzene | Borazine | LCAO | Analysis |
|---|---|---|---|
 |
 |
 |
MO 20 from benzene and MO 21 from borazine share the same orbital phase pattern with a nodal plane along the two centre atom of the ring perpendicular to the plane of the molecule. Additionally the nodal plane in the plane of the molecule corresponds to the symmetry observed in Pz atomic orbitals. The two centre atoms exhibit non bonding character. The two MOs are comparatively high in energy for bonding MOs(with the borazine one being the HOMO for the molecule). This can be explained by the through space antibonding interactions between the two opposite phase Pz orbital regions. |
 |
 |
 |
MO 12 from benzene and MO 10 from borazine both show a central area of electron density surrounded by a region of opposite electron density. The ring atoms display a change in phase of the electron density which is characteristic of py/px orbitals along the plane of the ring atom to hydrogen bond. In benzene there is a large bonding through space interaction and overlap with the outer hydrogen 1s and ring atom 2p orbitals to form a continuous ring of electron density. This is not observed in borazine possibly due the nitrogen atoms having concentrated charge density in the molecule leaving little electron density for the boron atom equivalent. overall this is a deep in energy bonding MO due to the strong through space overlap and few nodes in the molecule. |
 |
 |
 |
MO 14 from benzene and MO 15 from borazine display an identical alternating electron phase pattern from bond to bond in the ring. There is a phase change at every atom in each ring which resembles overlapping px/y atomic orbitalsin the plane of the molecule. These Mos are also deep in energy due to the strong in phase directional overlap of the p orbitals making this molecule weakly bonding overall despite the 6 nodes. The borazine MO is slightly less symmetric than the benzene equivalent as the size of the nodes on the atoms vary from boron to nitrogen. |
Smf115 (talk) 11:49, 1 June 2018 (BST)Nice selection of comparable orbitals for the MO analysis and good inclusion of the LCAO diagrams. However, MO 12 and MO 10 will have slightly different LCAOs due to the difference in the contributions between them. The comparison is good but more detail could be included, such as whether the MOs are pi- or sigma- type, symmetry differences or clearer evaluation of the bonding/anti-bonding character.
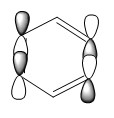
Aromaticity
Traditionally aromaticity was defined as a stabalised planar 4n+2 pi electron system with electrons delocalised in a contiguous array of p orbitals. The special stabilisation of benzene was thought to come from its's aromaticity with each carbon atom in the ring structure contributing 1 electron from the pz orbitals arranged orthogonal to the ring. This definition was then extended to other heteroaromatic compounds such as pyridine and furan and would be applicable to the isoelectronic borazine. However with with the advent of advanced quantum mechanics and MO theory it is becoming apparent that there are multiple different types of aromaticity. As of September 2016 there are at least 45 different concepts of aromaticity, some expousing the idea that aromaticity can exist in 3D, for example in polyhedral boranes. [3] Aromaticity does not have to exclusively detail pi electron behavior, some systems have considered that sigma bonding framework may also contribute to aromatic character in saturated inorganic rings.[4] Purely taking into account the overlap of pz orbitals in benzene to explain aromaticity can be seen to be insufficient as a wide range of other MOs(some of which discussed above) must also contribute to the overall energy of the molecule and the subsequent electron distribution. Other pi interactions and sigma bonding framework must be considered to contribute to the total special stabalisation of the molecule. Although essentially a qualitative concept efforts to detail aromaticity can look at The nucleus-independent chemical shifts at ring centers (NICS) and ring current density maps to asses structural, energetic, and magnetic aromaticity. When taken together new evidence shoes the traditional pz orbital approach is increasingly becoming a poor descriptor for aromatic compounds.
Smf115 (talk) 11:56, 1 June 2018 (BST)Nice examples used to illustrate the changing definitions of aromaticity and numerous points included in the discussion. To improve, all examples should be referenced and the answer needs to be developed further. While a lot of points are mentioned they are all very brief and should be discussed more and used to clearly explain why the overlapping pZ AO picture is a bad descriptor.
Smf115 (talk) 11:56, 1 June 2018 (BST)Overall a good wiki report with a decent attempt at the project section which just lacked some further discussion in places.
References
- ↑ 1.0 1.1 Huheey, pps. A-21 to A-34; T.L. Cottrell, "The Strengths of Chemical Bonds," 2nd ed., Butterworths, London, 1958
- ↑ 2.0 2.1 A complete table of electronegativities" Elbert J. Little Jr. and Mark M. Jones,Journal of Chemical Education, 1960, 37 (5), 231,
- ↑ 3.0 3.1 Grunenberg J. Ill-defined chemical concepts: The problem of quantification. Int J Quantum Chem. 2017;117:e25359.
- ↑ 4.0 4.1 J. Phys. Chem. A 109, 16, 3711-3716