MM:WJB115
NH3 Molecule
I have investigated the energetics of the haber-process by optimising NH3, N2 and H2 molecules. Then I extracted molecular information: charge, bond length and vibrational properties. When investigating a molecule of Cl2 the same molecular information was found. In addition to this I looked at the molecular orbitals in Cl2 and the relevant atomic orbitals.
Summary
Calculation method:RB3LYP
Basis set: 6-31G(d.p)
Final Energy= -56.55776873 a.u.
RMS Gradient= 0.00000485 a.u.
Point group= C3V
Item
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES
Dynamic Image
Optimised NH3 |
The optimisation file is liked to here
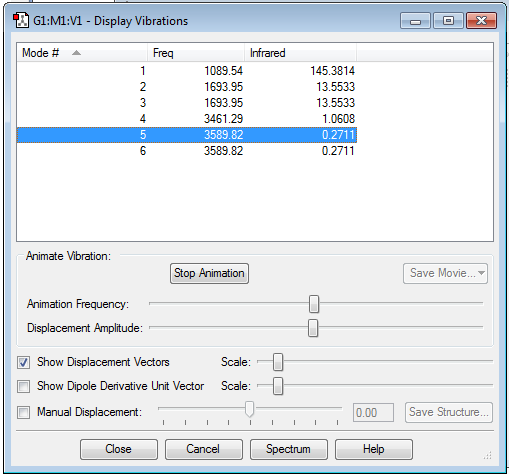
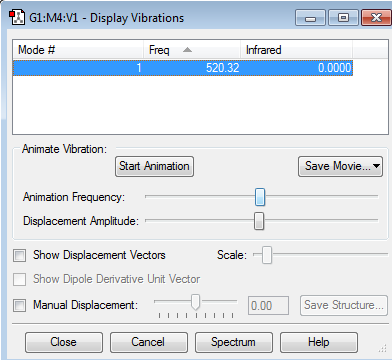
Display Vibrations
Questions
how many modes do you expect from the 3N-6 rule? 6
which modes are degenerate (ie have the same energy)? 2&3 5&6
which modes are "bending" vibrations and which are "bond stretch" vibrations? bending=1,2,3 bond stretch=4,5,6
which mode is highly symmetric? 4
one mode is known as the "umbrella" mode, which one is this? 1
how many bands would you expect to see in an experimental spectrum of gaseous ammonia? 2 since there are two distinct frequencies for the 6 modes therefore one would expect 2 bands. Two of the frequencies have a small value on the y-axis (relative intensity) which would make them hard to identify. These small intensities are due to a small change in dipole moment.
Charge distribution on ammonia
Charge on N=-1.125
Charge on Hydrogen=0.375
Nitrogen is more electronegative so will have the more negative charge
H-N-H bond angle
Optimized bond angle=105.741
N-H bond distance
Optimized bond distance=1.01798
N2 Molecule
Summary
Calculation method:RB3LYP
Basis set: 6-31G(d.p)
Final Energy= -109.524 a.u.
RMS Gradient= 0.00001902 a.u.
Point group= DinfH
Bond distance= 1.10550 Å
Charge:0 because both the atoms have the same electronegativity
Item
Item Value Threshold Converged? Maximum Force 0.000033 0.000450 YES RMS Force 0.000033 0.000300 YES Maximum Displacement 0.000010 0.001800 YES RMS Displacement 0.000015 0.001200 YES
Dynamic Image
Optimised N2 |
The optimisation file is liked to here
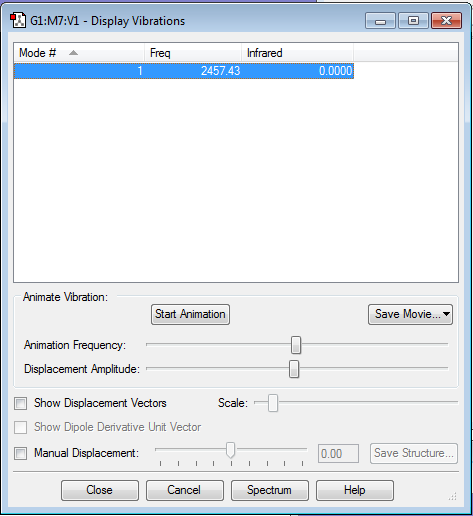
Display vibrations
The frequency was not negative
H2 molecule
Summary
Calculation Method RB3LYP
Basis Set: 6-31G(d,p)
Energy E(RB3LYP) -1.17853929 a.u.
RMS Gradient Norm 0.00012695 a.u.
Point Group D*H
Bond Distance=0.74279 Å
Charge:0 both atoms have the same electronegativity
Item
Item Value Threshold Converged? Maximum Force 0.000220 0.000450 YES RMS Force 0.000220 0.000300 YES Maximum Displacement 0.000289 0.001800 YES RMS Displacement 0.000408 0.001200 YES
Dynamic Image
Optimised H2 |
The optimisation file is liked to here
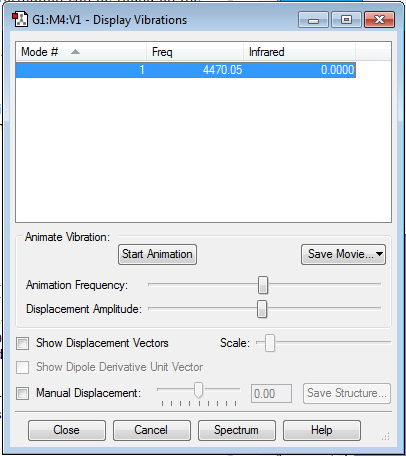
Display Vibrations
Energy of Haber Process Reaction
Energies in atomic units
E(NH3)= -56.55776873
2*E(NH3)= -113.1155375
E(N2)= -109.524
E(H2)= -1.17853929
3*E(H2)= -3.53561808
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.05579074
In kJ/mol ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -146.4785879
The product is more stable
Cl2 Molecule
Summary
Calculation Type FREQ
Calculation Method RB3LYP
Basis Set 6-31G(d,p)
Charge 0
Spin Singlet
E(RB3LYP) -920.34987886
RMS Gradient Norm 0.00002510
Point Group D*H
Charge of Cl2 molecule
The two Cl atoms have the same electronegativity so the molecule is neutrally charged
Item
Item Value Threshold Converged? Maximum Force 0.000043 0.000450 YES RMS Force 0.000043 0.000300 YES Maximum Displacement 0.000121 0.001800 YES RMS Displacement 0.000172 0.001200 YES
Dynamic Image
Optimised Cl2 |
Link to optimised file here
Display vibrations
The infrared=0 because there is no change in dipole across the molecule
Molecular Orbitals of Cl2

|
2px π bonding MO |
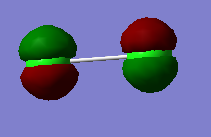
|
2px orbitals result in π* anti-bonding MO |
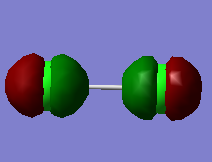
|
2pz σ bonding MO, caused by the overlap of 2p orbitals in z orientation |
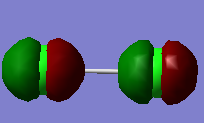
|
2p orbitals result in σ* Anti-bonding MO |
|
2s σ* Anti-bonding MO |
LUMO
The LUMO is the result of two out of phase 3pz orbitals creating a σ* anti-bonding MO
HOMO
The HOMO is a π* bonding MO due to the 3px and 3py orbitals, which give two degenerate molecular orbitals.