MM2athena
NH3 Molecule
| Molecule Name | NH3 |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| final energy E(RB3LYP) in atomic units (au) | -56.55776873 |
| Point Group | C3V |
Item Table
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000072 0.001800 YES
RMS Displacement 0.000035 0.001200 YES
This is my link [1]
test molecule |
N-H bond length : 1.02 Å error: 0.01 Å
H-N-H bond angle : 106o error: 1°
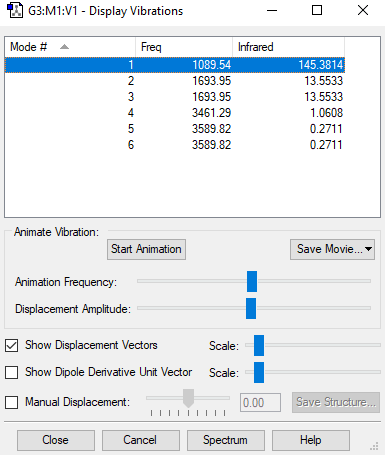
Vibrational analysis
| wavenumber cm-1 |
1090 | 1694 | 1694 | 3461 | 3590 | 3590 |
| symmetry | A1 | E | E | A1 | E | E |
| intensity arbitrary units |
145 | 14 | 14 | 1 | 0 | 0 |
| image | 
|
|
|
|
|
|
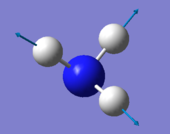
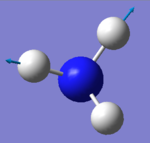
- Number of modes expected using 3N-6 rule : 6
- Degenerated Modes : 2 modes of wavenumber 1694cm-1 and 2 of wavenumber 3590 cm-1
- "bending" vibrations: 1090 cm-1 , 1694 cm-1 (both of them)
- "bond stretch" vibrations: 3461cm-1 and 3590 cm-1 (both of them)
- Highly symmetric mode: 3461 cm-1
- Umbrella mode: 1090 cm-1
- Expected number of bands in experimental spectrum of gaseous ammonia: In the IR spectrum we need to see a change in dipole moment so we would expect 3 but we see only 2 ( 1090 cm-1 , 1694 cm-1) because 2 of the modes are degenerated. The ones with intensity 0 are not show and also the vibrational mode of wavenumber 3461 cm-1 does not have a change in dipole moment(it is symmetrical)
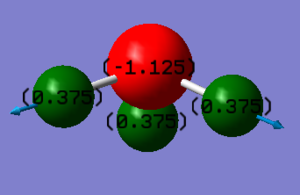
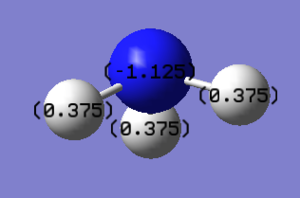
Charge Distribution:
Nitrogen (N) is more electronegative and pulls electron density away from than Hydrogen (H) therefore the expected charge on Nitrogen will be negative and the one on Hydrogen positive. Since there are three H atoms present and the molecule is neutral, the charge on the Nitrogen will be three times the charge of each hydrogen atom
Expectation is in agreement with our calculations.
According to calculations charge on Nitrogen is -1.125 and charge on a hydrogen atom is +0.375
N2 Molecule
| Molecule Name | N2 |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| final energy E(RB3LYP) in atomic units (au) | -109.52412868 |
| Point Group | D*H |
Item Table
Item Value Threshold Converged? Maximum Force 0.000001 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES
This is my link [2]
test molecule |
Bond Length: 1.11 Å error: 0.01 Å
Bond Angle: 180o error 1o
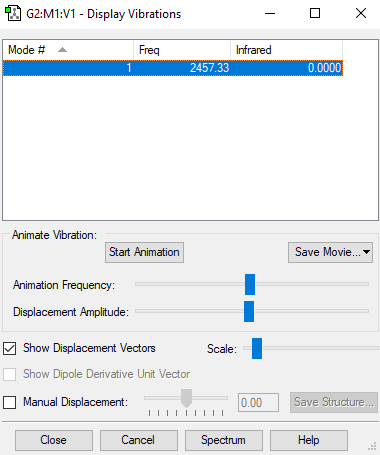
Vibrational analysis
| wavenumber cm-1 |
2457 |
|---|---|
| symmetry | SGG |
| intensity arbitrary units |
0 |
| image |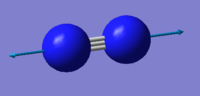 
|
- Number of modes expected using 3N-5 rule : 1
- Degenerated Modes : 0
- "bending" vibrations: 0
- "bond stretch" vibrations: 2457 cm-1
- Highly symmetric mode: 2457 cm-1
- Umbrella Mode: -
- Expected number of bands in experimental spectrum :0 (no dipole moment)
Charge Distribution:
The Homonuclear diatomic molecule is neutral and since it is consisted of two Nitrogen(N) atoms, each one of them has charge of zero
Expectation is in agreement with our calculations.
According to calculations charge on each Nitrogen atom is 0
Mono-metallic Transition Metal complex
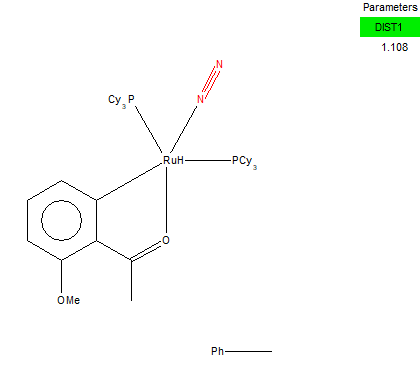
From Research at ConQuest, one transition metal complex that containes H2 is the one linked here [[3]]
Unique Identifier : YECMOL
The distance between the two Nitrogen atoms in the metal complex is 1.108 Å. When the bond distance of two nitrogen atoms was calculated it was found to be 1.10550 Å ( with all d.p). The small difference present indicates that the bond between the 2 nitrogens in the metal complex is longer than the bond we calculated in the optimised structure. This is because the electron density at the N≡N homonuclear diatomic molecule is distributed evenly between the two atoms whereas in the complex, the electron density is pulled away from the bond between the nitrogens and goes towards the bond of the one nitrogen with the transition metal. This makes the bond of N≡N weaker therefore longer than the one in the N≡N molecule. Comparing the optimised bond distance to the crystal structure bond distance in 2 d.p. though, we can see that they are exactly the same. We should therefore take into account errors which possibly occured from the computational calculation method. If the bond distance of N≡N was determined experimentally it would have been more accurate and probably shorter. To get a bigger difference between the bond lengths one way would be to optimise the optimised molecule, and then repeat the procedure. This time we could improve the accuracy by using a better computational method (not RB3LYP) that has more parameters to optimise.
H2 Molecule
| Molecule Name | H2 |
|---|---|
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| final energy E(RB3LYP) in atomic units (au) | -1.17853936 |
| Point Group | D*H |
Item Table
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000001 0.001200 YES
This is my link [4]
test molecule |
Bond Length: 0.75 Å (2 d.p) error: 0.01 Å
Bond Angle: 180o error: 1o
Vibrational analysis
| wavenumber cm-1 |
4466 |
|---|---|
| symmetry | SGG |
| intensity arbitrary units |
0 |
| image |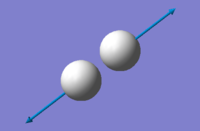 
|
- Number of modes expected using 3N- rule : 1
- Degenerated Modes : 0
- "bending" vibrations: 0
- "bond stretch" vibrations: 4466 cm-1
- Highly symmetric mode: 4466 cm-1
- Umbrella mode: -
- Expected number of bands in experimental spectrum: 0 (no dipole moment)
Charge Distribution:
The homonuclear diatomic molecule is neutral and since it is consisted of two Hydrogen(H) atoms, each one of them has charge of zero
Expectation is in agreement with our calculations.
According to calculations charge on each hydrogen atom is 0
Mono-metallic Transition Metal complex
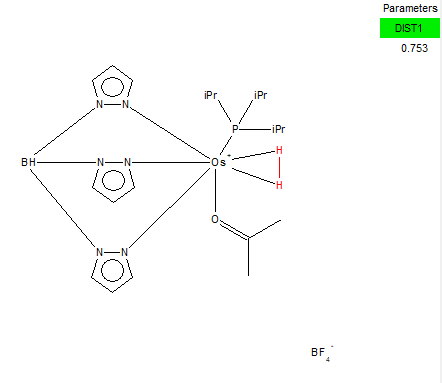
From Research at ConQuest, one transition metal complex that containes H2 is the one linked here [[5]]
Unique Identifier: CILXAX
The exact bond distance calculated for the H-H bond was 0.74279 Å. The bond distance of the same bond in the transition metal complex is 0.753 Å. The small difference present indicates that the bond between the 2 hydrogens in the metal complex is longer than the bond we calculated in the optimised structure. This is because the electron density at the H-H homonuclear diatomic molecule is distributed evenly between the two atoms whereas in the complex, the electron density is pulled away from the bond between the H atoms and goes towards the bonds that these hydrogens form with the transition metal . This makes the bond of H-H weaker therefore longer than the one in the H-H molecule. Comparing the optimised bond distance to the crystal structure bond distance in 2 d.p. though, we can see that they are exactly the same. We should therefore take into account errors which possibly occured from the computational calculation method. To get a bigger difference between the bond lengths one way would be to optimise the optimised molecule, and then repeat the procedure. This time we could improve the accuracy by using a better computational method (not RB3LYP) that has more parameters to optimise. This would result in a larger difference between the bond lengths of the two ( H-H, and transition metal complex of H-H)
Haber-Bosch process
N2 + 3H2 -> 2NH3
E(NH3)= -56.55776873 au (7 d.p.)= - 148492.421 kJmol-1
2*E(NH3)= -113.1155375 au (7 d.p.)=-296984.8437 kJmol-1
E(N2)=-109.52412868 au (7 d.p.)= - 287555.5998 kJmol-1
E(H2)= -1.17853936 au (7 d.p.)=-3094.25509 kJmol-1
3*E(H2)= -3.53561808 au ( 7 d.p.)= - 9282.765269 kJmol-1
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.0557907 au
ΔE=-146.5 (1 d.p) kJmol-1
The products are lower in energy than the reactants ( Energy has a more negative value) therefore they are more stable. The reaction towards the products is more thermodynamically feasible because ΔG is negative.
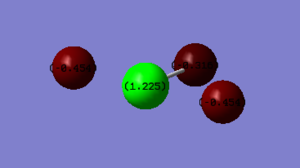
ClF3
| Molecule Name | Clf3 |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| final energy E(RB3LYP) in atomic units (au) | -759.46531688 |
| Point Group | CS |
Item Table
Item Value Threshold Converged? Maximum Force 0.000072 0.000450 YES RMS Force 0.000032 0.000300 YES Maximum Displacement 0.000232 0.001800 YES RMS Displacement 0.000142 0.001200 YES
This is my link [6]
test molecule |
Bond Lengths: 1.73 Å (Cl-F3), 1.73 Å (Cl-F4), 1.65 Å (Cl-F2) (in 2 d.p) error: 0.01 Å
Bond Angles : 87o (F2-Cl-F3) , 87o (F2-Cl-F4), 174 o (F3-Cl-F4) (O d.p) error: 1o
The bond angles seem absurd because the correct structure of the molecule is T-shaped because the 2 lone pairs on Chlorine are in the equatorial position. Therefore the bond angles should have been 90 between F-Cl-F and 180. The difference is because the angles were calculated using computational methods. Therefore there are possible errors that might occur. To get the correct values of angles one way would be to optimise the optimised molecule, and then repeat the procedure. This time a more accurate calculation method could be used (not RB3LYP) that has more parameters to solve.
However, if one searches for all the possible angles of this molecule there are many values found on the web. For example [[7]].
Also according to other sources for example [[8]] the shape is T-shape but due to the lone pair repulsions the F–Cl–F angle is less than 180°.
Vibrational analysis
| wavenumber cm-1 |
305 | 309 | 401 | 541 | 736 | 753 |
|---|---|---|---|---|---|---|
| symmetry | A' | A | A' | A' | A' | A' |
| intensity arbitrary units |
14 | 18 | 2 | 3 | 38 | 370 |
| image |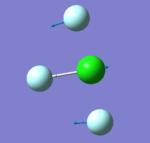 
|
|
|
|
|
|
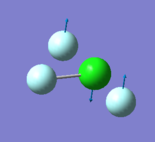
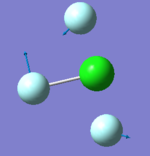
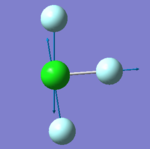
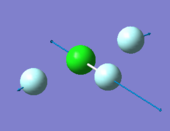
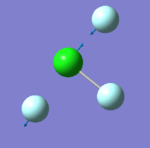
- Number of modes expected using 3N-6 rule : 6
- Degenerated Modes : 0
- "bending" vibrations: 305 cm-1 , 309 cm-1 , 401 cm-1
- "bond stretch" vibrations: 541 cm-1, 736 cm-1 , 753 cm-1
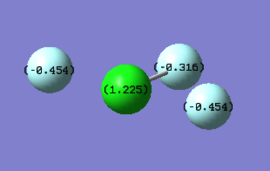
Charge Distribution:
Fluorine atoms are more electronegative than the Chlorine atom therefore they withdraw electron density away from it. Also the 2 fluorine atoms have about the same distance from the centre atom therefore they will have the same charge and the other one a bit different one. All of their charges are negative. The sum of all the charges on atoms should be negative therefore chlorine has a positive charge with magnitude equal to the sum of the negative charges on fluorine atoms.
Expectation is in agreement with our calculations.
According to calculations charge on Chlorine is + 1.125
Charge of each fluorine atoms that has a bond distance 1.73 Å from the chlorine atom : -0.454
Charge of fluorine atom of bond distance 1.65 Å : -0.316
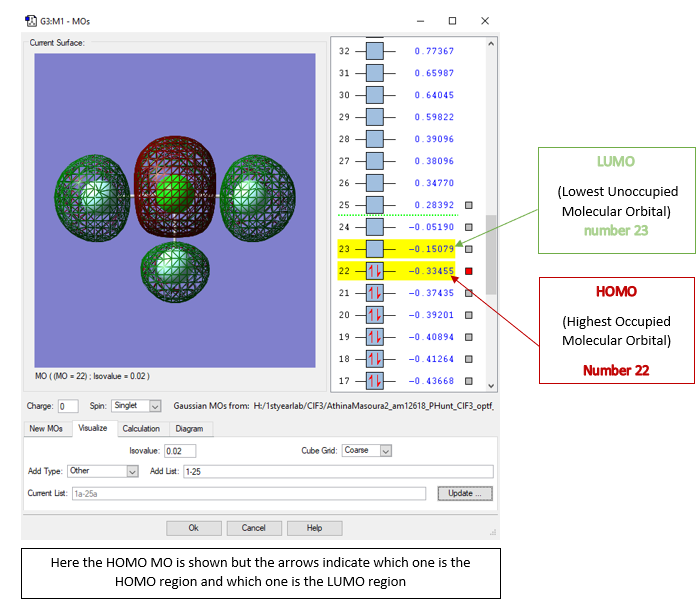
Molecular Orbitals
The Orbitals shown are the solutions to the Schrödinger equation [9]
| Molecular Orbital | 1 | 9 | 10 | 13 | 15 |
|---|---|---|---|---|---|
| Character of MO | The energy of MO is -101.79317 au. This means that the orbitals of Cl, F1, F2, and F3 are very deep in energy. The electrons are very close to the nucleus-They are very deep in core, so the orbitals are not involved in bonding. | The energy of the MO is -1.28165 au. Here we can visualize the s orbitals of all the atoms (as spheres) overlapping. The MO is bonding so all the s orbitals overlap together to form bonds.
The MO is occupied |
The energy of the MO is -1.17371 au. What is shown is the p orbitals (parallel) of F3 and Cl overlapping.The same p atomic orbital of Cl is overlapping with a p orbital of F4. These are all bonding orbitals, whereas the s orbital of F2 is antibonding to the s orbital of chlorine.Consequently the MO is a mixture of bonding and antibonding. ( we can see a nodal plane- electrons are not along the bond)
The MO is occupied |
The energy of the MO is -0.59476 au. Here, a p orbital of the F3 overlaps with the p orbital of Chlorine. The p orbitals are parallel. Also, that p orbital of Cl overlaps with one p orbital of F4 that is parallel to it. These are all bonding orbitals.There are sigma interactions along the bonds. However there is an antibonding orbital between the s orbital of the F2 atom and the p orbital of Cl. Consequently the MO is a mixture of bonding and antibonding. ( we can see a nodal plane- electrons are not along the bond).
The MO is occupied |
The energy of the MO is -0.53821 au. Here all the parallel p atomic orbitals of all the atoms overlap with each other resulting in a bonding MO. We see a nodal plane because of the nodal plane present in the p orbitals when there is change of phase.
The MO is occupied |
| Image | 
|
|
|
|
|
Marking
Note: All grades and comments are provisional and subject to change until your grades are officially returned via blackboard. Please do not contact anyone about anything to do with the marking of this lab until you have received your grade from blackboard.
Wiki structure and presentation 0.5/1
Is your wiki page clear and easy to follow, with consistent formatting?
YES
Do you effectively use tables, figures and subheadings to communicate your work?
YES, overall good, but you have left all the jmol captions as the default “test molecule” this gives the reader no information.
NH3 1/1
Have you completed the calculation and given a link to the file?
YES
Have you included summary and item tables in your wiki?
YES
Have you included a 3d jmol file or an image of the finished structure?
YES
Have you included the bond lengths and angles asked for?
YES
Have you included the “display vibrations” table?
YES
Have you added a table to your wiki listing the wavenumber and intensity of each vibration?
YES
Did you do the optional extra of adding images of the vibrations?
YES
Have you included answers to the questions about vibrations and charges in the lab script?
YES
N2 and H2 0/0.5
Have you completed the calculations and included all relevant information? (summary, item table, structural information, jmol image, vibrations and charges)
YES, However you have given a bond angle of 180 for N2 and H2, there are no bond angles in diatomic molecules. Bond angles involve exactly 3 atoms.
Crystal structure comparison 0.5/0.5
Have you included a link to a structure from the CCDC that includes a coordinated N2 or H2 molecule?
YES
Have you compared your optimised bond distance to the crystal structure bond distance?
YES, good detailed explanation, well done!
Haber-Bosch reaction energy calculation 1/1
Have you correctly calculated the energies asked for? ΔE=2*E(NH3)-[E(N2)+3*E(H2)]
YES
Have you reported your answers to the correct number of decimal places?
YES
Do your energies have the correct +/- sign?
YES
Have you answered the question, Identify which is more stable the gaseous reactants or the ammonia product?
YES
Your choice of small molecule 4.5/5
Have you completed the calculation and included all relevant information?
YES, in general most molecules are not shaped exactly perfect. This is often due to a principle call Jahn-Teller distortion, you will learn more about this later!
Have you added information about MOs and charges on atoms?
YES, very good effort with your explanations, well done for explaining the impact of the interactions between the AOs on the bonding in the molecule. MO 10 is actually s orbitals, not p, and MO13 is all p orbitals. The F-Cl interactions are bonding, there are no nodes across the bonds, the node is at the F atom because it has a p orbital.
Independence 1/1
If you have finished everything else and have spare time in the lab you could:
Check one of your results against the literature, or
Do an extra calculation on another small molecule, or
Do some deeper analysis on your results so far
You looked up and added extra details from the literature, well done!