MDR:Physical Comp Lab Francesca Wittmann 01330365
Exercise one
Question One
On a potential energy surface diagram, how is the transition state mathematically defined? How can the transition state be identified, and how can it be distinguished from a local minimum of the potential energy surface?
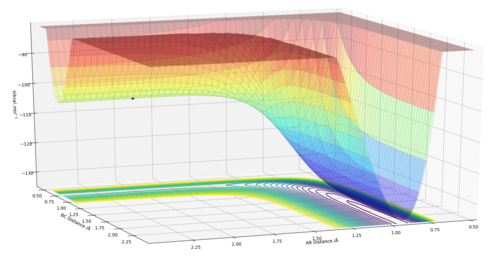
The transition state is the point along the reaction trajectory which is a saddle point of potential energy. I.e it is a point where there is simultaneous a maximum and minimum potential energy. At a saddle point the gradient (first derivative) along both axes is zero.
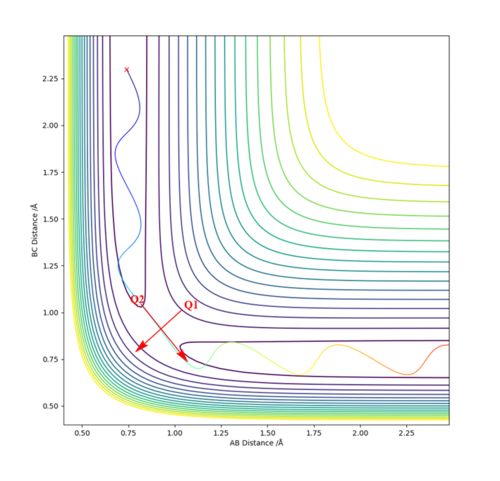
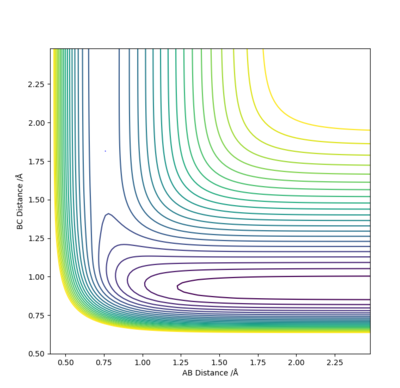
In order to identify where the saddle point is on a potential energy surface diagram, two orthogonal functions are defined. The function Q1 is the potential energy with respect to the line that is orthogonal to the max potential energy point along the minimum energy pathway(see multicoloured squiggly line on diagram). Function Q2 is the potential energy with respect to the line that is tangential to the max potential energy along the minimum energy pathway.
To find the saddle point, you would differentiate along both Q1 and Q2. There should be a point where Q2 is at a maximum whilst Q1 is simultaneously at a minimum. At this point:
δV/δQ1=δV/δQ2=0 and δV2/δQ12 >0 and δV2/δQ22 <0
A local minimum will not have the lowest potential energy on a global (i.e. total range) scale. Firstly you would differentiate across the whole range to find anywhere that had a potential gradient of 0 to find all of the minima. You can distinguish a local minimum from a global minimum by comparing the potential energy (i.e. y coordinate) at each minimum. The one with the lowest
potential energy is the global minimum.
Really great explanation. Rk2918 (talk) 13:31, 20 May 2019 (BST)
Question Two
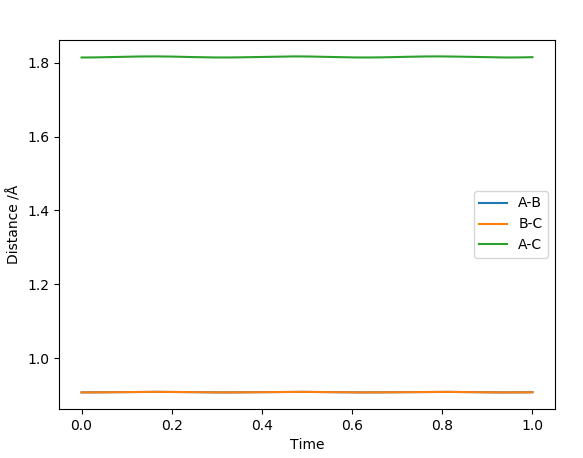
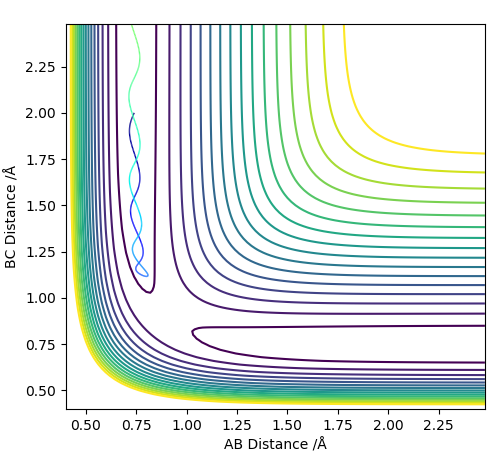
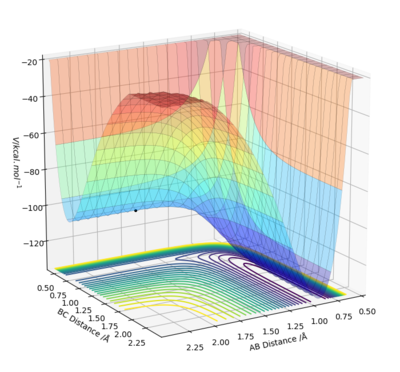
Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” plot for a relevant trajectory.
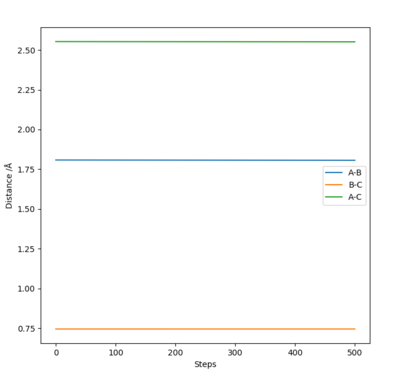
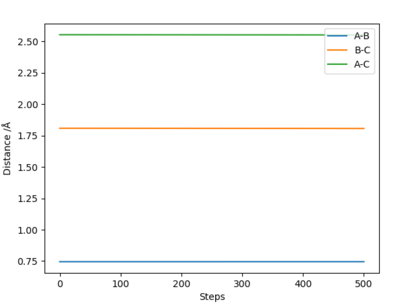
Best estimate of transition state is at A-B distance= B-C distance= 0.907 Å
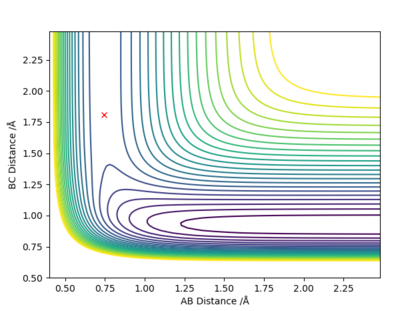
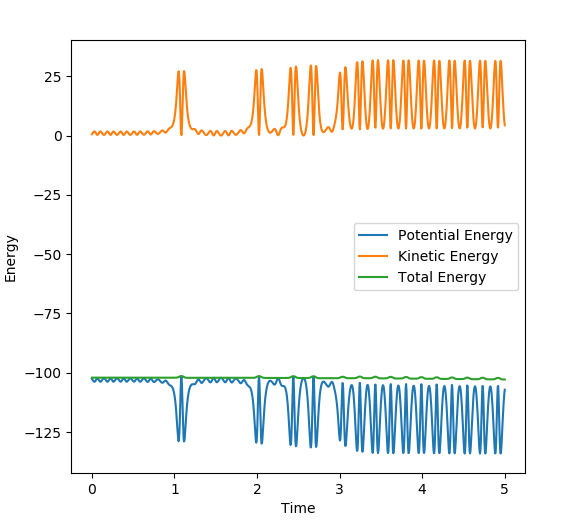
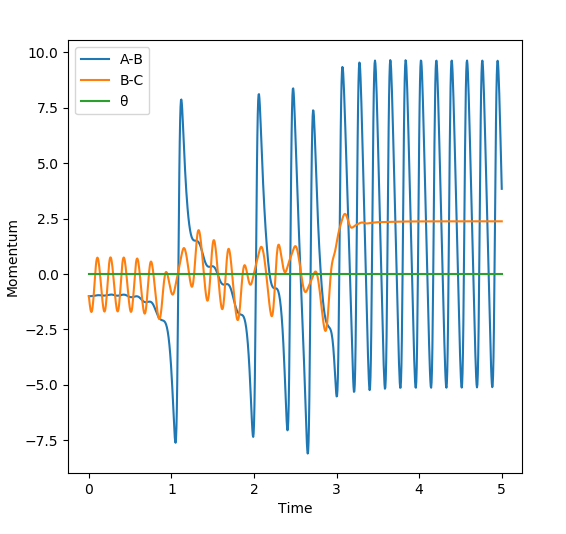
This was estimated using Hammond's postulate and trial and error dynamics analysis. Hammond's postulate states that the structure of a transition state will resemble either the reactants or products more depending on what the transition state is closer in energy too. In this case, the the reaction is very symmetrical. The reactants are the same as the products and so have the same energy level as the products. Therefore the transition state is exactly in the middle of the 'two' structures, half way between the reactants and products (due to symmetry of the reaction and Hammond's postulate). This means that the three atoms involved will all be the same distance apart at the transition state. I.e. A-B= B-C (See diagram) Therefore, trials were carried out using equal distances for AB and BC. The best estimate for the transition state was the bond distance where the molecule oscillated the least (i.e most flat line inter nuclear distance vs time plot).
This diagram was calculated through trial and error using dynamics method and so the line isnt perfectly flat as using a dynamics method means you can get to the exact exact transition point, just very very close to it.
Question Three
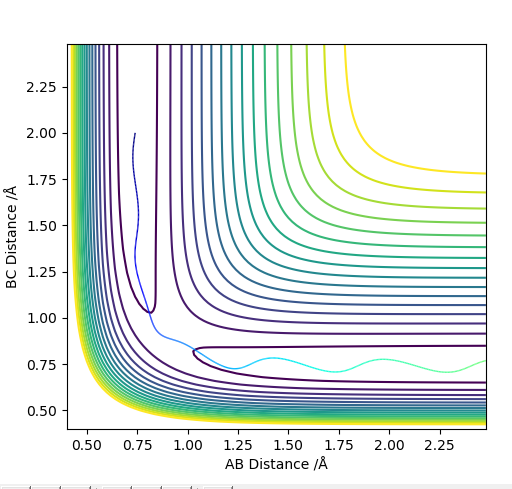
Comment on how the MEP and the trajectory you just calculated differ.
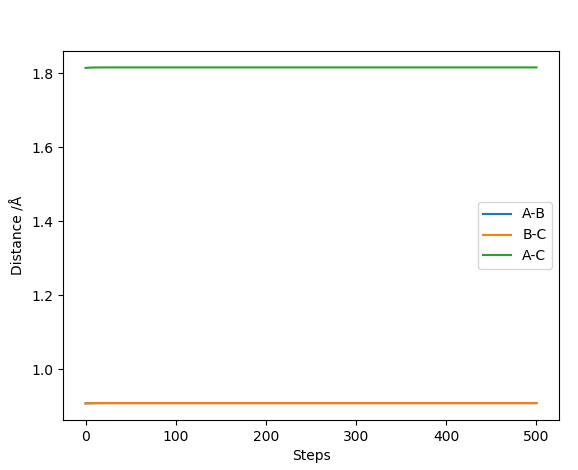
The dynamics analysis method carries over momentum from the previous result so even with the gradient reaches zero, it moves past that point meaning the line doesn't stop at the transition point and the Could do trial and error but this will take a long time- this is because Dynamics analysis carries over the momentum from the previous iteration so even if the gradient gets to zero, it will move past that and the line wont stop at the transition point. It will oscillate around that point. This is why the graph of inter nuclear distance vs time (using trial and error and dynamics analysis) is still is not completely flat.
MEP fixes this problem, minimum energy pathway, momentum and velocities are reset for each infinitesimally small step. Therefore when the gradient hits zero it will stay at this point which is the transition state saddle point. This is a more accurate and easier way to find the saddle point than using the dynamics method.
The calculated MEP distance was found to be 0.907742 Å
MEPs show a minimum energy pathway that a reaction could take which is the minimum energy trajectory along the potential energy surface. Dynamics analysis by contrast shows a reaction trajectory for the entered parameters.
Question Four
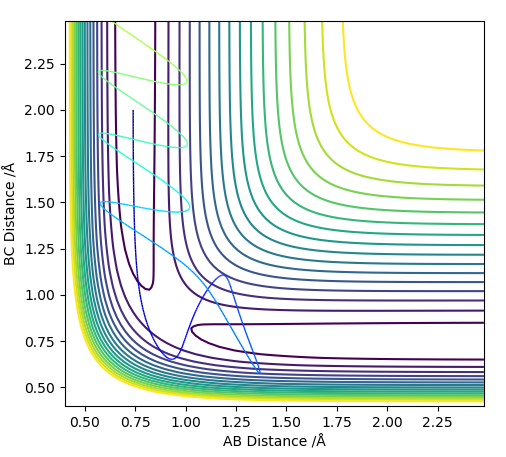
Complete the table above by adding the total energy, whether the trajectory is reactive or unreactive, and provide a plot of the trajectory and a small description for what happens along the trajectory. What can you conclude from the table?
| p1 | p2 | Etot | Reactive? | Description of the dynamics | Contour Plot | |
|---|---|---|---|---|---|---|
| -1.25 | -2.5 | -99 | Yes | AB collides slowly and smoothly with C, BC move away together | 
| |
| -1.5 | -2.0 | -100 | No | Slow moving, slightly toward each other, bounce of each other unreacted, | 
| |
| -1.5 | -2.5 | -99 | Yes | AB collides with C and reacts resulting in vibrating molecule of BC moving away | 
| |
| -2.5 | -5.0 | -85 | No | AB collides with C. B dissociates from A, bounces of C and reconnects with A to move away as an unreacted oscillating molecule of AB | 
| |
| -2.5 | -5.2 | -83 | Yes | AB collides with C. B bonds to C then bounces of of A then moves away as a vibrating molecule connected to C | 
|
This table shows that just adding more energy to a reaction does not necessarily mean that the molecules will react. The momenta of the particles is important. Similarly, more momentum does not necessarily lead to a reaction as can can be seen from the case with p1= -2.5 and p2= -5.0. This is because the molecules need to have the right amount of energy to react and then move away from each other. If they have too much energy they could just dissociate and bounce off of each other like in p1=-2.4,p2=-5.0. Therefore, not only do the particles need enough energy/momentum to get over the transition state, they can't have too much or they can come back over the transition state to the reactants.
Question Five
State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?
Transition state theory is the idea that there is a type of equilibrium (quasi-equilibrium) between the the reactant and products. This equilibrium is at a saddle point of the potential energy surface and is an activated structure which is the transition state. At this transition state there is an activated complex that is high in energy and converts the reactants to the products (i.e. the reactants have to pass through the transition state to get to the products).
The main assumptions of transition state theory are that quantum tunnelling effects are negligible and the Born-Oppenheimer approximation holds true. Also, it relies on the assumption that the reactants are allowed to thermally equilibrate meaning that their energies are Boltzmann distributed and that the reactants are in constant equilibrium with the transition state.
You are just touching on the important point of this answer but not quite there! Think about the idea of barrier recrossing and how TST treats this, and whether it is allowed in real reactions. And now think about how that might affect predictions of reaction rates. Rk2918 (talk) 13:44, 20 May 2019 (BST)
Exercise Two
Question One
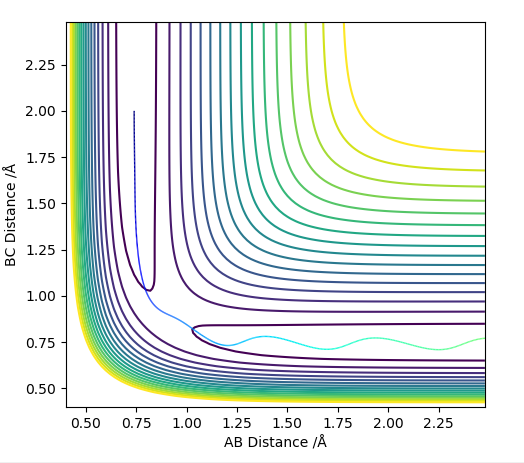
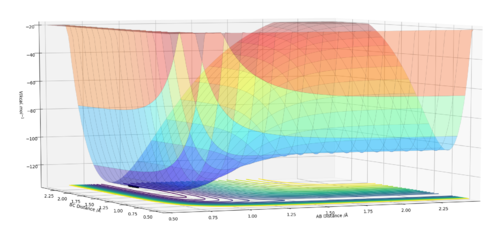
By inspecting the potential energy surfaces, classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?
H2 + F --> HF + H
This is an exothermic reaction as can be seen from the surface plot. (See image where A=F, B=H, C=H). This is in agreement with the theory and relative bond strengths as H-F (565 kJ/mol)1 is a much stronger bond than H2 (432 kJ/mol)1
Hammond's postulate states that a transition state will resemble the reactants or products depending on the activated complex's (transition state's) relative energy compared to the reactants or products. As this reaction is exothermic, the transition state will be early and so nearer the reactants in the potential energy surface.
HF + H --> H2 + F
This is an endothermic reaction, as the potential energy surface plot shows that the reactants are lower in energy than the products.
Using Hammond's postulate, it can be assumed that the transition state (activated complex) is closer in energy to the products than the reactants as endothermic reactions tend to have late transition states.
Question Two: Approximate Transition States
The approximate transition state position for the reaction For H2 + F --> HF + H was found to be when HF distance (AB)= 1.808 Å and HH distance (BC)= 0.745.
The approximate transition state position for the reaction for HF + H -->H2 + F was also found to be 1.808 Å for HF and 0.754 Å for the HH distance. A=H, B=H, C=F
Question Three:Activation Energies
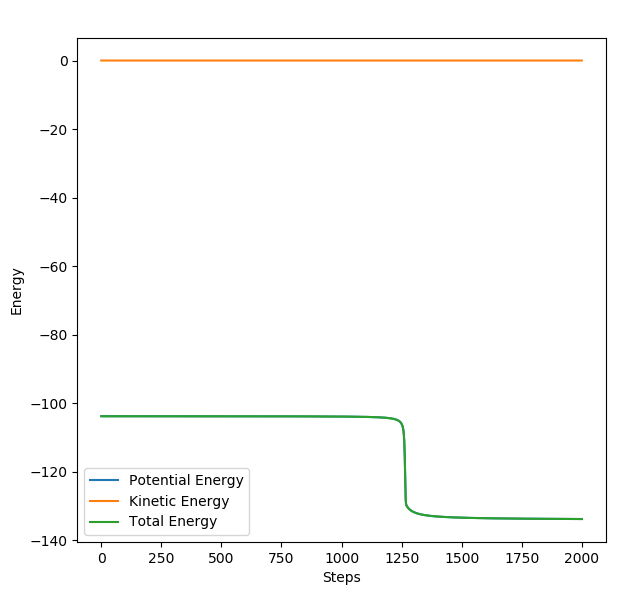
EXOTHERMIC REACTION: H2 + F--> HF + H Once the transition state was found, the MEP paramaters were displaced slightly from these values so that the minimum energy pathway falls back to the reactants level (very small drop). The energy time graph was then analysed to see the energy difference which is the activation energy.
Energy at transition state: -103.8 kcal
Energy of reactants: -103.9 kcal
Activation energy= -103.75--103.90= 0.15 kcal
How did you obtain this energy of reactants value? Maybe here it would be good to include an ultra-zoomed version of this plot to show that it is not a flat line, or to say this in a brief description. Rk2918 (talk) 13:46, 20 May 2019 (BST)
ENDOTHERMIC REACTION: HF + H--> H2 + F
Transition state found, MEP parameters displaced slightly towards the reactants side from saddle point so that the minimum energy pathway 'rolls' back to the reactants side. The energy vs time graph was then analysed to find the activation energy.
Energy at transition state= -103.8 kcal
Energy of Reactants= -133.8 kcal
Activation Energy= -103.78--133.85 = 30.07 kcal = 30.1 kcal (1 dp)
Question Four: Release of Reaction Energy
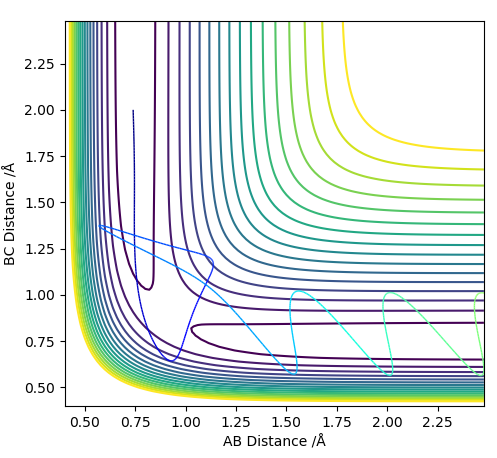
A reactive trajectory was found for the reaction of H2 and F with initial parameters:
HF distance= 1.5 Å, HH distance= 0.8 Å, HF momentum= -1.5 HH momentum= -1.5 giving the following energy vs momentum graph. The diagram shows that the H2atom approaches the F atom, bounces off of it twice and then joins with the F to make HF.
As this reaction is an exothermic reaction energy is released to the surroundings. Overall energy is conserved as the change in potential energy from the reaction is converted to kinetic energy of the molecules in the form of vibrational and translational energy. The release of potential energy as kinetic energy could also be measured experimentally using calorimetry tests.
What is a calorimetry test? How does it work and why does this mean it could be used to probe this? Rk2918 (talk) 13:47, 20 May 2019 (BST)
Question Five: Trends with Momentum
This section investigates the effect of varying the translational and vibrational energy of the reactants on the likelihood of a reaction occuring.
EXPERIMENT ONE: FORWARD EXOTHERMIC REACTION- H2 +F--> HF + H
The reaction of H2 + F --> HF + F was analysed with initial conditions HH distance = 0.74 Å, HF distance = 2.0 Å and momentum of FH= -0.5
This tests the effect of changing the vibrational energy of the reactants on the likelihood of a reaction occuring.
| p(HF) | Reactive? |
|---|---|
| -3.0 | Yes |
| -2.5 | Yes |
| -2.0 | Yes |
| -1.5 | No |
| -1.0 | Yes |
| -0.5 | Yes |
| -0 | Yes |
| 0.5 | Yes |
| 1.0 | No |
| 1.5 | Yes |
| 2.0 | Yes |
| 2.5 | No |
| 3.0 | Yes |
These results don't show a clear trend. This implies that the vibration energy doesn't have a very significant effect on this specific reaction. This can be explained by the exothermic nature of the reaction and Polanyi Rules which are explained below.
The effect of translational energy on the likelihood of a reaction occuring by varying the HF momentum very slightly from -0.5 to -0.8. The energy vs momentum graphs for both situations are shown and compared below to analyse the effect of varying translational energy. (Other initial conditions: HH momentum= -1.5, HF distance= 2.0, HH distance= 0.74)
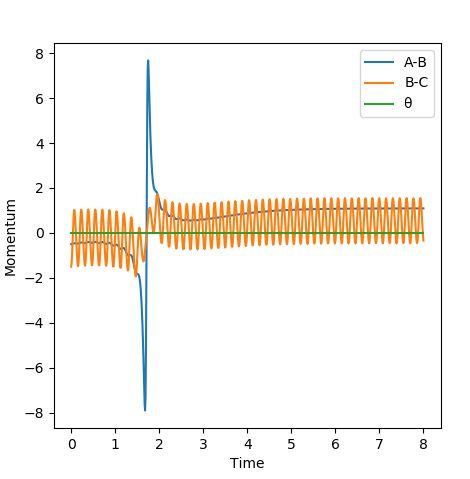
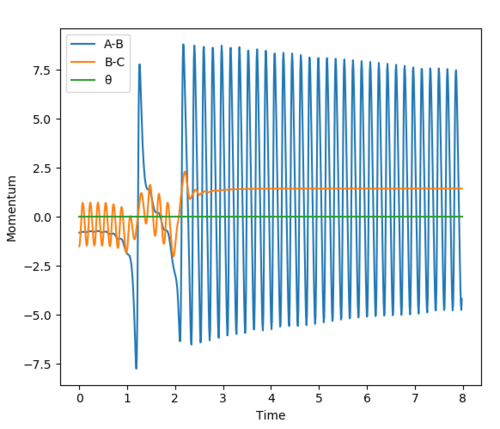
Figures A and B show that a small difference in translational energy significantly increases the likelihood of a reaction occuring. This can be explained by Polanyi Rules (explained below in section 'Question Six').
EXPERIMENT TWO: ENDOTHERMIC REACTION- HF + H--> H2 + F
The endothermic reaction reaction of HF + H --> H2 + F was carried out with initial conditions of HF distance= 0.91 Å, HH distance= 2.0, HF momentum (represents vibrational energy)= 5.0
| p(HH) (represents translational energy) | Reactive? |
|---|---|
| -5.0 | Yes |
| -4.0 | No |
| -3.0 | No |
| -2.0 | No |
| -1.0 | No |
This shows that you need a very large translational energy to cause a significant change whereas when experimenting with the vibrational energy of the HF molecule it was found that a small change in vibrational energy had a larger effect. This is in line with theoretical expectations outlined by Palonyi's Rules.
Question Six: Polanyi's Rules
Reactants need a certain amount of energy (the activation energy) in order to react when they collide. This energy can be in the form of translational and vibrational energy. The way that the energy is distributed between the two forms and the amount of each form of energy effects the likelihood of a reaction happening when they collide. The amount to which the probability of the reaction occuring varies with changes in the translational and vibrational energy depends on what type of reaction it is and the position of the transition state.
Polyani's Rules state that for a reaction with an early transition state (exothermic), the translational energy has the most significant effect on the probability of the reaction occuring. For a reaction with an early transition state, a greater amount of translational energy will increase the proabability of a reaction happening2. Whereas, an increase in vibration energy will have a much less significant effect.
The rules also state that the reverse is true- for a reaction with an late transition state (endothermic), the vibrational energy has the most significiant effect on the probability of the reaction occuring while the translational energy has less of an effect.
FORWARD EXOTHERMIC REACTION: H2+ F--> HF + H
The polyani rules theory supports the above experimental results (Fig. A and B) which shows that, for an exthothermic reaction (early transition state), a small change in translational energy (HF momentum) results in a reaction going from not reacting to reacting. (See Figs A vs B). It also supports the experiment (See table in Question Five section) which shows that changes in vibrational energy don't have a significant effect/clear trend effect on the probability of a reaction occuring.
REVERSE ENDOTHERMIC REACTION: HF + H --> H2 + F
The experiment agrees with the theory states in polyani's rules as it shows that a small change in vibrational energy will result in a reaction occuring that previously didnt whereas changes in translational energy are less effective in changing whether a reaction will occur or not.
Every one of your answers is very detailed and thorough and you have demonstrated very well that you have a deep understanding of this investigation. Other than the few areas where I have made specific comments this is all really great. Rk2918 (talk) 13:52, 20 May 2019 (BST)
References
1. Yoder, C. (2019). Common Bond Energies (D. [online] Wiredchemist.com. Available at: http://www.wiredchemist.com/chemistry/data/bond_energies_lengths.html [Accessed 10 May 2019].
2. Brouard.chem.ox.ac.uk. (2019). Controlling Reagents and Characterising Products. [online] Available at: http://brouard.chem.ox.ac.uk/teaching/dynlectures4to6.pdf [Accessed 10 May 2019].