MDR:AGATHE'S REPORT
MOLECULAR REACTION DYNAMIC LAB REPORT
Important general comment: there are no references! You should get in the habit of providing those in every piece of assignment you deliver. Especially as in, e.g., your final thesis, missing references can be considered plagiarism. ) Fdp18 (talk) 13:20, 9 May 2020 (BST)
Please make use of the wiki built-in reference tool. [1] Fdp18 (talk) 14:58, 9 May 2020 (BST)
EXERCICE 1- H + H2 system
This section will describe the dynamics of a H1 + H2-H3 system. The objectives are to form a new H1-H2 bond. In this exercise, the three atoms considered will be H1, H2 and H3 and are respectively referred to A, B and C.
QUESTION 1: On a potential energy surface diagram, how is the transition state mathematically defined? How can the transition state be identified, and how can it be distinguished from a local minimum of the potential energy surface?
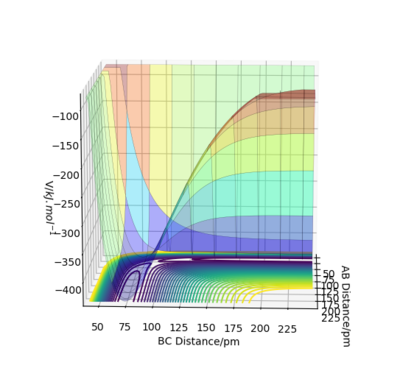
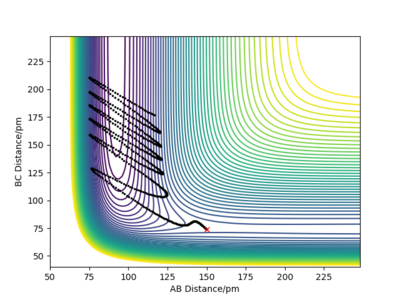
In Figure 1, you are also showing the potential energy as a function of the bond distances. It is just a different way of plotting it - instead of the 3D surface, Figure 1 is the 2D projection, i.e. a contour plot. Fdp18 (talk) 11:19, 9 May 2020 (BST)
Mathematically, the transition state can be defined as the point where the first derivative of the potential energy as a function of position is equal to zero, i.e. ∂V/∂r1 = ∂V/∂r2 = 0
The energy minimum corresponds to stable species and saddle points correspond to transition states: the highest energy point on the reaction coordinate. This corresponds to the lowest energy pathway connecting a chemical reactant to a chemical product.
* Fdp18 (talk) 11:27, 9 May 2020 (BST)
The transition state is thus a maximum and can be recognised from a local minimum, which corresponds to the points where the chemical species is stable. Indeed, the transition state is a form in an inert state, where a particle cannot obtain any momentum if it has no momentum at this point.
* The first part is ok, but here it gets confusing. While minima, maxima, and saddle points indeed are stationary points (i.e. the first derivatives are zero), they differ in their second derivatives. A 'Transition State' is a saddle point (more accurately, a saddle point of first order). Only in one dimension is it a 'maximum'. Maybe take a look at the first year comp lab Fdp18 (talk) 11:27, 9 May 2020 (BST)
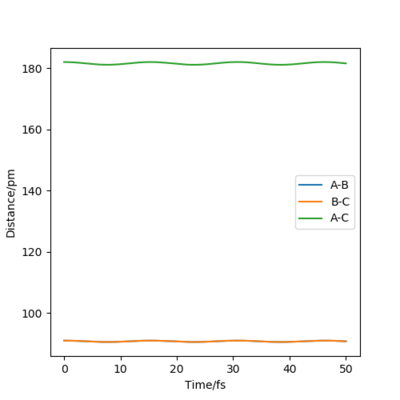
QUESTION 2: Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” plot for a relevant trajectory.
The transition state position is attained when rAB = rBC = 91 pm as at these distances the atoms don't oscillate to a great extent and the internuclear distances do not vary greatly with time. The picture below shows that the intermolecular distances vary a minimum as a function of time, as in the transition of this reaction, the middle H atom forms bonds with both atoms, thus the transition state has less rotational freedom and the vibrations are therefore less important. Moreover, from the plot showing the internuclear distances with time, it is observed that no reaction in going on as the distances between the atoms are almost constant. The plot confirms that the transition state is attained as the H-H-H system has no momentum.
I don't understand what you mean by 'rotational freedom - we only look at the two bond distances, so rotations are not relevant. How could you obtain a better estimate of the transition state? Tip: make the bonds a bit longer (but still the same!) and then start the dynamics run again. Fdp18 (talk) 11:36, 9 May 2020 (BST)
As shown on the animation picture above, the molecules in the transition state do not vibrate a lot as they are locked in a specific configuration as the the central atom is breaking its H-H bond with one H atom and forming a bond with another H atom. Thus there are less degrees of freedom, restricting the bond vibration.
This last part is not entirely correct, maybe because of wording. I agree that the term 'degree of freedom' can be interpreted in different ways, which means that you have to be precise in what you mean here. Furthermore, 'bonds' are not well defined either - we know what they are and that they 'exist', but there are cases (very long bonds, very weak bonds, bonds over more than one centre) that challenge our definitions. This is such a case. Fdp18 (talk) 11:36, 9 May 2020 (BST)
QUESTION 3: Comment on how the mep and the trajectory you just calculated differ.
The reaction path is the minimum energy path (MEP) and is the quickest path a reaction can take. In this simulation, the momenta are defined to equal 0 g.mol-1.pm.fs-1. This results in motions that are completely driven by Coulombic interactions (attractive forces) . After traveling a defined distance, the atoms attain a stable state and do not shift further away, unlike in classical dynamics theory.
The 'MEP' is not the fastest path a reaction can take, since it is not a path that the atoms would naturally take at all. Try to be more precise with wording here. The same applies to 'entirely defined driven by Coulombic interactions': You are right in the sense that out of the four fundamental forces, only electrostatic interactions significantly contribute to the potential we are working in here. However, in Molecular Dynamics, the term 'Coulombic interactions' is used only for the electrostatic interaction between atomic point charges, so you need to be precise for me to see that you understand it. The point is that all those underlying physics (including concepts like pauli repulsion) are combined in the model potential we allow the atoms to move in. Fdp18 (talk) 12:58, 9 May 2020 (BST)
Please refer to the above comment I made in another report earlier today. Are 'quickest path' and 'completely driven by Coulombic interactions' mentioned in some part of the experiment that I missed? If yes, please let me know. Fdp18 (talk) 12:58, 9 May 2020 (BST)
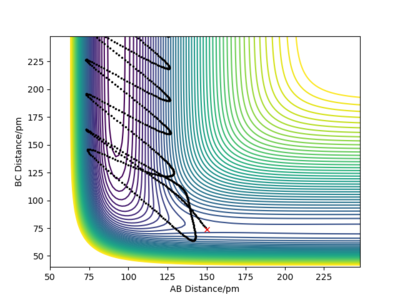
When the distance from the transition state position is changed, the mep also changes. The mep was found to be linear and vibrations were not present. This is a different calculation type, thus the dynamics have disappeared. The trajectory shown for the dynamics occurs with vibrations, shown by the variation in the distances. The MEP removes these vibrations and thus it takes more steps for the reaction to go to completion. Moreover, the MEP shows that the trajectory stops at 200 pm, however the dynamics shows that the trajectory doesn't stop because of the conversation of momenta.
The graphs show contour plots of the potential energy surface for the system close to the transition state where rAB = 92 pm, rBC = 91 pm. The trajectory indicates the molecule travels continuously in the dynamics case or until it uses all the available electrostatic potential energy.
As r(AB) > r(BC)= r(TS), the system returns to its initial form of H1 + H2-H3. However, when rAB = 91 pm, rBC = 92 pm, the system will more likely find itself in another configuration : H1-H2 + H3. Both systems have the same energy, as they have the same variations of internuclear distances variations as a function of time.
As before, 'electrostatic potential energy' is infelicitous wording. It is technically correct, but also obstructs a large part of the physics. Fdp18 (talk) 13:01, 9 May 2020 (BST)
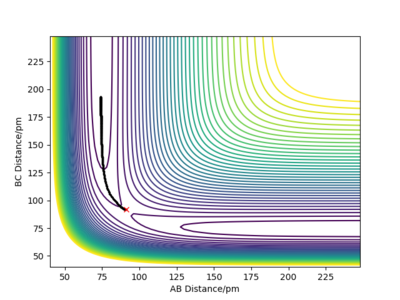
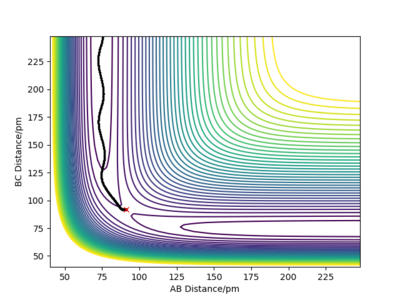
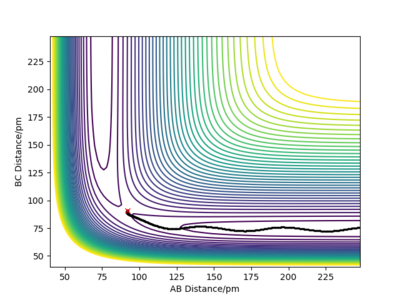
Look at the “Internuclear Distances vs Time” and “Momenta vs Time”. What would change if we used the initial conditions r1 = rts and r2 = rts+1 pm instead?
When observing the two types of graphs ( “Internuclear Distances vs Time” and “Momenta vs Time”), we can conclude that the reverse process is occurring. Indeed, when r1=91 pm, the transition state forms molecule BC. As the BC (r1) bond length is shorter. Atom C thus attracts atom B as they are closer to each other and the attractive force is greater. Note that, albeit the attractive forces will be greater the closer atoms get, the interactions at short range are dominated by repulsive forces beyond a point. Fdp18 (talk) 13:05, 9 May 2020 (BST)
However, when r1=92, the BC bond length is longer than the AB=r2 bond length, so the B and C atoms are further apart thus molecule AB is formed.
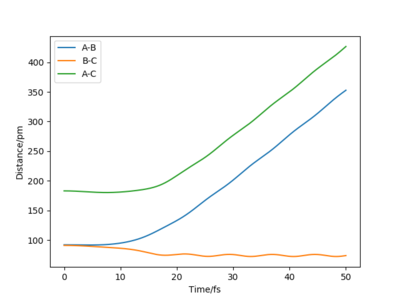
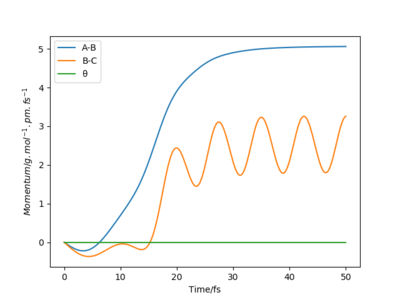
Moreover the trajectory differs, as δ is increased to δ=9 pm, the vibrations become more intense as the molecule being reacted has more distance to go through. When r1=100 pm the distance between the reactants B and C is larger, therefore the attraction between the two atoms is less important. The r2=91 pm, the distance between A and B is thus short and the attractive force between AB is greater so AB forms. When r1=92 pm, the distance between B and C is still grater than between A and B, therefore the formation of the AB molecule is still more favourable. However, it takes more time for the AB molecule to form as the r1 and the r2 distances are similar. Both A and C attract B almost equally as the distances are similar.
QUESTION 4: Setup a calculation where the initial positions correspond to the final positions of the trajectory you calculated above, the same final momenta values but with their signs reversed.What do you observe?
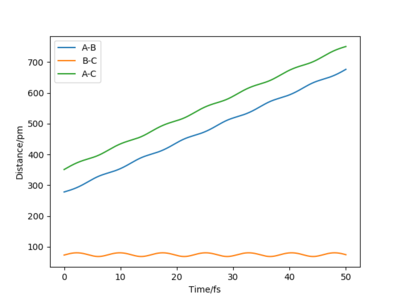
By reversing the signs of the momenta, it is observed that for the positive values of momenta, the pathways of both of the reactants will never meet as they will move further apart from each other. However, when the momentum is negative, the pathways of the reactants will meet as the reactants will move closer to each other.
QUESTION 5: Complete the table above by adding the total energy, whether the trajectory is reactive or unreactive, and provide a plot of the trajectory and a small description for what happens along the trajectory. What can you conclude from the table?
The table below shows examples of atoms at rAB = 230 pm and rBC=74 pm, having different momenta and therefore different reactivities.
Table illustrating the reactive and unreactive trajectories of the H-H-H system for different values of momenta
| p1/ g.mol-1.pm.fs-1 | p2/ g.mol-1.pm.fs-1 | Etot (kJ.mol-1) | Reactive? | Description of the dynamics | Illustration of the trajectory |
|---|---|---|---|---|---|
| -2.56 | -5.1 | -414.28 | yes | Small oscillations. C approaches AB, bonds to B as A move further away. The new molecule BC is oscillating and distances itself from A.The reactants have sufficient energy to overcome the transition state and therefore when the two reactants collide the product is formed. |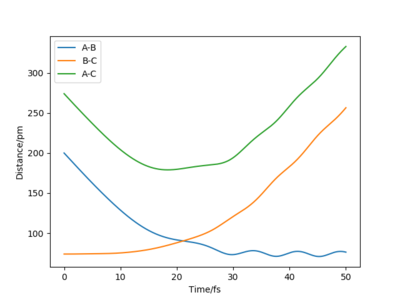  
|
| -3.1 | -4.1 | -420.07 | no | Very small oscillations for the A-B molecule. rBC decreases, then increases with no collision between the atoms. Not enough energy to overcome the activation barrier so the molecules do not react. The trajectory shows that the reactants are colliding but there is not enough energy to overcome the transition state, therefore the trajectory turns round and returns to the reactants. |  
|
| -3.1 | -5.1 | -413.78 | yes | Small oscillations again. C approaches the molecule and collides with A-B and A moves away. The new molecules oscillates and moves further apart from A. The reactants are sent consider rephrasing - this surface describes all possible combinations of these three atoms (as long as they're linear), it's not like we push them in a physical valley. Fdp18 (talk) 13:11, 9 May 2020 (BST)
onto the surface with a high relative velocity. They have sufficient energy to overcome the activation barrier, and at small distances they eventually build up the repulsive forces on the surface, before rolling back down again and following an oscillating trajectory out into the product channel. || | |
| -5.1 | -10.1 | -357.28 | no | Significant oscillations. C approaches the A-B molecule and forms a bond with B. A moves away slightly then returns to its initial position to reform a bond with B. As a consequence, C pulls away. The reactants have a reasonably high relative velocity, but the position of the barrier in the exit channel for the reverse reaction. There is sufficient energy to overcome the activation energy, therefore the product formed dissociates back into the reactant. |  
|
| -5.1 | -10.6 | -349.48 | yes | Important oscillations. C approaches the A-B molecule and collides with it to form a bond with B. A pulls away then moves closer to B to form the transition state again. It then moves further apart as the new molecule B-C oscillates. There is sufficient energy to overcome the activation energy barrier, therefore the reactants collide to form the product. |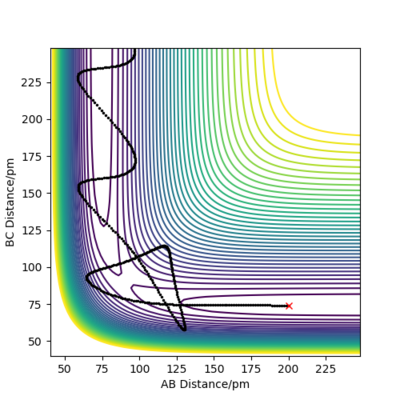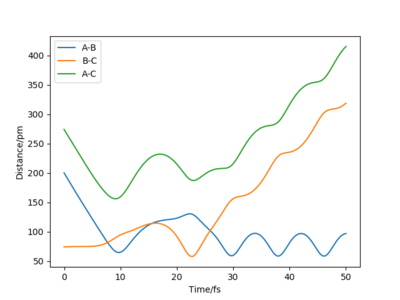  
|
From this table, we can conclude that sufficient energy is needed to overcome the transition state, otherwise a trajectory similar to the second trajectory in the table would occur, where the system has not enough energy to overcome the transition state. However, if there is too much energy in the system then the product formed will dissociate back to the reactants, as it did in trajectory 4.
QUESTION 6: Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?
The transition state theory predictions will deviate from the experimental values as the theory assumes the reaction system will pass over the lowest energy saddle point on the potential energy surface, to react. Indeed, molecules populate higher energy vibrational modes and their motion becomes more complex and collisions may lead to transition states far away from the lowest energy saddle point. Moreover, the transition state theory assumes that unless atoms or molecules collide with enough energy to form the transition structure, then the reaction does not occur. For any barrier with a finite amount of energy, there is a possibility that particles can still tunnel across the barrier.
the strict definition of a transition state is so that there is just one. You use a more casual definition here. That is ok, but you should add a few sentences to explain precisely what you're talking about. Fdp18 (talk) 13:15, 9 May 2020 (BST)
I'm missing a clear presentation of the assumptions of TST, as well as a reference. Fdp18 (talk) 13:15, 9 May 2020 (BST)
Last but not least: although inferred from the part before (with the table), you should mention 'barrier recrossing' again here, as well as its effect on the reaction rates compared to TST. Fdp18 (talk) 13:17, 9 May 2020 (BST)
EXERCICE 2: F - H - H system
In this section, the dynamics of the F-H-H system are studied. The different atoms F, H1 and H2 will respectively be referred to as A, B and C.
QUESTION 1: By inspecting the potential energy surfaces, classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved? Locate the approximate position of the transition state.
The F + H2 reaction is exothermic and the H + HF reaction is endothermic. In exothermic reactions, more energy is released when the bonds are formed in the products than is used to break the bonds in the reactants. Exothermic reactions are characterised by an increase in temperature of the reaction mixture. Chemical reactions that absorb energy overall are endothermic. Therefore the H-F bonds are stronger than the H-H bonds as the energy used when breaking H-F is larger than the energy released in the formation of H-H. This conclude is supported with the fact that the H-F bond is strengthened by the dipole moment due to the fluoride, therefore requiring more energy to break, so a higher dissociation energy.
Not sure what the dipole moment has to do with this. Consider N2, which has no dipole moment. What is more reactive? Fdp18 (talk) 13:24, 9 May 2020 (BST)
The transition state was found to be at 182 pm for the H-F bond and 74 pm for the H-H bond: this corresponds to the position where the bond vibrations are minimised as the central H atom forms a bond with both the other H atom and the F atom.
From Hammond's postulate, the transition state for F + H2 is early as the reaction is exothermic, thus the transition state will ressemble the reactant, i.e. H2
However, for H + HF, the reaction is endothermic so a late transition state is observed, therefore the transition state will resemble the product, i.e. H2
On the potential energy surface plot, it can be observed that the reaction pathway that forms the product H-F is lower than the the reaction pathway that gives the product H2. Thus, this confirms that H-F + H is exothermic, whilst the formation of H-H + F is endothermic.
QUESTION 2: Report the activation energy for both reactions.
how did you obtain these?Fdp18 (talk) 13:28, 9 May 2020 (BST)
The energies of each state are : E(H-F) = -560.70 kJ.mol-1; E(H-H) = -434.183 kJ.mol-1; E(TS)= -433.70 kJ.mol-1.
The activation energy for the H + HF reaction is 127 kJ. mol-1, as the energy required to move to the products is greater as the reactants are more stable than the products. The activation energy for the F + H2 reaction is approximately 1.13 kJ.mol-1. Here, the energy required is lower as the reactants are higher in energy than the products.
QUESTION 3: In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. Explain how this could be confirmed experimentally.
The conditions required for H2+F to be reactive are rH-H=74pm, p(H-H)= 3 g.mol-1. pm. fs-1 and rH-F= 135 pm and p(F-H)=-4 g.mol-1. pm. fs-1.
The transition state for H2+F is early as the reaction is exothermic therefore according to Polanyi’s rules, there is an attractive release of energy. The barrier occurs in the entrance channel. Exothermicity is released before H-F reaches equilibrium position. There is thus a preferential release of exothermicity into product vibration.
A few remarks on this sentence.
- It is hard to understand, I recommend reading your sentences again after a while - sometimes that's enough to spot difficulties.
- Furthermore, you have not stated what Polanyi's rules are (or I have missed it. There are also no references at all).
- What do you mean by 'attractive release of energy'?
- 'Exothermicity is released' should rather be something like 'The energy liberated by the exothermic reaction is released into...' Fdp18 (talk) 13:35, 9 May 2020 (BST)
QUESTION 4: Setup a calculation starting on the side of the reactants of F + H2, at the bottom of the well rHH = 74 pm, with a momentum pFH = -1.0 g.mol-1.pm.fs-1, and explore several values of pHH in the range -6.1 to 6.1 g.mol-1.pm.fs-1 (explore values also close to these limits). What do you observe?
When r(H-H)= 74= r1 pm and r(F-H)=150 pm=r2:
| p1/ g.mol-1.pm.fs-1 | p2/ g.mol-1.pm.fs-1 | observations | Figure showing the trajectories of the molecule |
|---|---|---|---|
| -6.1 | -1.0 | The system has a lot of energy therefore the H2 molecule reacts with F to form the H-F molecule. But as the molecule has more energy that the activation energy barrier the HF molecule reacts with H and overcomes the activation energy to go back to the reactants and an equilibrium between the products and the reactants is established | 
|
| -4.5 | -1.0 | The system has a lot of energy therefore the H2 molecule reacts with F to form the H-F molecule. But as the molecule has more energy that the activation energy barrier the HF molecule reacts with H and overcomes the activation energy to go back to the reactants. | 
|
| -1.0 | -1.0 | Sufficient energy to go through the activation barrier and to form HF. | 
|
| 0 | -1.0 | Sufficient energy to go through the activation barrier and to form HF. | 
|
| 4 | -1.0 | The system has a lot of energy therefore the H2 molecule reacts with F to form the H-F molecule. But as the molecule has more energy that the activation energy barrier the HF molecule reacts with H and overcomes the activation energy to go back to the reactants | . 
|
| 6.1 | -1.0 | The system has a lot of energy therefore the H2 molecule reacts with F to form the H-F molecule. But as the molecule has more energy that the activation energy barrier the HF molecule reacts with H and overcomes the activation energy to go back to the reactants and an equilibrium between the products and the reactants is established | 
|
It is observed that when significant amounts of energy are put into the H-H bond, it dissociates and forms HF. However, when too much energy is contained into the system, this H-F bond just formed, also dissociates to form H2 again. This results in going back to the reactants. In some cases, the energy of the system is larger that the activation energy barrier so it can also overcome the activation energy required for the reverse pathway.
Think about the last sentence: if the systems was able to cross the barrier in the first place, and if energy is conserved, than there is always enough energy to overcome the activation barrier in the other way... Fdp18 (talk) 13:37, 9 May 2020 (BST)
QUESTION 5: For the same initial position, increase slightly the momentum pFH = -1.6 g.mol-1.pm.fs-1, and considerably reduce the overall energy of the system by reducing the momentum pHH = 0.2 g.mol-1.pm.fs-1. What do you observe now?
When the momentum pFH = -1.6 g.mol-1.pm.fs-1, and the overall energy of the system has been reduced by changing the momentum pHH = 0.2 g.mol-1.pm.fs-1, we can observe that the initial reactant H2 tries to approach F, but it doesn't have enough energy to overcome the activation barrier.
I agree that there will not be enough energy to overcome the barrier. However, your trajectory doesn't show that: the reactants have not met yet, so they weren't even given the chance to (not) react. Fdp18 (talk) 13:39, 9 May 2020 (BST)
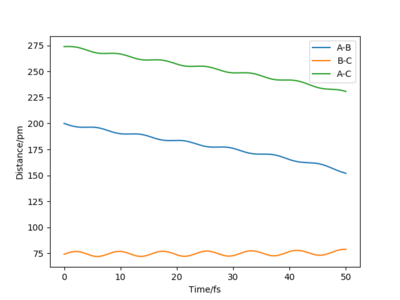
QUESTION 6: Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.
Polanyi's rules predict how the activation barrier location influences the energy requirement in an atom and diatom chemical reaction. For the exothermic H2+F reaction, the reaction barrier is located in the entrance valley of the reaction, thus it is an early barrier. The reactant's translational energy is then more efficient than vibration to overcome the barrier to reaction, thus, accelerating the reaction rate. The available energy will then be transferred to product vibration for the early-barrier reaction.
'entrance valley' is not commonly terminology. That's not a problem per se, but it means that you need to define it here. (or before) Fdp18 (talk) 13:41, 9 May 2020 (BST)
However, for the endothermic reaction HF+H, the reaction is reversed: it is a late transition state. So, a translationally product will be yielded from a late-barrier reaction.
You need to explain more what you mean by 'translational product' - think of a readership who hasn't done this experiment themselves. How would you explain it to them? Fdp18 (talk) 13:43, 9 May 2020 (BST)
Low efficiency reactions have a small cross section, a small probability of head on reactions occurring, and are controlled by short range repulsions. High efficiency reactions have large cross sections, usually react head on and are controlled by long range attraction. Thus, the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction as the cross sections are varied.
Example Reference Section:Fdp18 (talk) 14:58, 9 May 2020 (BST)
<references> [1]