MATLAB nw1315
Molecular Reaction Dynamics
H+ and H2 model
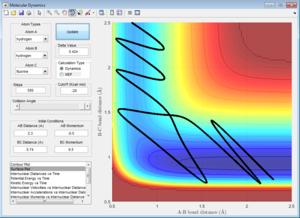
The reactive trajectory of a triatomic collision, in which an atom (A) collides with a diatomic molecule (BC) to produce an alternative diatomic (AB), releasing atom C, can be described by the change of potential energy during the reaction. This can be shown in the H+ and H2 system (Figure 1), where a minimum potential energy pathway is maintained throughout the reaction
(Reference external images. This one shows initial conditions that aren't relevant to what you're saying Tam10 (talk) 10:23, 7 June 2017 (BST))
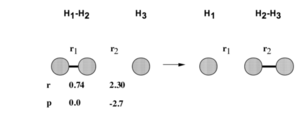
These parameters are used to create a plot of the potential energy of the reaction, with the length of r1 referring to the initial bond length and r2 to the distance between atom A and diatomic BC before the collision. The negative momentum shows a decrease in distance between the atom and diatomic for the initial collision.
The reaction takes place along the 'trough' of the plot, and a transition state occurs at the maximum point of this minimum pathway, where the gradient is equal to zero, with a second differential that is negative as the potential energy will decrease to either the products or reactants, depending on the parameters. A minimum will also have a gradient of zero, however the second differential will give a positive value. Therefore minima and transitions states can be differentiated by the increasing or decreasing of the potential energy of the plot either side of these points.
Determining the Transition State
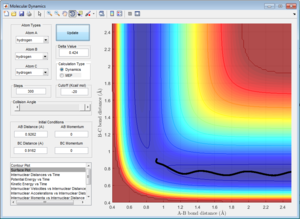
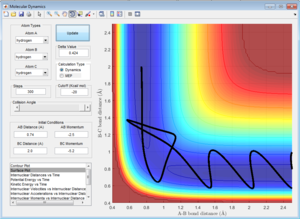
The transitions state should occur when the distance between the atoms is equal, where the bond is both breaking and forming. At data point [0.9176,0.9148,-98.78] (Figure 2), the distances are close to the transitions state, however lie to the side of the maximum of the transition state, so falls to the side of the reactants when put in as the bond lengths with a momentum of zero. These lengths produce the highest potential energy from the parameters set up, as this is the maximum energy the reaction reaches during the transition state.
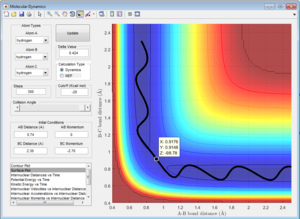
This would suggest that the distance between the atoms during the transition state will be between the coordinates given, possibly a value of 0.9162 Angstroms.
(A method to locate it more precisely was given in the script. Tam10 (talk) 10:23, 7 June 2017 (BST))
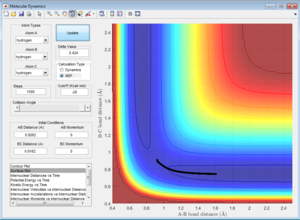
Comparison of MEP and Dynamic Calculations

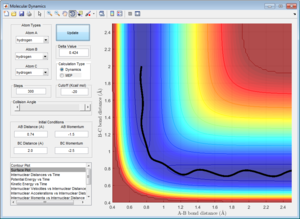
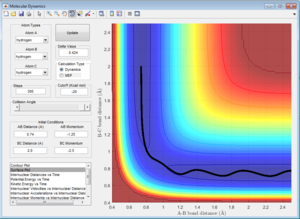
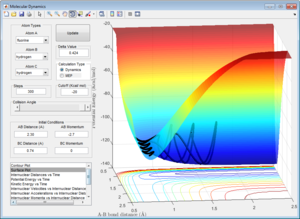
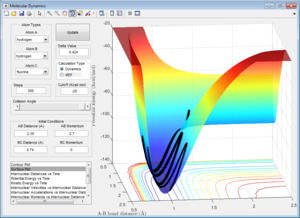
Here the parameters were set to decrease from the transition state maximum, with r1 set to 0.9262 and r2 set to 0.9162 and momentum of zero, allowing the reaction to fall back to the reactants. Although using both the MEP and dynamic calculations show the reaction pathway of the collision, MEP does not take into account the oscillating of the atoms during the reaction (Figure 4), as shown by the smooth line in comparison as to when calculated using dynamic(Figure 5).
| p1 | p2 | Effect on Reaction | Figure Number | |
|---|---|---|---|---|
| 1 | -1.25 | -2.5 | Reactive | 6 |
| 2 | -1.5 | -2.0 | Unreactive | 7 |
| 3 | -1.5 | -2.5 | Reactive | 8 |
| 4 | -2.5 | -5.0 | Reactive | 9 |
| 5 | -2.5 | -5.2 | Reactive | 10 |
(Trajectory 4 is ultimately unreactive. Tam10 (talk) 10:23, 7 June 2017 (BST))

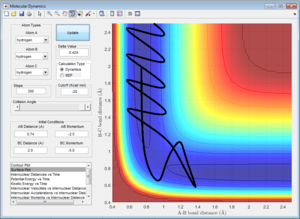
Both 1 and 3 react as seen previously, with the length of the A-B bond lengthening until the B-C bond is formed at the transition state maximum. However in 2 the B-C bond stays intact as the momentum is too low for the A atom to displace it and so is just repelled when it gets too close to the diatomic molecule. In 4 the atom displaces the C atom initially, but the p2 causes the C atom to come back in and collide with the newly formed diatomic, knocking the A atom back out of the diatomic.The momenta are very similar to 4 with 5, but the p2 value is crucially slightly higher, meaning that when the C atom is knocked and oscillates to come back into the diatomic, the diatomic is oscillating so that the A-B bond is long enough to avoid the energy from C breaking the bond, and instead falls away due to it's own momentum.
With 4, transition state theory (TST) applies, where the activated transition state (in this case A--B--C) is able to exist in equilibrium with the reactants (A and B-C), but the transition state must exist long enough for the reaction to fall back to the left. However this theory may fail at higher temperatures where higher vibrational levels are occupied, and the vibration of the complexes formed becomes less predictable, and may form transition states other than the minimum predicted. TST takes into account a classical approach to the reaction, therefore if the incoming atom doesn't have enough energy to get over the activation energy barrier then no reaction will occur. This doesn't take the quantum chemical approach into account, where a degree of tunneling through the activation barrier may occur, and although this may be a negligible amount for high activation barriers, it can contribute substantially with reactions that have lower activation barriers. This may mean that TST predicts a lower rate than will be experimentally seen, as it doesn't take the potential for the reaction to undergo via tunneling as well during the reaction.
F and H2 model
The formation of the FH molecule from the collision between H2 and F is an exothermic reaction, as shown by the decrease in potential energy in the products in comparison to the reactants along the reaction pathway. The new H-F bond formed is therefore stronger than the original H-H bond due to the lower potential energy of the species(Figure 11). Due to this, the inverse reaction from HF and H to H2 and F must be endothermic, which would cause energy needing to be supplied to the system to break the strong dipolar F-H bond and reform a more reactive product(Figure 12).
Determining the Transition State
The transition state lies around [1.56,0.76,-104] for H2 and F, and as the reaction is exothermic, once the bond lengths reach these values, the reaction will spontaneously occur to the products. However with HF and H, the potential energy must reach a value of -104 kcal/mole from -133.8 kcal/mole in order to activate the reaction, showing an activation energy of around 30 kcal/mole needed for the endothermic reaction. In this simulation, the potential energy is not significant for the reaction to go to completion, and so remains as H-F.
| Reaction | A-B/angstoms | B-C/angstroms | Potential Energy/kcal/mole | Reaction type |
|---|---|---|---|---|
| H2 + F | 1.56 | 0.76 | -104 | Exothermic |
| HF + H | 0.76 | 1.56 | -104 | Endothermic |
(This is far off the TS. The gradient must be zero at this point. Tam10 (talk) 10:23, 7 June 2017 (BST))
Experimental Analysis of the Reaction
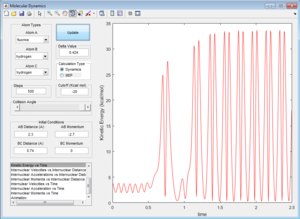
By setting the momentum (p1) to a value of -2.7, the reaction pathway is able to provide enough energy to react, releasing the H atom. Due to the conservation of energy, some is converted to kinetic energy through the increased momentum of the released H atom, while some is converted into vibrational energy within the H-F bond, as shown by the increased vibration of the H-F bond in comparison to the initial H-H bond (Figure 13). This reaction can be monitored via IR spectroscopy of the initial vibrating H-H bonds and the newly formed H-F bonds, with the H-H peaks disappearing as the reaction goes to completion.
Early and Late Transition States
Polanyi's empirical rules state that a late transition state will favour a high vibrational energy and low translational energy while an early transition state will be preferred with high translational energy and low vibrational energy, which can be applied to the endothermic and exothermic reactions respectively. The endothermic reaction between HF and H has a transition state nearer to the products of the reaction, and so by adjusting the amount of vibrational energy put in as shown below, the efficiency of the reaction can be improved. As well as this, the exothermic reaction can be more efficient by increasing the translational energy of the reaction, favouring the early transition state of the reaction.
(You are sometimes using an initial kinetic energy that is far higher than the barrier requires. Tam10 (talk) 10:23, 7 June 2017 (BST))