Lhl17molmod2
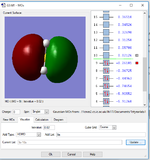
NH3
test molecule |
Optimisation
Molecule name: Ammonia
Calculation method: RB3LYP
Basis set: 6-31G(d,p)
Final energy E(RB3LYP) in atomic units (au): -56.55776873
RMS gradient: 0.00000485
Point group: C3V
Optimised N-H bond distance: B=1.02Å
Optimised H-N-H bond angle A=37°
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES
Vibrational modes
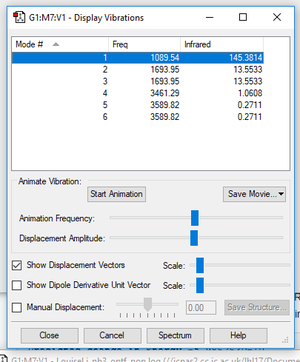
| Vibrational Mode | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Wavenumber/cm-1 | 1090 | 1694 | 1694 | 3461 | 3590 | 3590 |
| Symmetry | A1 | E | E | A1 | E | E |
| Intensity | 145.38 | 13.55 | 13.55 | 1.0608 | 0.2711 | 0.2711 |
Expected number of nodes from 3N-6 rule: 3
Degenerate modes: 2,3 and 5,6
Bending vibrations: 1, 2 and 3
Bond stretch vibrations: 4,5 and 6
Symmetric mode: 1 or 4
Umbrella mode: 1
Number of expected bands in experimental spectrum of gaseous ammonia: 4
NBO charge distribution
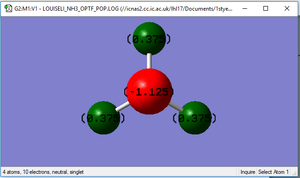
Haber-Bosch calculation
E(NH3)= -56.55776873 au
2*E(NH3)= -113.11553746 au
E(N2)= -109.52412868 au
E(H2)= -1.17853936 au
3*E(H2)= -3.53561808 au
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -113.11553746 - [-109.52412868 + -3.53561808] = -0.0557907 au = -146.4784829 kJ/mol = -146.5 kJ/mol (nearest 0.1 kJ/mol)
N2
test molecule |
Optimisation
Molecule name: Nitrogen
Calculation method: RB3LYP
Basis set: 6-31G(d,p)
Final energy E(RB3LYP) in atomic units (au): -109.52412868
RMS gradient: 0.00000060
Point group: D∞h
Optimised N-N bond distance: B=1.11Å
Item Value Threshold Converged? Maximum Force 0.000001 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES
Vibrational modes
There is 1 vibrational mode at 2457.33cm-1, IR = 0
NBO charge distribution
There is no overall dipole as the molecule is homonuclear.
Mono-metallic TM complex
Unique Identifier: AFUXAD
Bond distance: 1.10550
Equivalent distance in structure: 1.12785, 1.11778
The crystal structure and computational distances are different because in the metal complex, the HOMO-LUMO interactions means electrons are lost from the bonding orbitals of the nitrogen atoms, and gained in the anti-bonding orbitals (the transition metal is taking electron density away from the nitrogen atoms). The bond order is reduced and as a result, the bond length is increased. In addition, the transition metal complex is in a solid state whereas the N2 molecule is gaseous and this also affects bond length.
Furthermore, the RB3LYP calculation method and 6-31G(d,p) basis set used provide only an approximation for the bond length.
H2
test molecule |
Optimisation
Molecule name: Hydrogen
Calculation method: RB3LYP
Basis set: 6-31G(d,p)
Final energy E(RB3LYP) in atomic units (au): -1.17853936
RMS gradient: 0.00000017
Point group: ? D∞h
Optimised H-H bond distance: B=0.74279
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000001 0.001200 YES
Vibrational modes
There is 1 vibrational mode at 4465.68cm-1, IR = 0
NBO charge distribution
There is no overall dipole as the molecule is homonuclear.
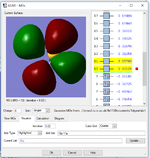
Another small molecule: H2S
test molecule |
Optimisation
Molecule name: Hydrogen Sulfide
Calculation method: RB3LYP
Basis set: 6-31G(d,p)
Final energy E(RB3LYP) in atomic units (au): -399.39162414
RMS gradient: 0.00012068
Point group: C2V
Optimised S-H bond distance: B=1.35Å
Optimised H-S-H bond angle A=44°
Item Value Threshold Converged? Maximum Force 0.000175 0.000450 YES RMS Force 0.000145 0.000300 YES Maximum Displacement 0.000472 0.001800 YES RMS Displacement 0.000386 0.001200 YES
Vibrational Modes
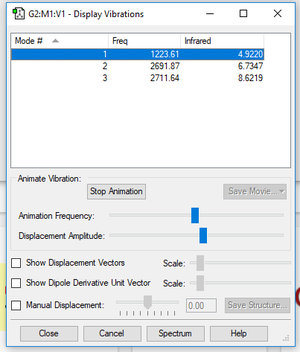
| Vibrational Mode | 1 | 2 | 3 |
|---|---|---|---|
| Wavenumber/cm-1 | 1224 | 2692 | 2712 |
| Symmetry | A1 | A1 | B2 |
| Intensity | 4.922 | 6.7347 | 8.6219 |
| Diagram |  |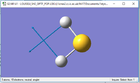
 |
 |
The sulphur atom is more electronegative than the hydrogen atoms and so it has a slight negative charge. The hydrogen atoms have a slight positive charge.
Expected number of nodes from 3N-6 rule: 3
Degenerate modes: None
Bending vibrations: 1
Bond stretch vibrations: 2 and 3
Symmetric mode: 1 and 2
Number of expected bands in experimental spectrum of gaseous H2: 3
NBO charge distribution
Molecular Orbitals
| Molecular orbital diagram | Contributing atomic orbitals | Bonding, antibonding or mixture? | Energy | Occupied or unnocupied? | Effect on bonding |
|---|---|---|---|---|---|
 |
Hydrogen 1s
Sulfur 3p |
Nonbonding | HOMO | Occupied | None (antibonding) |
 |
Hydrogen 1s
Sulfur 3p |
Antibonding | LUMO | Unnocupied | None (antibonding) |
 |
s orbitals of higher n | Antibonding | Very high | Unoccupied | None (antibonding) |
 |
Sulfur 2s | Nonbonding | Low | Occupied | None (nonbonding) |
 |
Sulfur 2p
(1 of 3 degenerate MOs - 2px, 2py, 2pz,) |
Nonbonding | Low | Occupied | None (nonbonding) |
Marking
Note: All grades and comments are provisional and subjecct to change until your grades are officially returned via blackboard. Please do not contact anyone about anything to do with the marking of this lab until you have recieved your grade from blackboard.
Wiki structure and presentation 0.5/1
Is your wiki page clear and easy to follow, with consistent formatting?
YES - However you included the energy calculation of the Haber Bosch process right after the NH3 calculation. At this point you don't have the data on N2 and H2 which are essential for the calculation.
Do you effectively use tables, figures and subheadings to communicate your work?
YES - However all of your jmols are labelled as 'test molecule'. This is not informative at all and should be changed to the name of the molecule or its formula.
NH3 0.5/1
Have you completed the calculation and given a link to the file?
YES
Have you included summary and item tables in your wiki?
YES
Have you included a 3d jmol file or an image of the finished structure?
YES
Have you included the bond lengths and angles asked for?
YES
Have you included the “display vibrations” table?
YES
Have you added a table to your wiki listing the wavenumber and intensity of each vibration?
YES
Did you do the optional extra of adding images of the vibrations?
YES
Have you included answers to the questions about vibrations and charges in the lab script?
YES, however from the 3N-6 rule 6 modes would be expected for a molecule consisting out of 4 atoms. 3*N-6=3*4-6=12-6=6. Additionally, in the experimental spectrum 2 peaks are to be expected and not 4. You correctly identified degenerate modes which lowers the number of modes to 4. Due to their low intensities the stretching modes will not be seen, therefore 2 modes are expected. 0.You did not comment on the calculated charges at all!
N2 and H2 0.5/0.5
Have you completed the calculations and included all relevant information? (summary, item table, structural information, jmol image, vibrations and charges)
YES, you could have explained that the charges are 0 as the electronegativities are equal.
Crystal structure comparison 0/0.5
Have you included a link to a structure from the CCDC that includes a coordinated N2 or H2 molecule?
NO - There is no link or reference given. Therefore, there is no chance to check the given number for the bond length in the crystal structure.
Have you compared your optimised bond distance to the crystal structure bond distance?
YES
Haber-Bosch reaction energy calculation 0.5/1
Have you correctly calculated the energies asked for? ΔE=2*E(NH3)-[E(N2)+3*E(H2)]
YES
Have you reported your answers to the correct number of decimal places?
YES
Do your energies have the correct +/- sign?
YES
Have you answered the question, Identify which is more stable the gaseous reactants or the ammonia product?
NO
Your choice of small molecule 3/5
Have you completed the calculation and included all relevant information?
YES
Have you added information about MOs and charges on atoms?
Your deduction that anti bonding MOs are insignificant for bonding is incorrect! You assigned the HOMO to be built by the as of H and 3p of S. In fact the HOMO resembles just one of the 3p orbitals of S and is nonbonding. You are right that the high energy MO you are displaying seems to be built out of s orbitals of higher n. However you were asked to discuss the MOs you are choosing, therefore you should have constructed the MO diagram to assign the proper s Orbitals which are included.
Independence 0/1
If you have finished everything else and have spare time in the lab you could: Check one of your results against the literature, or Do an extra calculation on another small molecule, or Do some deeper analysis on your results so far
NO - no independent work was identified.