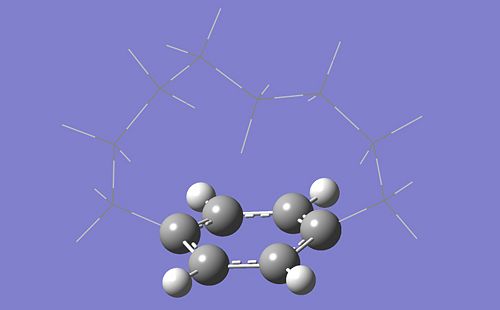
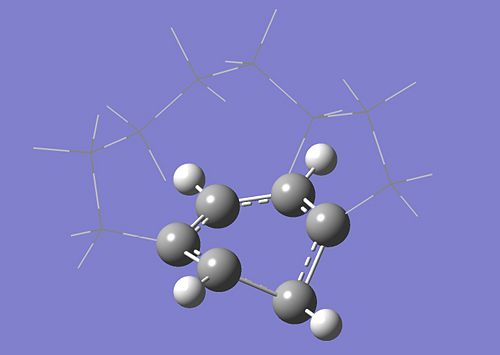
Let's try with a smaller cycle
Introduction
Advice break
First read the parts Introduction, and First steps with ONIOM
Now try to run the same calculations with this new molecule :
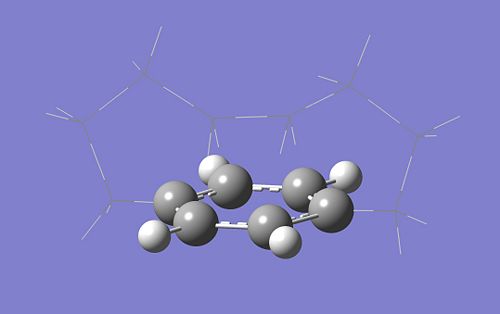
(Benzene and a cycle of 8 carbones)
First, draw the molecule as above, then select the high and low layers as was done in the previous tutorial. The high layer should include the benzene ring, and the environment should be in the low layer. The cycle is smaller and so more stretched. It tends not to be flat. In order to get the right orbitals in the active space (without any mix between sigma and pi orbitals), it's better to force the benzene cycle to be flat during the orbitals section. Then, the geometry should be relaxed.
Note Bene :
All these calculations were run with a development version of Gaussian (gdvh08_806).
Orbitals
Advice break
Before beginning this part make sure that you read the part ONIOM for excited states.
We need initial orbitals for the CASSCF computation. The active orbitals shall be chosen from these molecular orbitals.
Initial orbitals
In order to specify the correct orbitals for the CASSCF active space, they must be calculated them on the high model separately and then read these back into the ONIOM calculation. This is done using the onlyinputfiles option. It is important to use the nosymm keyword in the route section so that the molecular specification is consistent throughout.
#p oniom(hf/sto-3g:am1)=onlyinputfiles pop=full nosymm
The output gives the three parts of the ONIOM calculation as three separate input files. The input file created by the inputfilesonly option, contains a number of ghost atoms. It is not known the exact purpose of these, however, it appears that they act as 'place-holders' for the other atoms in the system that are outside the specific part of the model being calculated. Indeed, if they are not used then, when the orbitals are fed into the full ONIOM calculation, an error message is obtained.
#P Test IOp(2/15=1,5/32=2,5/38=1) RHF/STO-3G
orbitals_flat
Point 2 -- high level on model system.
0 1
C -0.861573850000 -2.705360530000 0.001750920000
C 0.539826080000 -2.705430640000 0.002179930000
C 1.240587010000 -1.491817950000 0.001614740000
C 0.597351930000 -0.167438110000 0.003803130000
C -0.861451930000 -0.278065030000 0.000192820000
C -1.562212860000 -1.491677720000 0.000757740000
H 1.074779510000 -3.632104400000 0.002938500000
H 2.310586960000 -1.491871490000 0.001941870000
H -1.396405360000 0.648608730000 -0.000564350000
H -2.632212810000 -1.491624180000 0.000431570000
H(Iso=12) -1.295943091445 -3.457622827963 0.002100426539
Bq-#1(Iso=1.00782504,Spin=1,GFac=2.792846) -0.883254000000 -4.490611640000 -0.501545890000
Bq-#1(Iso=1.00782504,Spin=1,GFac=2.792846) -2.396418800000 -3.616885180000 -0.502505210000
Bq-#1(Iso=12) -1.719078100000 -4.188834530000 1.454108130000
Bq-#1(Iso=1.00782504,Spin=1,GFac=2.792846) -2.768405890000 -4.397214490000 1.473831030000
Bq-#1(Iso=1.00782504,Spin=1,GFac=2.792846) -1.183313270000 -5.015854910000 1.871113330000
Bq-#1(Iso=12) -1.120889690000 -3.151797470000 2.422779770000
Bq-#1(Iso=1.00782504,Spin=1,GFac=2.792846) -0.295044350000 -3.582882240000 2.949130780000
Bq-#1(Iso=1.00782504,Spin=1,GFac=2.792846) -1.757388370000 -2.640977520000 3.114756950000
Bq-#1(Iso=12) -0.491401960000 -2.062459720000 1.657126450000
Bq-#1(Iso=1.00782504,Spin=1,GFac=2.792846) 0.419228440000 -2.410829260000 1.216341990000
Bq-#1(Iso=1.00782504,Spin=1,GFac=2.792846) -1.182658170000 -1.788160340000 0.887825010000
H(Iso=12) 0.997112155446 0.603454641191 0.025971900794
Bq-#1(Iso=1.00782504,Spin=1,GFac=2.792846) 0.548557320000 1.633329240000 -0.457719050000
Bq-#1(Iso=1.00782504,Spin=1,GFac=2.792846) 2.046840460000 0.736917510000 -0.525984990000
Bq-#1(Iso=12) 1.453825550000 1.276974390000 1.495605940000
Bq-#1(Iso=1.00782504,Spin=1,GFac=2.792846) 2.481559650000 1.366224510000 1.779678200000
Bq-#1(Iso=1.00782504,Spin=1,GFac=2.792846) 0.960159280000 2.214684190000 1.643571970000
Bq-#1(Iso=12) 0.948223970000 0.163648320000 2.431806830000
Bq-#1(Iso=1.00782504,Spin=1,GFac=2.792846) 1.573500390000 -0.585382130000 2.870991040000
Bq-#1(Iso=1.00782504,Spin=1,GFac=2.792846) 0.444210660000 0.706048150000 3.204252960000
Bq-#1(Iso=12) -0.064162800000 -0.720106020000 1.679708890000
Bq-#1(Iso=1.00782504,Spin=1,GFac=2.792846) -0.757957550000 -0.453189660000 0.910095680000
Bq-#1(Iso=1.00782504,Spin=1,GFac=2.792846) 0.810572600000 -1.149794240000 1.238000830000
The high model input can then be used to calculate initial orbitals at the STO-3G level. To do that, you can copy this section in a new input file. The first calculation is carried out on the STO-3G basis set using Hartree-Fock theory and then the size of the basis set is increased to 4-31G.
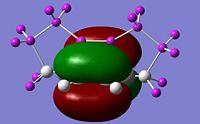
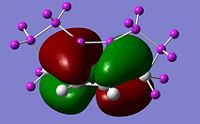
Visualise the orbitals and select the active space
The correct CASSCF active space must be specified in the relevant checkpoint file prior to the ONIOM calculation. This can be done using the orbitals from the RHF/4-31g single point energy calculation. By visualizing the orbitals in GaussView it can be determined that the relevant molecular orbitals are 18, 20, 21, 22, 23, 30. We can use the guess=alter keyword to swap orbitals to run the CASSCF/6-31g* single point energy calculation:
#p cas(6,6)/6-31G(d) pop=full guess=(read,alter) geom=check nosymm orbitals_cas_631gd 0 1 18 19 24 30
|
|
|

|

|

|
Input and output files
Media:orbitals_flat.gjf
Media:orbitals_flat.log
Media:orbitals_flat_hf_sto3g.gjf
Media:orbitals_flat_hf_sto3g.log
Media:orbitals_flat_hf_431g.gjf
Media:orbitals_flat_hf_431g.log
Media:orbitals_cas_631gd.gjf
Media:orbitals_cas_631gd.log
Note Bene :
With the development version of Gaussian (gdvh08_806), the first output file seems to finish with an error. Nevertheless, the job is already done. So we can use the high model section to create the following input file all the same.
Optimise the geometry of the ground state minimum
Now we can read the orbitals and run an optimization of the ground state minimum. As the benzene cycle doesn't need to be flat anymore, the geometry should be relaxed from now. This can be done by "cleaning" it with Gaussview.
Calculation
The energies of the different layers are calculated in the following order:
Low Real
High Model
Low Model
The low model and low real systems have not been calculated yet and so generate must be put so that these are calculated during the oniom calculation. For the high model system, the correctly ordered active space is now held in the checkpoint file of the CASSCF(6,6)/6-31G* single point energy calculation. This must now be read in using the guess=input keyword. We use an IOp(4/69=2) to make sure the orbitals are read from the checkpoint file and are not regenerated again.
#p opt freq oniom(casscf(6,6)/6-31g(d):am1) nosymm guess=input geom=connectivity pop=full IOp(4/69=2) ''Molecular Specification'' generate /work/mvacher/gdv/OniomCI/orbitals_cas_631gd.chk generate
Further information can be found at the bottom of the ONIOM user reference.
Nota Bene
With gdvh01, the syntax is different. There is no extra blank lines.
generate /work/mvacher/gdv/OniomCI/orbitals_cas_631gd.chk generate
Results
The output should indicate that the high model initial orbitals have optimized within a few iterations, indicating that these have been read in correctly from the checkpoint file. The calculation should converge in 45 steps. The frequency calculation tell us the nature of this critical point. Check all frequencies are positive so this corresponds to the ground state minimum.
You can notice that you get the energy of the different "level of calculation" :
ONIOM: calculating energy. ONIOM: gridpoint 1 method: low system: model energy: 0.052031674589 ONIOM: gridpoint 2 method: high system: model energy: -230.759360919005 ONIOM: gridpoint 3 method: low system: real energy: -0.011119897176 ONIOM: extrapolated energy = -230.822512490770
Input and output files
Media:s0_oniom_cas_631gd_am1.gjf
Media:s0_oniom_cas_631gd_am1.log
Calculate the S1 Frank-Condon vertical excitation energy
Calculation
The vertical excitation energies can be calculated from this optimised geometry. The force keyword can be used to provide information about the gradient of the potential energy surface at this geometry.
Keyword break
You must include nroot=x in the CAS keyword === > Calculations on excited states of molecular systems may be requested using the NRoot option. (Note that a value of 1 specifies the ground state, not the first excited state)
#p force oniom(casscf(6,6,nroot=2)/6-31g(d):am1) geom=check guess=read nosymm pop=full
Results
You should get this energy in the output file. Ensure that the orbitals have converged within a few iterations so that we know they have been read in correctly.
ONIOM: calculating energy. ONIOM: gridpoint 1 method: low system: model energy: 0.052034390477 ONIOM: gridpoint 2 method: high system: model energy: -230.585348680238 ONIOM: gridpoint 3 method: low system: real energy: -0.011115630772 ONIOM: extrapolated energy = -230.648498701486
The difference between the energy of the excited state and the ground state is:
ΔE = ES1FC - ES0min = 109.20 kcal/mol
Input and output fair
Media:s0s1_FC_oniom_cas_631gd_am1.gjf
Media:s0s1_FC_oniom_cas_631gd_am1.log
Optimise the geometry of the excited state minimum
Calculation
We will optimize the minimum on the S1 to be able to give the energy difference between the S1 minimum and the conical intersection.
#p opt freq oniom(casscf(6,6,nroot=2)/6-31g(d):am1) geom=check guess=read nosymm pop=full
Results
The geometry optimises in 12 steps with the following energies:
ONIOM: calculating energy. ONIOM: gridpoint 1 method: low system: model energy: 0.069184790617 ONIOM: gridpoint 2 method: high system: model energy: -230.589044508969 ONIOM: gridpoint 3 method: low system: real energy: 0.001053820476 ONIOM: extrapolated energy = -230.657175479110
Input and output files
Media:s1_oniom_cas_631gd_am1.gjf
Media:s1_oniom_cas_631gd_am1.log
Find the S1/S0 conical intersections
Advice break
Before beginning this part make sure that you read the part ONIOM for crossings.
In order to find the conical intersection we will start from the Franck-Condon geometry. As was done in the CASSCF tutorial, the planar structure of the benzene ring must be broken by moving one of the carbon atoms out of the plane as shown on the following picture. The molecule has C2 symmetry so there are three possible carbon atoms to move out the plane. This suggests that there may be multiple different S1/S0 crossings that can be located by the conical intersection optimization. The conical intersection you'll find depend on which carbon atom you've moved out of the plane and towards which direction...
Calculation
The fact that we are looking for a conical intersection is specified in the Opt=conical .
#p opt=conical oniom(casscf(6,6,nroot=2)/6-31g(d):am1) guess=read nosymm pop=full
Results
The geometry optimizes in 11 steps. The optimized geometry is the following :
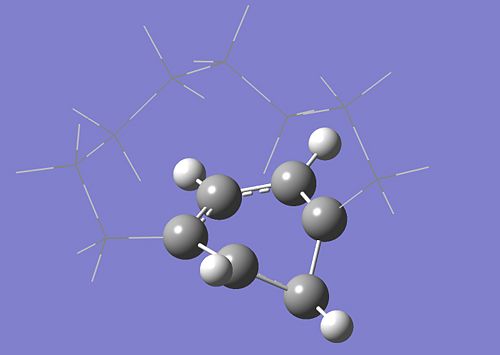
And the energy of this conical intersection is:
ONIOM: calculating energy. ONIOM: gridpoint 1 method: low system: model energy: 0.218401034221 ONIOM: gridpoint 2 method: high system: model energy: -230.568625411086 ONIOM: gridpoint 3 method: low system: real energy: 0.147379795087 ONIOM: extrapolated energy = -230.639646650220
The difference between the energy of the conical intersection and S1 is:
ΔE = ES0/S1CI - ES1min = 11.00 kcal/mol
Compare with the benzene alone
Some similar calculations was realized on benzene (you will be able to find the results here), and on an other molecule (Here)
So we can compare the difference between this 3 molecules.
What we hoped was that the fact that the cycle help to push the carbon out of the plan during the conical intersection optimization, so that the decrease compared to the benzene alone.
Input and output files
Media:s0s1_CI_oniom_cas_631gd_am1.gjf
Media:s0s1_CI_oniom_cas_631gd_am1.log
Back to ONIOM for excited states
Back to ONIOM for crossings
Back to ONIOM