La409Mod1

Laurence Archer - 3rd year Computational Chemistry laboratory

Introduction

The purpose of this investigation is to use computational calculations to model real-life chemical reactions and be able to explain the selectivity and spectroscopic properties observed based on the computed energetic and electronic properties. Initially this starts off as using 'Molecular Mechanics', which combines classical mechanical molecular interactions. The energies involved are:

• Stretch - based on Hooke's Law, representing the strain of stretching a bond from its equilibrium position
• Bend - analogous to Hooke's Law except for deviations in bond angle from equilibrium rather than extension
• Torsion - representing the torsional strain around a bond
• Electrostatic - based on Coulomb's Law, representing the electrical potential between two charged atoms
• Van der Waals - based on a 6-12 Lennard-Jones potential, representing dispersion forces between atoms

The MM2 and MMFF94 algorithms in ChemBio3D are used in this case.

Semi-empirical molecular orbital theory is then used to perform calculations. This method uses semi-empirical quantum chemistry to determine molecular orbitals and hence how they may interact to stabilise/destabilise the molecule. This method is more reliable and realistic than the previous molecular mechanical approximation because it is now well known that a lot of selectivity and reactivity in chemical reactions can be explained by orbital interactions. The PM6 and AM1 algorithms of the MOPAC interface in ChemBio3D are used in this case.

The investigation then finally turns to ab initio quantum mechanical calculations using density functional theory. This method is most accurate in determining the detailed electronic structure of the system, resulting in more realistic energy values. In Gaussian, the B3LYP method is used for optimisations apart from when prior to NMR predictions, in which the more appropriate mpw1pw91 method is used. In both cases: the 6-31G(d,p) basis set is chosen. These calculations are very time-consuming and so they were submitted as Gaussian input files to the SCAN supercomputer system for execution.

The hydrogenation of the cyclopentadiene dimer

Orbital overview of the exo and endo addition

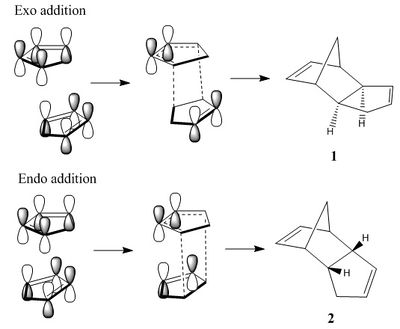
Introduction

Cyclopentadiene exists at room temperature in the more stable dimer form; monomeric cyclopentadiene can be obtained by 'cracking' of this dimer at high temperatures. The dimer can be formed by endo or exo [π4s + π2s] cycloaddition of the two monomers by the Diels-Alder mechanism. In the cycloaddition the HOMO of the diene attacks the LUMO of the dienophile by lining up the orbitals on top of each other. It can be seen in the image on the right that when endo addition occurs there is addition stabilising orbital overlap between the remaining two alkene's orbitals; this overlap is not present in the exo addition. Therefore, endo addition goes via a more stabilised transition state and is therefore the kinetic product. The purpose of this investigation is to model the two products and calculate the thermodynamic energies of each in order to determine the thermodynamic product.

The second part of the investigation is to determine which alkene in the endo product is the more thermodynamically favourable to undergo hydrogenation. This is done by modeling the two products and using molecular mechanics to calculate the relative energies.

Diels-Alder formation of dimeric cyclopentadiene

To determine which product is most thermodynamically stable the two forms were drawn in ChemBio3D and the minimum energy product found by iterative procedures of the MM2 molecular mechanics algorithm.

Structure energies of the exo and endo form of the cyclopentadiene dimer

Structure	Total energy	Stretch	Bend	Stretch-Bend	Torsion	Non-1,4 VDW	1,4 VDW	Dipole/Dipole
	31.8	1.3	20.6	-0.8	7.7	-1.4	4.2	0.4
	34.0	1.3	20.8	-0.8	9.5	-1.5	4.3	0.4

As can be seen by these energies the exo form is shown to be the more thermodynamically stable product. The main contributing factor to the higher energy in the endo form is the higher torsion energy, which derives from dihedral strain. In the endo form 2 one can see a noticeably worse 1,4 diaxial strain between the 'flat' cyclopentene ring and the 'bent' cyclopentene ring's alkene end than in comparison to the strain in the exo form 1 from the 'flat' cyclopentene ring with the 'norbornene' bridgehead.

Hydrogenation of the dimer

Hydrogenated products 3 and 4

Hydrogenation of the endo form with one equivalent of hydrogen can afford two different products (3 and 4) due to the two possible alkene sites of hydrogenation. To determine which double bond is the thermodynamically preferred site of hydrogenation the two product molecules were drawn in ChemBio3D and the minimum energy structure determined by the MM2 molecular mechanics method. The resulting data is tabulated below.

Structure energies of the two hydrogenated forms of the cyclopentadiene dimer

Structure	Total energy	Stretch	Bend	Stretch-Bend	Torsion	Non-1,4 VDW	1,4 VDW	Dipole/Dipole
	35.7	1.3	19.9	-0.8	10.8	-1.2	5.6	0.2
	31.2	1.1	14.5	-0.5	12.5	-1.1	4.5	0.1

As can be seen by these energies: Structure 4 is the more thermodynamically stable regioisomer. The key factor here is the lower bend energy in Structure 4, which can be attributed to the relief of the strained carbon-carbon double bond in the norbornene section of the dimer. An sp² carbon prefers to have a bond angle of 120° however the 'norbornene' alkene has a bond angle of 108° and the 'cyclopentene' has a bond angle of 112°. An additional result of hydrogenating the 'norbornene' alkene is not just relief of the C=C angle strain, but also the lowering of energy of some of the other norbornene vibrational-bending modes.

Stereochemistry and Reactivity of an intermediate in the synthesis of Taxol

Compounds 5 and 6

Introduction

Taxol is the trade name of the drug Paclitaxel, which is widely used in the treatment of lung, ovarian and breast cancer. In the synthesis of Taxol, an intermediate is formed that has been proposed to have one of the two atropisomeric forms: compounds 5 and 6. As can be seen: the orientation of the carbonyl is debated. In order to determine which form is more thermodynamically stable, molecular mechanical calculations were run on models of the two isomers. The MM2 calculation method was used as previously, but in addition the MMFF94 method was used too for comparison.

Analysis of the isomeric forms of the Intermediate

Structure energies of three isomers of the Taxol intermediate

Structure	Method	Total energy	Stretch	Bend	Stretch-Bend	Torsion	Non-1,4 VDW	1,4 VDW	Dipole/Dipole
	MM2	47.8	2.8	16.5	0.4	18.2	-1.5	13.1	-1.7
	MMFF94	60.7	-	-	-	-	-	-	-
	MM2	42.7	2.6	11.3	0.3	19.7	-2.2	12.9	-2.0
	MMFF94	60.6	-	-	-	-	-	-	-
	MM2	52.5	3.3	16.8	0.4	20.1	-0.1	13.8	-1.8
	MMFF94	74.8	-	-	-	-	-	-	-

It can be seen here that Structure 7 represents a high energy conformer which is thermodynamically unfavourable and is likely a minor isomer and in contrast: the low energy structures 5 and 6 are the major isomers of interest. The main difference in energy between Structures 5 and 6 is the bend energy. Measurement of the bond angles at the carbonyl carbon illustrates the degree of strain from normality (120°). Structure 6 is calculated to have a bond angle of 120° whereas Structure 5 has an angle of 126°, which explains the higher bend energy in the structure.

Hence the atropisomer with the carbonyl down (Structure 6) is shown to be the more thermodynamically stable isomer. This is in agreement with the literaure, whereby it was found that the carbonyl up structure is more energetically expensive.

The alkene by the bridgehead is already strained to a small degree from the ideal angle of 120°. Were the alkene to be hygrogenated to an alkane single bond, it can be calculated that the product does not have a vast change in angle between the bridgehead and the previously alkene C-C bond, instead as a result there is a large angle strain from ideal sp² geometry, and hence the hydrogenated product is unfavourable. This is the phenomenon of 'hyperstable akenes', whereby alkenes next to strained bridgeheads have a stabilisation related to the fact that hydrogenating would be an unfavourable reaction.

Semi-empirical MO theory modelling of the regioselective addition of dichlorocarbene

Introduction

Compound 8

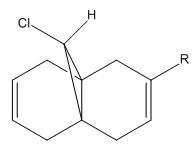
Compound 8 can be attacked by the electrophile dichlorocarbene on one of its two C=C π-bonds. The more nucleophilic π-bond, i.e. the major π-bond in the HOMO, is the one that is attacked by dichlorocarbene. A purely molecular mechanical approach to interpretting the reaction would result in concluding that the C=C bond anti/exo to the bridgehead chlorine is the preferred site of attack due to absence of steric clashes with the chlorine atom. However, here semi-empirical molecular orbital theory is employed to observe how orbital effects dictate the preferred regioselectivity.

Modelling of the Molecular Orbitals

In order to determine which C=C π-bond is attacked, the frontier orbitals of the system were calculated using the MOPAC/PM6 interface; the orbitals are ordered below. For this stage of the investigation hydrogen was used as the R group.

Molecular Orbitals of Compound 8

Orbital	MOPAC/PM6	Gaussian
LUMO +1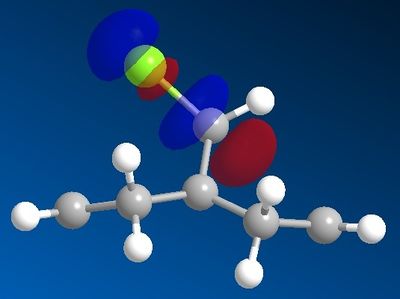
LUMO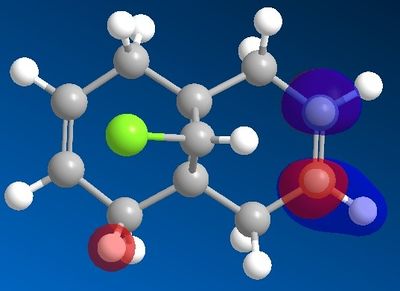
HOMO
HOMO -1

It can be seen that using the MOPAC interface does not produce entirely symmetrical orbitals even though energy minimalised structure has a clear plane of symmetry along the axis bisecting the two alkene bonds. For the purpose of interpreting the regioselectivity of the reaction in question: MOPAC calculations will suffice. However, more accurate orbitals can be calculated using ab initio Gaussian calculations, seen in the right-hand column of the above table. Symmetry parameters were input into Gaussian, allowing designation of the point group of the molecule as C_s, thus creating symmetric MOs.

The results indicate that the HOMO is mainly composed of the π-bond endo/syn to the chlorine on the bridge. By observing the LUMOs it can be seen that the C-Cl σ^* is relatively low energy (LUMO +1 by MOPAC's PM6 calculations; LUMO +2 by Gaussian) and able to overlap with the exo C=C π-bond, which means that the C-Cl σ^* is able to mix with the exo C=C π-bond, resulting in a weaker C=C bond but more stable molecular orbital. This π-bond then becomes less nucleophilic and the overall HOMO involving this π-bond of lower energy. As a result of these features, the electrophile will favour attack on the endo C=C bond.

These molecular orbitals are in good agreement with those in the literature.

Effect of the C-Cl bond on the key vibrational frequencies of the molecule

Compound 9

Compound 8 and a version (Compound 9) where the C=C bond anti to the chlorine has been hydrogenated were subjected to vibrational frequency analysis on Gaussian using the keywords: "# b3lyp/6-31G(d,p) opt freq". The aim was to observe the vibrational frequencies of the two structures and be able to relate any differences to the key bond energies and hence to the theory of C-Cl σ^*/C=C overlap. The IR spectra and relevant bond stretching frequencies are tabulated below.

Predicted IR spectrum of Compound 8

Predicted IR spectrum of Compound 9

	Bond energy / cm-1
	C=C (endo)	C=C (exo)	C-Cl	C-H (bridge)
Structure 8	1757	1737	771	3197
Structure 9	1758	na	775	3182

Initially focusing on just Structure 8, one can see from this data that the exo C=C bond has a lower bond energy. This is in agreement with the theory of the π-bond interacting with the C-Cl σ^*, which would result in weakening of the C=C π-bond. Comparing the C-Cl stretch of the diene (Structure 8) and the monoene (Structure 9) shows a small increase in energy in the C-Cl bond in the monoene. Since the monoene no longer contains the alkene bond that is proposed to interact with the C-Cl bond: no mixing occurs, no movement of electron density into the C-Cl σ^* orbital occurs and thus the C-Cl σ bond is stronger (less weakened). The C-Cl bond vibrational frequencies in the above table agree with this.

Effect of substituents on stretching frequencies

By varying the R group in Compound 8 one can alter the electron density in the C=C π bond and hence affect the key vibrational frequencies of the molecule. The aim is to see how changing the substituent between varying degrees of electron donating/withdrawing character will affect the bond energies of the C=C π-bond and the C-Cl σ-bond.

'R' substituent|	Bond energy / cm-1
	C=C (exo)	C=C (endo)	C-Cl	C-H (bridgehead)
BH2	1657	1757	759	3190
SiH3	1690	1756	763	3196
CN	1706	1757	765	3191
NO2	1739	1758	772	3187
NH2	1749	1756	766	3200
OH	1753	1758	765	3196

There is a good agreement between an increase in electron withdrawing strength of the R substituent and the weakening of the anti C=C bond and strengthening of the C-Cl bond. Lewis acidic groups such as -BH₂ have a strong withdrawing effect on the C=C π bond by accepting electron density into vacant orbitals, hence the bond energy of the C=C stretch is the lowest in the table. Electron donating groups such as NH₂ strengthen the C=C π-bond by resonance, as can be seen by the higher bond energy.

The agreement between higher electron density in the C=C π-bond resulting in weaker C-Cl bonds can be moderately correlated from the data. To take two extreme cases: NO₂ and NH₂, the electron withdrawing NO₂ group reduces the electron density in the C=C π-bond and therefore reduces the amount of interaction between the C=C π-bond and the C-Cl σ*-bond, thus less electron density occupies the anti-bonding C-Cl orbital and the bond is stronger. In NH₂ there is more electron density in the C=C π orbital and hence greater destabilisation of the C-Cl bond, resulting in a lower bond strength.

Modelling the 'neighbouring group participation' effect in glycosidation

Reaction scheme of nucleophilic attack on the oxonium compound with neighbouring group participation

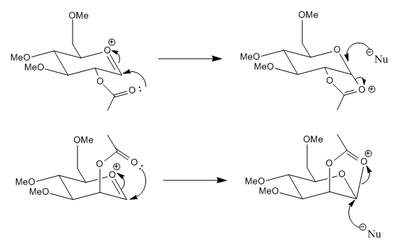
Introduction

Glycosidation is the process of replacing the group at the anomeric position in a sugar with a different nucleophile; the resulting anomeric glycosidic bond can be in the equatorial (β) or axial (α) position. This process is widely important in the field of carbohydrate chemistry where simple disaccharides are made by the formation of a glycosidic bond from the anomeric position on one monosaccharide to a different position on another monosaccharide. Control of the form of the anomeric glycosidic bond is important because this defines the sugar, e.g. α(1-4)Glu-Glu = Maltose, β(1-4)Glu-Glu = Cellobiose.

The presence of certain groups neighbouring the anomeric position results in high selectivity of α/β anomers during glycosidation due to these groups being able to interact with the intermediate oxonium ion. In the case here a lone pair on the carbonyl in the acetoxy group can attack the anomeric carbon, thus effectively completing the glycosidation process at the anomeric position, though a different and proposed to be more stable oxonium ion is formed which can decompose on attack with an external nucleophile at the anomeric carbon. The neighbouring group participation therefore is proposed to provide a lower energy pathway for glycosidation and hence rates of reaction are alot higher. Depending on the orientation of the acetoxy group, the external nucelophile will have only one favourable attack orientation.

The purpose of this investigation is to model the neighbouring group participation effect and perform computational calculations of the relative energies of the reactants and intermediates to prove the effect. A methyl group was used as the 'R' group in the structure because it is not so large as to result in excessive conformational flexibility and the time for computation is not demanding. Use of a hydrogen however would allow hydrogen bonds between the side groups, thus disrupting the interactions under study.

Neighbouring group participation

Four different orientations of acetoxy attack on the anomeric position were determined:

• Equatorial OAc attack from below (Structure A)
• Equatorial OAc attack from above (Structure A')
• Axial OAc attack from above (Structure B)
• Axial OAc attack from below (Structure B')

Data on the relative energies of Structures A, A', B & B'

Compound	Heat of Formation (PM6)	Total steric energy (MM2)	Stretch	Bend	Stretch-Bend	Torsion	Non-1,4 VDW	1,4 VDW	Charge/Dipole	Dipole/Dipole
	-91.7	20.3	2.3	8.5	0.8	2.0	-1.6	19.9	-18.1	6.6
	-76.6	32.7	2.2	9.0	0.8	1.4	-3.3	19.3	-0.8	4.0
	-88.7	12.8	2.4	10.6	0.9	3.0	-0.4	20.0	-31.1	7.5
	-75.4	16.1	2.2	10.5	0.8	1.8	-0.8	20.0	-23.5	5.6

The first point to notice from this data is that Structures A and B are lower in energy than Structures A' and B', respectively. The main difference in the MM2 calculated energies are due to the differing Charge/Dipole interaction energies which arise from interaction of the partially negatively charged carbonyl oxygen with the formally positively charged oxonium oxygen. The 'prime' versions involve an acetoxy group orientating themselves from one face of the ring to the other. As can be seen in the structures, the carbonyl oxygen on the acetoxy group in the 'prime' versions is further away from the oxonium cation due to this mentioned strain in 'reaching around' to the other face of the ring, hence the charge/dipole interaction energy is less negative than A & B.

The MOPAC PM6 method takes into account molecular orbital interactions, unlike MM2. A lone pair of electrons on the acetoxy carbonyl oxygen atom can interact, when aligned correctly, with the π* orbital of the bond between the anomeric carbon and oxonium oxygen, resulting in a stabilisation energy. In order to get good overlap the nucleophilic lone pair must be orientated at the Bürgi-Dunitz angle of 107° with the plane of the oxonium C=O bond, as this results in optimum overlap with the lobe of the π* orbital. The 'prime' versions of the structures, as mentioned previously, strain to reach around to the other face of the ring, which has the consequence of not allowing an ideal 107°. The angle between the carbonyl oxygen and the oxonium C=O plane was measured to be ~157° for the Structures A' and B', and 105° for Structures A and B. There is therefore better overlap in Structures A and B between interacting orbitals and hence a more stabilised energy, which can be observed in the data as the more negative heats of formation.

The second point to notice from this data is the lower MM2 energies in Structures B and B' relative to Structures A and A', and MOPAC PM6 heats of formation roughly equal to one another between these aforementioned pairs. The MM2 steric energies differ most with the Charge/dipole interaction energy. This can be attributed to the fact that Structures A and A' feature the acetoxy group in the equatorial position whereas Structures B and B' have the group in the axial position, where being in the equatorial position results in a much further distance between the carbonyl oxygen and the oxonium cation in comparison to when located axially, hence stabilising interactions cannot occur as well. The MOPAC PM6 energies do not differ much because the axial vs. equatorial preferential arguments are based on molecular mechanical interactions; the molecular orbital picture does not change much between the two forms.

Consequential nucleophilic attack

The structures corresponding to the result of acetoxy participation at the anomeric centre of Sturctures A, A', B and B' are denoted Structures C, C', D and D', respectively. The computed energies are tabulated below.

Data on the relative energies of Structures C, C', D & D'

Compound	Heat of Formation (PM6)	Total steric energy (MM2)	Stretch	Bend	Stretch-Bend	Torsion	Non-1,4 VDW	1,4 VDW	Charge/Dipole	Dipole/Dipole
	-91.7	25.2	2.0	12.9	0.7	8.3	-2.3	18.0	-11.9	-2.4
	-66.8	42.5	2.6	18.4	0.7	4.4	-3.2	18.5	2.2	-1.2
	-91.6	23.9	1.8	19.5	0.8	9.5	-2.2	18.0	-23.7	0.3
	-65.5	38.1	2.7	18.9	0.7	6.9	-2.4	18.9	-7.4	-0.3

It should be noted here that now in these structures: the 'acetoxy oxygen' has now become the oxonium cation, where previously the oxygen in the ring held the charge. It can be seen that in the structures of C and D the newly formed cyclic ring is orientated considerably above or below the main ring due to the connectivity to the main ring being via either two axial bonds or two equatorial bonds. This allows the oxonium oxygen to interact noticeably with the dipole of one of the methoxy groups around the ring, resulting in a highly stabilising (and thus more negative) charge/dipole interaction. In Structures C' and D' this interaction does not strongly occur because this new 5-membered oxonium ring is forced to orientate parallel and away from the main ring, due to one axial and one equatorial bond forming the ring. This means that structures C' and D' do not have this additional stabilisation, and hence have a higher overall energy. The MOPAC PM6 energies for C' and D' are less negative than the energies of C and D because the aforementioned strain results in a difficulty for the anomeric carbon to adopt ideal sp³ geometry, which is the optimal geometry for the molecular orbitals resulting from combination of atomic orbitals on the anomeric carbon and its substituents.

The MOPAC PM6 energies do not change between A & B and A' & B' because, as previously mentioned, the same molecular orbitals are interacting at effectively the same angles, hence the total molecular orbital interaction energy will not change. The MM2 steric energies can be noted to not differ much as well. Previously there was a large difference in charge/dipole energy, but that was due to axial acetoxy being physically closer to the oxonium than equatorial acetoxy, however now the two forms of the oxonium both lie equally close to differing ether groups that have rotational freedom to orientate in a way that promotes a dipole/charge interaction with the oxonium, hence there is little difference in the charge dipole interactions.

Conclusion

The calculations computed in this section have shown that when an acetoxy group is equatorial the thermodynamically favourable neighbouring group participation goes via attack on the anomeric carbon on the bottom face of the molecule, and so nucleophilic attack will occur from the top face, hence the β-anomer is formed. When the acetoxy is axial the thermodynamically favourable product after nucleophilic attack will be the α-anomer. It should be noted however that the α-anomer is more thermodynamically favourable than the β-anomer due to the anomeric effect, whereby orbital overlap of the oxygen in the ring's lone pair with the σ* orbital of the anomeric bond results in stabilisation. These conclusions are in good agreement with the literature.

Mini project

Compounds 10, ent-10 and 11

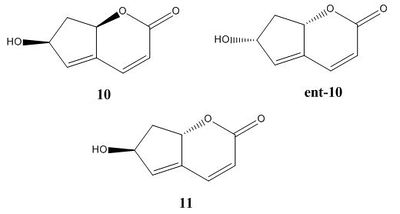
The aim of this project is to use density functional theory based molecular orbital methods to calculated spectroscopic data of isomers of a product found in the literature and show how this information may be used to differentiate between the two isomers. Gaussian 09W was utilised to perform ab initio molecular orbital calculations using a DFT basis set.

Krishna and Narsingam developed a method of total synthesis of the natural product: ilex lactone (isolated from Ilex aquifolium). The natural product occurs as Structure 10, which is synthesised via a ring closing metathesis using Grubbs' 2nd generation catalyst. Also detailed in the literature is the formation of the enantiomer and diastereomer of Structure 10 : Structures ent-10 and 11, respectively, which are the result of a Grignard addition to a carbonyl resulting in a mixture of two isomers.

Structure ent-10 had data only on its optical rotation in the literature, whereas structures 10 and 11 have full spectroscopic data, hence only optical rotation computational calculations were performed on the former, and full studies were performed on the latter two structures.

¹³C NMR spectrum prediction

The structure of the two compounds were optimised using Gaussian prior to prediction of spectroscopic information. The resulting structures are shown in the JMol files below.

These structures were subjected to the NMR prediction methods of Gaussian using the keywords:

# mpw1pw91/6-31(d,p) NMR scrf(cpcm,solvent=chloroform)

The Gaussian output was visualised in GaussView, yielding the spectra and data shown below. The carbonyl carbon had to be corrected using the formula: δ_corr = 0.96δ_calc + 12.2.

Computed NMR spectrum of 10

Computed NMR spectrum of 11

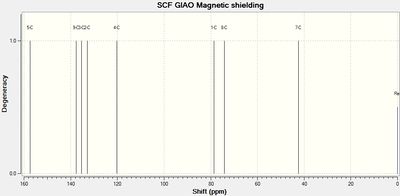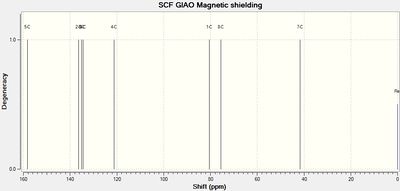Structure 10 NMR signals			Sructure 11 NMR signals
Lit. shift / ppm	Calc. shift / ppm	Assignment	Assignment	Calc. shift / ppm	Lit. shift / ppm
164	157 (154 corrected)	C5	C5	158 (154 corrected)	161
135	133	C2	C2	136	137
137	135	C3	C3	135	133
137	138	C8	C8	134	133
122	120	C4	C4	121	123
81	79	C1	C1	80	83
74	74	C7	C7	76	80
42	42	C6	C6	42	39

NMR assignments of 10

NMR assignments of 11

The key difference between the isomers in the calculated data is the change in chemical shifts of carbons 2 and 8. In Structure 10 carbon 8 is the most deshielded of the pair due to the electron withdrawing effects of the hydroxy group. However in Structure 11, the stereochemistry of carbon 1 inverts, thus resulting in the hydrogens on the neighbouring carbon 6 to move below the plane of the molecule. As an add-on effect, the carbon 7 hydroxy hydrogen is now able rotate so as to point towards the carbon 2-8 alkene bond, which results in a more shielded carbon 8, relative to carbon 2.

The calculated shifts are generally in good agreement with the literature, however the carbonyl carbon is seen to be noticeably more deshielded than calculated. This is likely due to over-estimation of the donating effects of the enone alkene and the lactone oxygen to the carbonyl, hence resulting in a more shielded theoretical shift.

³J H-H coupling in the compounds

The coupling constants of the ³J coupling present in Compounds 10 and 11 were calculated using Janocchio. The spectrometer frequency was set as 300 MHz. The calculated values are tabulated below.

Coupling constants

Coupling protons	Compound 10		Compound 11
	Calculated / Hz	Literature / Hz	Calculated / Hz	Literature / Hz
H(C3) - H(C4)	8.21	9.63	8.21	9.63
H(C7) - H(C6)	8.73/8.07	7.55	6.57/1.16	6.79

Agreement between calculated and literature is moderate for the alkene hydrogens (where the alkene bond is between C3 and C4). The agreement is good for the coupling of the hydrogen on C7 to the two hydrogens on C6. The calculation for Compound 11 predicts a low coupling constant for the hydrogen on C6 cis to the hydroxy due to the dihedral angle between this proton and the one on C7 being 92°, which according to the Karplus equation: will have a very low ³J coupling constant.

There is a noticeable difference in the H(C7)-H(C6) coupling constant between Compound 10 and 11, which could potentially be used to differentiate between the isomers.

IR vibrational spectrum prediction

Analysis of the vibrational modes of a molecule can be done by invoking the keyword "freq" in the calculation method parameters. In this investigation the full set of parameters were:

# b3lyp/6-31G(d,p) opt  freq

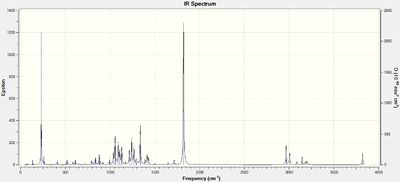
The resulting IR spectra are shown below

IR spectrum of Compound 10

IR spectrum of Compound 11

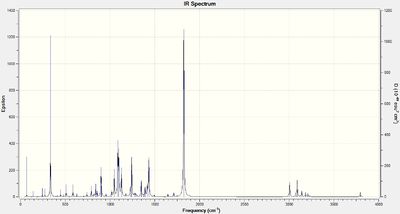Bond	Compound 10 stretching frequencies / cm-1		Compound 11 stretching frequencies / cm-1
	Calculated	Literature	Calculated	Literature
C=C	1715	1720	1712	1720
C=O	1821	na	1823	na
C-H (CH2 on C6)	3087	3090	3090	3093

It can be seen here that there is little difference between the IR spectra of the two isomers Compound 10 and 11. The calculated values are in good agreement with the literature, likely due to the fact that the structures are not very conformationally flexible and hence the optimised structure is a close representation of the experimental structure.

Optical rotation prediction

The optical rotation of Compounds 10, ent-10 and 11 were calculated on Gaussian by using the Cambridge version of the B3LYP density functional method. The parameter keywords were:

# cam-b3lyp/ 6-311G(d,p) polar(optrot) scrf(IEFPCM,solvent=chloroform) CPHF=RdFreq

Optical rotation, α_D

Compound	Calculated	Literature
10	-632	-80.6
ent-10	+632	+80.0
11	+148	-8.7

The magnitude of the optical rotations are in poor agreement with the literature. However, the two enantiomers can be distinguished through their value's opposite polarity but with equal magnitudes. Because the magnitude of the rotations of 10 and ent-10 are so far off the literature, and because the literature for 11 is close to 0, the calculated rotation for 11 can be 'understood' for having the wrong polarity. The excessively large magnitude of the optical rotation is likely due to the fact that the compounds have a large degree of conjugation, where conjugated/aromatic structures are known to have optical rotations computed at high values.

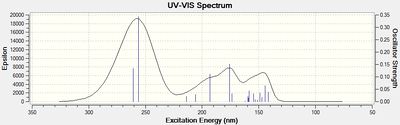
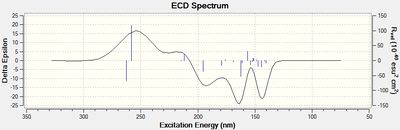
Electronic Circular Dichroism (CD/UV-Vis) spectrum prediction

The Circular Dichroism spectrum was generated by Gaussian using the following parameters:

# cam-b3lyp/6-311G(d,p) td(NStates=20) scrf(IEFPCM,solvent=chloroform)

This uses again the Cambridge version of the B3LYP basis set, with a time-dependent DFT method.

UV spectrum of Compound 10

UV spectrum of Compound 11

There is a negligible difference in the UV-Vis spectra of the two compounds and hence could not be used to differentiate between the two isomers.

ECD spectrum of Compound 10	ECD spectrum of Compound 11
ECD spectrum of Compound ent-10

The ECD spectrum shows a noticeable difference. Circular dichroism spectroscopy involves incidence of circularly polarised light on the sample, where light in one orientation is absorbed more strongly than in the other for chiral compounds. The measured property in the spectra is 'delta ε', which refers to the difference in absorption between light polarised in the left and right direction, hence for chiral compounds this is non-zero. It can be seen in the CD spectra the two differing chiral centres by the two unique regions of the spectra; a broad peak is seen at ~260nm with a Δε that changes from negative to positive between 10 and ent-10, keeping the magnitude unchanged at ~23. The second peak occurs at ~140-160nm, again changing polarity on going between the two enantiomers. The main feature of this peak is that it briefly shoots up/down at ~150nm, changing polarity. This feature does not occur in the CD spectrum of the diastereomer 11. Hence the spectra show the ability of Circular Dichroism spectroscopy to differentiate between the two enantiomers. Although there is a change in the spectrum between 10 and 11, the Δε values cannot be correlated to each other.

Conclusions of the Module

It has been shown here that computational chemistry is an invaluable tool for prediction of thermodynamically favourable isomers and structures. For simple structures where there are no likely low-lying LUMOs (e.g. σ* C-Cl, σ* C-O) orientated for possible interaction with other orbitals, molecular mechanical methods will suffice in determining relative energies. When there is the possibility of these interactions occurring then there is the need to incorporate Molecular Orbital Theory into the calculations. For less time consumption, semi-empirical MO theory methods such as MOPAC PM6/RM1 may be used, however one of the flaws of this method have been found in Section 4.2 of this report, whereby MOPAC will not product symmetrical orbitals and the energetic ordering of the molecular orbitals can be different to the order determined by the ab initio quantum mechanical methods used in Gaussian. These ab initio density functional theory calculations take a much longer time to compute, but produce highly reliable and accurate results, hence this method is the most widely preferred.