LUT1234

This is a year 1 project for the Molecular Modelling 2 course

NH₃ Model

Optimisation

The following information was obtained when a molecule of NH₃ was optimised in Gaussview. It was run in order to find the final energy of the molecule and the bond angles/lengths of the minimised structure.

Information	Data
Molecule	NH3
Calculation Method	B3LYP
Basis Set	6-31G(d,p)
Final Energy (a.u.)	-56.55776762
RMS Gradient	0.00032440
Point Group of Molecule	C3V
Bond Lengths (Å)	1.01798
Bond Angle (Degrees)	105.741

The optimisation went to completion as the values below went below the threshold. This means that the lines converged on zero.

Item	Value
Maximum Force	0.000004
RMS Force	0.000004
Maximum Displacement	0.000072
RMS Displacement	0.000035

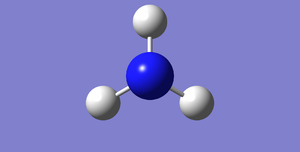
Images of the optimised molecule

The images of the optimised NH₃ can be seen below. The first image can be rotated and the data that leads to this image can be found in the link below.

NH3 molecule

The optimisation file is linked here

This shows the final NH3 molecule once it had been optimised.

This image shows the vibrational modes and frequencies and their relative intensities of an NH3 molecule.

Questions on the vibrational mode of the NH₃ molecule

This section answers the questions raised in the lab script and adresses the reason as to why the charges on the N and H atoms differ.

Question	Answer
How many nodes do you expect from the 3N-6 rule?	From this rule, and the fact we have 4 atoms, we would expect 6 vibrational modes.
Which modes are degenerate (ie have the same energy)?	The modes that are degenerate have the same energy. These are due to the fact that these are in fact the same vibrations, but using a different pairing of hydrogen's.
Which modes are "bending" vibrations and which are "bond stretch" vibrations?	1, 2 and 3 are due to bending and 4, 5 and 6 are due to stretching.
Which mode is highly symmetric?	Number 4 is highly symmetric
One mode is known as the "umbrella" mode, which one is this?	Number 1 is the umbrella mode
How many bands would you expect to see in an experimental spectrum of gaseous ammonia?	2 bands. The other 2 bands have such a small peak that they would not be seen

Atom	Charge	Expectations
N	-1.125	The expectation would be for the nitrogen atom to have a slight negative charge attached to it. This is because it is more electronegative than the hydrogen atoms.
H	0.375	The expectation would be for the hydrogen atoms to have a slight positive charge attached to them. This is because they are less electronegative than the nitrogen atom. This charge would have a third of the value of the nitrogen atom as it is a neutral molecule overall.

N₂ molecule

The following information was obtained when a molecule of N₂ was optimised in Gaussview. The molecule was optimised in order to make sure that the molecule was in a global minima.

Information	Data
Molecule	N2
Calculation Method	B3LYP
Basis Set	6-31G(d,p)
Final Energy (a.u.)	-109.52359111
RMS Gradient	0.02473091
Point Group of Molecule	D*H
Bond Lengths (Å)	1.09200

The optimisation went to completion as the values below went below the threshold. This means that the lines converged on zero.

Item	Value
Maximum Force	0.000001
RMS Force	0.000001
Maximum Displacement	0.000000
RMS Displacement	0.000000

Mode	Frequency
1	2457.33

Images of the optimised N₂ molecule

The images below show the optimised N₂ molecule. The first model is in three dimensions so can be manually rotated. However, this image only appears to have one bond, whereas the static image shows three. The link to the file is provided.

N2 molecule

The optimisation file is linked here

Charges and Vibrational modes

There are no charges on this molecule as they are the same atom, so same electronegativity. This means that only one vibrational mode would be expected. This is proven to be the case by by the prediction given by the program shown below.

This shows however, that this vibrational mode would not appear on an infra-red spectrum as it has minimal signal strength.

Molecular Orbitals

The diagrams below show the pi and sigma molecular bonding orbitals in an N₂ molecule. These are a combination of the 2p atomic orbitals. There are no visible distortions in the molecular orbitals. This is due to the fact that both atoms have the same electronegativity as they are the same element, and so the electon cloud will be evenly distributed between the two.

H₂ molecule

Images of the optimised H₂ molecule

The following information was obtained when a molecule of H₂ was optimised in Gaussview. This was done in order to find the global minimum for the energy of the molecule.

Information	Data
Molecule	H2
Calculation Method	B3LYP
Basis Set	6-31G(d,p)
Final Energy (a.u.)	-1.17853936
RMS Gradient	0.00000017
Point Group of Molecule	D*H
Bond Lengths (Å)	0.74279

The optimisation went to completion as the values below went below the threshold. This means that the lines converged on zero.

Item	Value
Maximum Force	0.000000
RMS Force	0.000000
Maximum Displacement	0.000000
RMS Displacement	0.000001

Vibrational Modes

The only vibration in an H₂ molecule is shown below. Only one would be expected but due to its very low signal output, this would not show up on an infra-red spectrum.

The vibrational modes that are found in H2

Mode	Frequency
1	4465.68

Images of optimised H₂ molecule

The following images were produced from the optimisation. These images have the correct bond length and the file used to create these images has been linked.

H2 molecule

The optimisation file is linked here

The optimised H2 molecule.

Charges on individual atoms of the molecule

There are no charges on this molecule as they are the same atom, so they same electronegativity and will not distort the electron cloud.

Haber - Bosch process

Enthalpy of Reaction

Bond type	Number of Molecules	Energy of bonds
NH3	2	-113.11553524
N2	1	-109.52359111
H2	3	-3.53561808

Therefore, the overall energy of the reaction = -0.05632605 Au

And so in kJ = -147.884044275 kJ mol^-1

Therefore ammonia is more stable than hydrogen and nitrogen gas.

Carbon Monoxide

Optimisation of CO molecule

The following information was obtained when a molecule of CO was optimised in Gaussview. It was optimised so that the bond energy and length would be correct.

Information	Data
Molecule	CO
Calculation Method	B3LYP
Basis Set	6-31G(D,P)
Final Energy (a.u.)	-113.30945314
RMS Gradient	0.00001828
Bond Lengths (Å)	1.13793
Point Group	C*V

The optimisation went to completion as the values below went below the threshold. This means that the lines converged on zero.

Item	Value
Maximum Force	0.000032
RMS Force	0.000032
Maximum Displacement	0.000011
RMS Displacement	0.000018

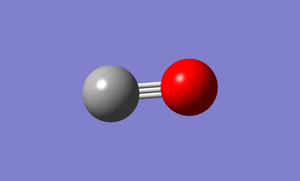
Images of Optimised molecule

The images of the optimised carbon monoxide molecule have been placed below along with the raw data file.

CO molecule

The optimisation file is linked here

This shows the optimised CO molecule.

Vibrational Modes

Only one form of vibrational mode will be present in a carbon monoxide molecule. This will be visible on an infra-red spectrum. The predictions that the programme makes for this vibrational mode can be seen below.

This shows the vibrational modes in the optimised CO molecule.

Charge distribution

The carbon monoxide molecule will have an uneven charge distribution on the oxygen and carbon atoms due to the fact that the oxygen atom is more electronegative than the carbon atom. This will cause the electron cloud to be distorted so that the electrons are more likely to be found around the oxygen atom.

The CO molecule has an uneven distribution of charge. The values of the charge are shown on the respective atoms, oxygen being the negatively charged atom due to its greater electronegativity.

Molecular Orbital diagrams for carbon monoxide

The molecular orbitals in a molecule of carbon monoxide will be distorted by this difference in electronegativity. The following molecular orbitals show this. These diagrams are the programmes predictions for the effect on different molecular orbitals;

This 3 sigma molecular orbital shows the interaction between the two 2S orbitals. The major lobe of this orbital is centered around the oxygen atom. This will be due to the fact that the oxygen is the more electronegative atom.

The 4 sigma * orbital shows the anti bonding orbitals between the two 2S orbitals. The major lobe has formed around the carbon atom as it has a 2S orbital higher in energy and therefore will influence the shape of the molecular orbital more.

This molecular orbital, one of the 1 pi orbitals, shows the formation of the pi bond that is part of the triple bond. It is formed from the overlap of two 2p orbitals. The oxygen has greater influence on the orbital shape as it is the more electronegative atom.

This shows the 5 sigma bonding orbital between two of the 2p orbitals. The diagram clearly shows the oxygen atom has a greater influence on the molecular orbital as the electron density has a greater probability of being located around the oxygen atom.

This is the LUMO. It is the 2 sigma* orbital. The orbitals are out of phase and there is no overlap.

Further molecular orbital diagrams

As the size of the molecular orbitals became larger, the distortion on the molecular orbitals become more pronounced. As further research into this, the molecular orbitals for higher interactions were plotted.

Despite the clear indication in this 11 sigma* orbital that the molecular orbital is influenced by the carbon, there is no way of telling whether this distortion is bigger than those molecular orbitals that are actually involved in the molecular bonding.