KSM214

NH₃ molecule

The following information summarizes the the NH₃ molecule that I have optimized using the Gaussian tool.

Analysis

Summary

Molecule	NH3
Calculation method	FREQ
Basis set	6-1G(D.P)
Final energy	-56.55776873 a.u.
RMS gradient	0.00000485 a.u.
Point group	C3v
Bond length	1.01798 Å
Bond angle	105.74118°

Item Table

Item	Value	Threshold	Converged?
Maximum Force	0.000004	0.000450	YES
RMS Force	0.000004	0.000300	YES
Maximum Displacement	0.000072	0.001800	YES
RMS Displacement	0.000035	0.001200	YES

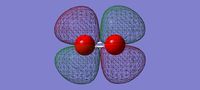
3D image of the NH₃ Molecule

NH Molecule

The optimisation file has been linked here

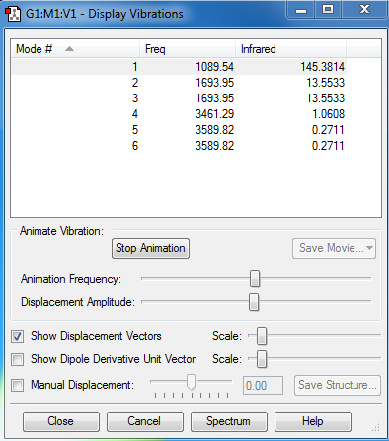
Molecular Vibrations

===Vibrations and Charges===

Number of modes to be expected:	6
Degenerate modes:	2,3 and 5,6
Bending vibrations:	1,2,3
Stretching vibrations:	4,5,6
Symmetric mode:	4
Umbrella mode:	1
Bands expected:	2
Charge on Nitrogen atom:	-1.25
Charge on Hydrogen atom:	0.375

N₂ Molecule

The following information summarizes the the N₂ molecule that I have optimized using the Gaussian tool.

Analysis

Summary

Molecule	N2
Calculation method	RB3LYP
Basis set	6-3-1G(d.p)
Final energy	-109.52412868 a.u.
RMS gradient	0.00000060 a.u.
Point group	D*H
Bond length	1.10550 Å
Bond angle	180°

Item Table

Item	Value	Threshold	Converged?
Maximum Force	0.000001	0.000450	YES
RMS Force	0.000001	0.000300	YES
Maximum Displacement	0.000000	0.001800	YES
RMS Displacement	0.000000	0.001200	YES

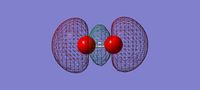
3D image of the N₂ molecule

N Molecule

The optimisation file has been linked here

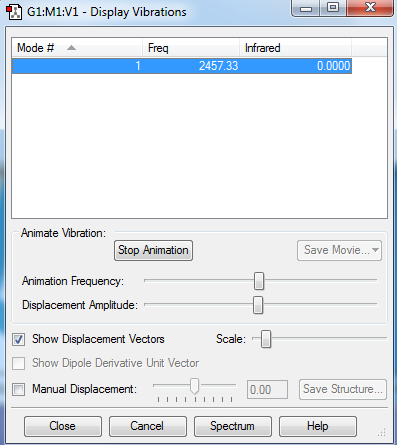
Molecular Vibrations

The N₂ molecule being a diatomic molecule has a charge equal to zero.

H₂ Molecule

The following information summarizes the the N₂ molecule that I have optimized using the Gaussian tool.

Analysis

Summary

Molecule	H2
Calculation method	RB3LYP
Basis set	6-3-1G(d.p)
Final energy	-1.17853936 a.u.
RMS gradient	0.00000017 a.u.
Point group	D*H
Bond length	0.74279 Å
Bond angle	180°

Item Table

Item	Value	Threshold	Converged?
Maximum Force	0.000000	0.000450	YES
RMS Force	0.000000	0.000300	YES
Maximum Displacement	0.000000	0.001800	YES
RMS Displacement	0.000001	0.001200	YES

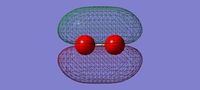
3D image of the H₂ molecule

H Molecule

The optimisation file has been linked here

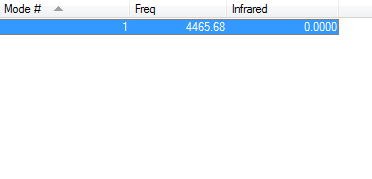
Molecular Vibrations

The H₂ molecule being a diatomic molecule has a charge equal to zero.

Energy Calculations for the Haber-Bosch process

The Haber-Bosch process is a reaction in which nitrogen gas and hydrogen gas are converted to ammonia. It is an extremely important reaction within the farming industry as a fertilizer.

N_2(g) + 3H_2(g) → 2NH_3(g)

The Enthalpy of the reaction has been calculated below using the table of results that I have acquired from the summary data of the optimized molecules.

Energies

E(NH3)	-56.55776873 a.u.
2*E(NH3)	-113.1155374 a.u.
E(N2)	-109.52412868 a.u.
E(H2)	-1.17853936 a.u.
3*E(H2)	-3.53561808 a.u.
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]	-0.05578994
ΔE	-146.476 kj/mol

O₂ Molecule

The following information summarizes the the O₂ molecule that I have optimized using the Gaussian tool.

Analysis

Summary

Molecule	H2
Calculation method	FREQ
Basis set	6-3-1G(D.P)
Final energy	-150.25742434 a.u.
RMS gradient	0.00007502 a.u.
Point group	D*H
Bond length	1.21602 Å
Bond angle	180°

Item Table

Item	Value	Threshold	Converged?
Maximum Force	0.000130	0.000450	YES
RMS Force	0.000130	0.000300	YES
Maximum Displacement	0.000080	0.001800	YES
RMS Displacement	0.000113	0.001200	YES

3D image of the O₂ Molecule

O Molecule

The optimisation file has been linked here

Molecular Vibrations

Molecular Orbitals

Molecular Orbitals for the O₂ Molecule

O2 1st MO	This is the 1sσ orbital containing paired electrons of the lowest energies.
O2 2nd MO	This is the 1sσ* orbital containing paired electrons.
O2 3rd MO	This is the 2sσ orbital containing paired electrons.
O2 4th MO	This is the 2sσ* orbital containing paired electrons.
O2 5th MO	This is the 2pσ orbital containing paired electrons of the 2px orientations interacting with one another.
O2 6th MO	This is the 2pπ orbital containing paired electrons of the 2py bonding orientation, being at a higher energy level than the 2px due to a conflicting arrangement in space in regards to electron density.
O2 7th MO	This is the 2pπ orbital containing paired electrons of the 2pz bonding orientation, being at a higher energy level than the 2px due to a conflicting arrangement in space in regards to electron density.
O2 8th MO	This is the 2pπ* orbital containing an unpaired electron of the 2py anti-bonding orientation, being at a lower energy level than the anti-bonding 2px orbital due to a preferential electron density arrangement.
O2 9th MO	This is the 2pπ* otbital containing an unpaired electron of the 2pz anti-bonding orientation, being at a lower energy level than the anti-bonding 2px orbital due to a preferential electron density arrangement.

Molecular Orbital Diagram for the O₂ Molecule

In accordance with the Aufbau principle and Hund’s rule the Oxygen Molecule follows the trend of filling consecutive quantum numbers, (n, l, ml, ms), of lowest energies and increasing until all electrons are contained within orbitals. However, having two electrons in the same orbital is energetically unfavorable because like charges repel. Thus, the parallel arrangement, thanks to the Pauli principle, has lower energy. Such a principle is evident in the 2π* orbitals in which the parallel arrangement is energetically favorable. The MO diagram correctly predicts two unpaired electrons in the π* orbital and a net bond order of two ( valence electrons: 8 bonding electrons and 4 antibonding electrons). The multiplicity in regards to the MO visualisation was initially set at '1' which would provide only paired electrons that would not reflect the correct correspondence to the true MO diagram for the oxygen molecule. However, when the Multiplicity was altered to '3', this allowed for unpaired electrons and so provided an accurate representation that would prove energetically favorable with the parallel arrangement in the 2π* orbitals.