KM01494984

2nd Year Molecular Reaction Dynamics Lab

Exercise 1

Q1

On a potential energy surface diagram, how is the transition state mathematically defined? How can the transition state be identified, and how can it be distinguished from a local minimum of the potential energy surface?

Transition state on a Potential Energy Surface

Distance vs Time plot

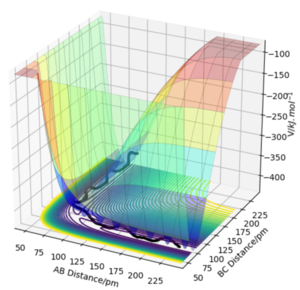
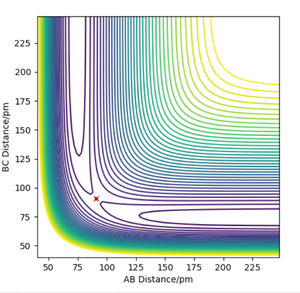
The transition state can be simply defined along a reactant to product pathway on a potential energy surface. Overall at the two minima, (corresponding to the reactants and products), the derivative of Potential energy ($\frac{dV}{dr}$) with respect to both r₁ (distance A-B) and r₂ (distance B-C) is 0. The transition state is defined as a saddle point, where the second derivative is positive in one direction and negative in the other ( therefore it's a local maxima at one end and a local minima at the other). As a result, it's defined as a maximum along this minimum energy pathway and as a minimum along the orthogonal diagonal line. Furthermore it can be simply identified through this rolling ball analogy where we start at the transition state on the surface plot ( potential energy surface). Upon addition of slight momentum, the ball would roll downwards towards a minima and oscillate there for a period of time. This idea of applying momentum can be understood as changing the geometry of the transition state by a small amount in the direction of the product to roll towards the products ( this same concept applies for the reactants).

Good. Mak214 (talk) 14:32, 24 May 2020 (BST)

---

Q2

Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” plot for a relevant trajectory.

Contour plot with the identified transition state position

Internuclear Distance vs Time

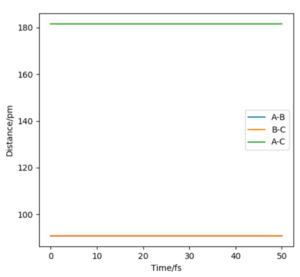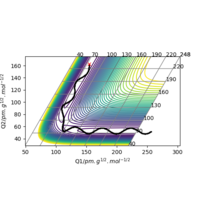
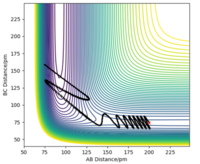
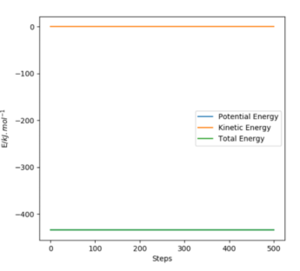
Since the H + H2 surface is symmetric, the transition state must have the conditions of r1 = r2. From the contour plot of the AB distance against the BC distance, there is no gradient in the direction at right angles to the ridge ( thus the trajectory will oscillate on the ridge and would never fall off). This idea can be used to find the transition state. The transition state position was estimated via such r values which would enable as little oscillation as possible. From this, the transition state was found to be located at 90.78 pm. A plot of "Internuclear Distance vs Time" was sketched to verify minimal oscillation at the selected r value (shown above)

Well done. Mak214 (talk) 14:34, 24 May 2020 (BST)

---

Q3

Comment on how the mep and the trajectory you just calculated differ.

Reaction proceeding via a minimum energy pathway

Reaction path calculated via dynamics instead of using the MEP

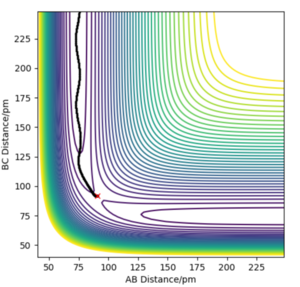This minimum energy pathway shows little oscillation along it's flight of path. However, this is inaccurate as atoms have a mass and (in the gas phase) there motion would be inertial. In calculating the reaction pathway via dynamics instead of the MEP, we therefore achieve a more realistic result with subtle oscillation along it's flight of path. It's important to note that the same initial conditions have been used in both cases (r1=91.78 pm and r2=90.77 pm).

---

OK. For the MEP calculation we reset the momenta to 0 at every step, this means the trajectory will go to the nearest minimum on the potential energy surface and then stop moving - its a useful way to find minima on a potential energy surface. Mak214 (talk) 14:38, 24 May 2020 (BST)

Q4

The table below illustrates plots of various trajectories and a description along their path of flight

p1	p2	Etot	Reactive?	Illustration of the trajectory	Description of the dynamics
-2.56	-5.1	-414.28	Yes		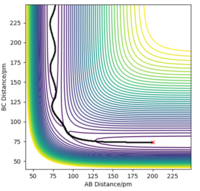The reaction smoothly proceeds from A + BC to AB + C. There is a greater oscillation in the reaction pathway beforehand, and this transitions into a smoother flight of path afterwards. This is because BC has a greater internal vibrational energy associated with it than AB.
-3.1	-4.1	-420.007	No		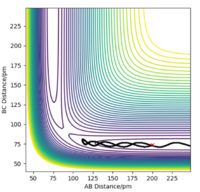This reaction doesn't occur as there isn't enough kinetic energy to overcome the activation barrier associated with this reaction. The "A" species doesn't approach the diatomic molecule (BC) with enough energy. As a result, the "A" species simply bounces off rather than reacting.
-3.1	-5.1	-413.977	Yes		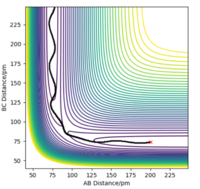The "A" species has enough kinetic energy to overcome this activation barrier and thus react to form the species "AB" and "C".
-5.1	-10.1	-357.277	No		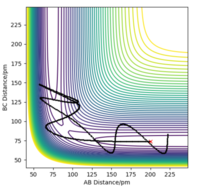Here, there was a case of barrier recrossing . This involves an initial surpassing of the transition state of the reaction ( as seen clearly in the diagram where new bonds begin to form), however the reaction then immediately reverses to reform it's initial starting reactants. Therefore, the reaction hasn't gone to completion and the final product is just the "A" and "BC" species.
-5.1	-10.6	-349.477	Yes		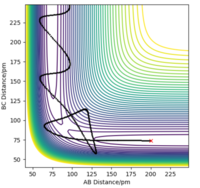Here, there is a temporary oscillation at the transition state before the reaction eventually proceeds over this activation energy barrier to form the products. Therefore, there is enough energy in the system to overcome the activation barrier at this trajectory and the H-F bond thus forms.

---

Q5

Given the results that have been obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?

The transition state theory prediction would be less accurate, as the model itself is based on multiple key assumptions which aren't always valid. Firstly, to estimate R_cl (average transmission rate/ frequency), the theory assumes that all trajectories with kinetic energy along the reaction coordinate greater than the activation energy will be reactive. But this isn't necessarily true as we saw in question 4. Furthermore, it assumes that the intermediates themselves lasts long enough to model the kinetic energy via Boltzmann distribution. Moreover, the theory itself oscillates between modelling via quantum mechanics ( treating energy as quantized) and classical mechanics ( when considering the motion of the system across the barrier in the reaction coordinate, essentially ignoring this idea of quantum tunnelling occurring). Overall, the reaction rate calculated via transition state theory may be slightly different then the experimental value due to these key approximations used to simplify the equation used . A clearer discussion was needed here that linked your reading about transition state theory (TST) to the results in your table above. Specifically if we look at your fourth trajectory we see that the postulate of TST which states that any system which crosses into the transition state WILL form the products is untrue. We can conclude that TST overestimates the rate of reaction as some collisions which cross the TST will not proceed to form the products. There may be some discussion of quantum tunnelling which is overlooked by TST - but not modelled in this experiment - that would have the effect of increasing the rate of reaction relative to a predicted rate by TST. Mak214 (talk) 14:45, 24 May 2020 (BST)

---

Exercise 2: The F - H - H system

Q1 - Potential Energy Surfaces

Via inspection of the Potential Energy Surfaces, classify the F + H₂ and H + H_F reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?

The potential energy surface of two hydrogen atoms reacting with a fluorine atom

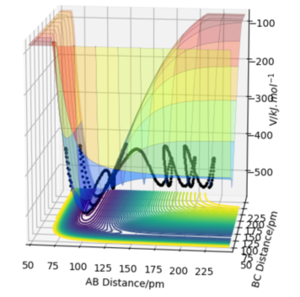
The F + H₂ is an exothermic reaction and H + HF is therefore endothermic. This can be understood from the relative energies of the reactants and products on the potential energy surface. From the diagram, one can identify that the bond energy of the H-F bond is greater than that of the H-H bond energy ( note A=F, B=H, C=H). The bond energy is a measure of the chemical bond strength, where a greater energy leads to a greater bond strength. Therefore, as the H-F bond strength is greater than that of the H-H bond, the F + H₂ reaction can be defined as exothermic. Great. Mak214 (talk) 14:45, 24 May 2020 (BST)

---

Q2

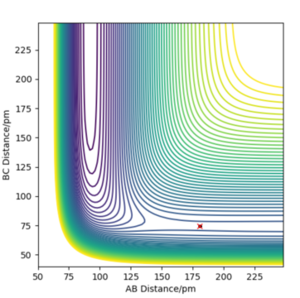
Locate both the approximate positions of the transition states and the activation energies for both reactions

Transition State Position

Energy vs Time Plot

Overall at the two minima, (corresponding to the reactants and products), the derivative of Potential energy ($\frac{dV}{dr}$) with respect to both r1 (distance A-B) and r2 (distance B-C) is 0. For this particular example, we can use Hammond's Postulate to define the transition state as it's incredibly short lived. This approximation enables use to draw comparisons between the transition state and the reactant ( or product) dependent on the energetic of the reaction. As this F + H2 forward reaction is exothermic, it has a early transition state and thus can be compared to that of the reactant. As a result, the transition state can be found to be located at (AB) H-H Distance = 0.744Å and (BC) H-F Distance at 1.811Å. Good. Mak214 (talk) 14:51, 24 May 2020 (BST)

Contour plot of the minimum energy pathway for H2 +F

Energy vs Time of the minimu energy pathway trajectory

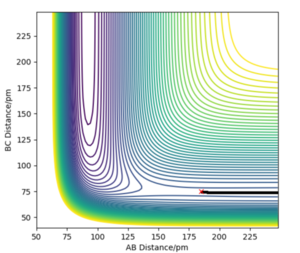
There appears to be an issue with "Contour plot of the minimum energy pathway for H2 +F". Maybe I'm the only one seeing it. Fdp18 (talk) 18:03, 24 May 2020 (BST)

Contour plot of the minimum energy pathway for H2 +F

Energy vs Time of the minimu energy pathway trajectory

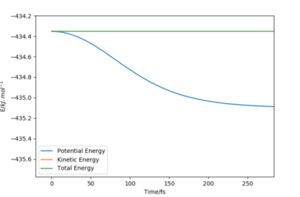
The activation energy can simply be found from the difference in the potential energy of the individual species ( understood through manipulating Hammond's postulate as explained above). Therefore, the activation energy for H2 + F is 0.238 kcal/ mol and 29.61 kcal/ mol reverse (H + HF). Good!! Mak214 (talk) 14:51, 24 May 2020 (BST)

---

Q3-Reaction Dynamics

Identify a set of initial conditions that results in a reactive trajectory for the F + H2, and look at the “Animation” and “Momenta vs Time”. In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. Explain how this could be confirmed experimentally.

Momenta vs Time graph

A set of initial conditions that results in a reaction trajectory for the F + H2 reaction is AB (F-H) being 200 pm and BC (H-H) Distance being 74 pm. The momentum for both the bonds is -1. To answer the question, we will look at the reaction between the diatomic H2 and a single fluorine atom. Initial there is a steady oscillation of the BC bond, representative of the vibrational bond energy associated with this diatomic hydrogen ( which can be modelled via a simple harmonic oscillator). After the collision, the BC bond has broken and a new AB bond has formed. This can be seen in the spike in the amount of oscillation of this new AB bond. The reaction is exothermic and energy must be conserved in this system. Therefore, this energy gained is simply lost through internal vibrational relaxation to the surrounding environment as heat energy. Experimentally, this can simply be monitored through the increase in temperature associated with the reaction ( as it's exothermic). What about translational energy? How would you distinguish between translational and vibrational energy by measuring the temperature change, we were looking for the name of an experimental technique. Mak214 (talk) 14:58, 24 May 2020 (BST)

---

Q4

Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.

pHH	Illustration of the trajectory	Description of the dynamics
-6.10		Initially, the hydrogen molecule begins to vibrate and the system approaches the transition state, however there isn't enough energy to over come this reaction barrier and the reaction thus simply reforms it's reactants.
-3.10		The hydrogen molecule begins to vibrate and the system approaches the transition state, however there isn't enough energy to over come this reaction barrier and the reaction thus simply reforms it's reactants. A barrier recrossing process occurs.
3.1		The hydrogen molecule begins to vibrate and the system approaches the transition state, however there isn't enough energy to over come this reaction barrier and the reaction thus simply reforms it's reactants. A barrier recrossing process occurs.
6.1		The hydrogen molecule begins to vibrate and the system approaches the transition state, however there isn't enough energy to over come this reaction barrier and the reaction thus simply reforms it's reactants.

From the table above, we can see that these particular reaction trajectories are unsuccessful. However at -2 and +2, the reaction begins to become more feasible as a barrier recrossing process occurs. At -1 and +1, the reaction trajectory enables the reactants to fully react to form the products ( HF + H). Following Polanyi's empirical rules, one can identify that the success of the reaction is evidently dependent on the momentum of the approaching fluorine atom. A lower momentum thus enables a lower activation energy, therefore less energy is required to surpass this boundary and enable the reaction. However, when the vibrational energy of the transition state is too high, this newly formed H-F bond can break and reform the initial reactants instead. When the hydrogen has a high vibrational energy, the individual hydrogen atom will be out of the vicinity of the newly formed HF bond and will thus not be able to reform, hence the reaction would successfully proceed.

Polanyi's empirical rules is based upon this fundamental idea that in an exothermic reaction (early transition state), the translational energy holds more significance than the vibrational energy. This idea has been underlying the argument above. The F + H-H reaction is exothermic ( an early transition state), therefore the translational energy of the approaching fluorine holds more significance than that of the vibrational energy for the diatomic hydrogen . Good! Check through my comments in the rest of the wiki.Mak214 (talk) 14:59, 24 May 2020 (BST)

Contour plot of the new reaction trajectory under new defined conditions.

At the same position, there's a slight increase in the momentum of p_FH to -1.6 g.mol-1.pm.fs-1, and a reduction of the overall energy of the system by reducing the momentum of p_HH to 0.2 g.mol-1.pm.fs-1. These new conditions have enabled the reaction to proceed to form its products.

Contour plot of the new reaction trajectory under new defined conditions.

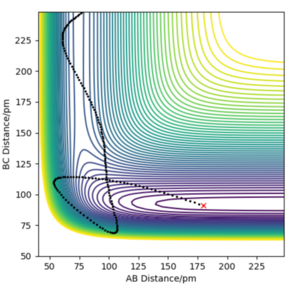
By decreasing the momentum of the incoming H atom and increasing the energy of the H - F vibration, a successful trajectory was achieved via 200 pm and 91 pm ( where the momentum is -20 and -1 respectively)

---