Jw4116 Y2 inorg-comp
PART 1
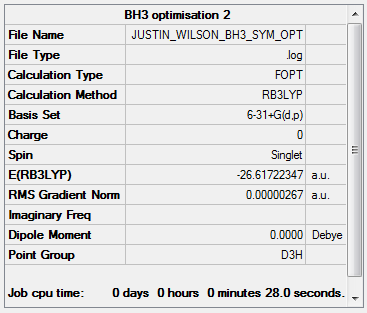
BH3
Calculation Method: RB3LYP
Basis Set: 6-31G(d,p)
Ng611 (talk) 18:30, 6 June 2018 (BST) Looks like your energy is off by a little bit for this molecule.
Item Value Threshold Converged? Maximum Force 0.000009 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000034 0.001800 YES RMS Displacement 0.000017 0.001200 YES Predicted change in Energy=-4.343399D-10
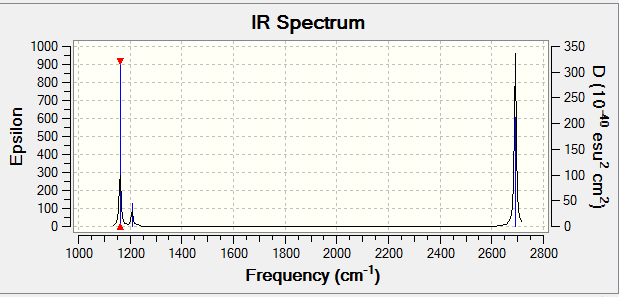
Frequency analysis log file .LOG file
Low frequencies --- -2.2126 -1.0751 -0.0054 2.2359 10.2633 10.3194 Low frequencies --- 1162.9860 1213.1757 1213.1784
Frequency Optimized BH3 |
| Mode | Symmetry | Frequency (± 100cm-1) | Intensity
ǃMode | |
|---|---|---|---|---|
| 1 | A2 | 1163 | 93 | out-of-plane bend |
| 2, 3 | x2 E' | 1213 | 14 | bend |
| 4 | A1' | 2582 | 0 | symmetric stretch |
| 5, 6 | x2 E' | 2715 | 126 | aymmetric stretch |
There are two reasons for the lack of 6 peaks in the IR spectrum, despite the number of modes calculated. The E' degenerate vibrational modes (2, 3 and 5, 6) absorb at the same frequency and hence cause the spectral peak to appear twice as large as the predicted intensity for 1 absorption. The other vibration (4) does not appears as it is IR inactive, symmetric and generates no dipole moment which is means it is unable to interact with the oscillating electric field.
MO diagram source [1]
Ng611 (talk) 18:33, 6 June 2018 (BST) Good MO diagram but you're missing computed orbitals for the 2e' level. You should also think about any similarities/differences between the real and computed MOs and reflect on the validity of qualitative MO theory.
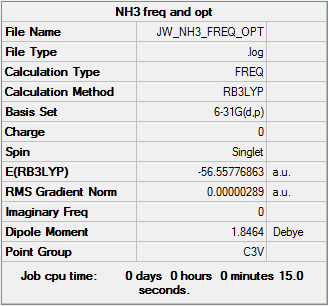
NH3
Calculation Method: RB3LYP
Basis Set: 6-31G(d,p)
Item Value Threshold Converged? Maximum Force 0.000005 0.000450 YES RMS Force 0.000003 0.000300 YES Maximum Displacement 0.000010 0.001800 YES RMS Displacement 0.000007 0.001200 YES Predicted change in Energy=-7.830784D-11
Frequency analysis log file .LOG file
Low frequencies --- -11.5222 -11.4865 -0.0028 0.0246 0.1415 25.6160 Low frequencies --- 1089.6618 1694.1735 1694.1738
Frequency Optimized NH3 |
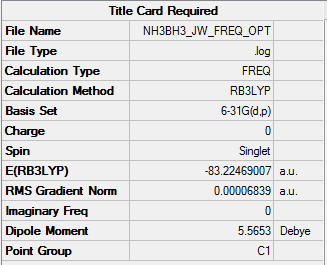
H3BNH3
Calculation Method: RB3LYP
Basis Set: 6-31G(d,p)
Item Value Threshold Converged? Maximum Force 0.000139 0.000450 YES RMS Force 0.000063 0.000300 YES Maximum Displacement 0.000771 0.001800 YES RMS Displacement 0.000338 0.001200 YES Predicted change in Energy=-2.028053D-07
Frequency analysis log file .LOG file
Low frequencies --- 0.0007 0.0007 0.0011 19.0877 23.7564 42.9908 Low frequencies --- 266.5949 632.3813 639.5072
Frequency Optimized H3NBH3 |
H3NBH3 Lewis Acid/Base B-N Bond Analysis
E(BH3)ː -26.61532363 au
Ng611 (talk) 18:35, 6 June 2018 (BST) From looking at your summary table for BH3, I can't see where you got this value from. Did you run a second calculation?
E(NH3)ː -56.55776863 au
E(H3NBH3)ː -83.22469007 au
ΔEformation(H3NBH3)ː -0.05159781 au = -135.47 kJ.mol-1 = -ΔEdissociation
Ng611 (talk) 18:38, 6 June 2018 (BST) Correct answer, but the final value should be reported to the nearest kj/mol
Analysisː The bond energy value calculated is in the rough ballpark for normal bond energies (b.t.w 200-500kJ.mol-1) however, as it is a dative bond formed from a Lewis acid/base pair it will be weaker (lower energy) than a traditional covalent bond in which an electron is donated by each atom. This logic correlates with the value calculated.
Ng611 (talk) 18:38, 6 June 2018 (BST) How does this bond strength compare with that of other bonds? Also, remember to cite your bond values (ideally from a textbook, databook, or paper).
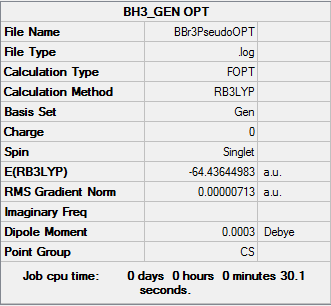
BBr3
Calculation Method: RB3LYP
Basis Set: 6-31G(d,p)LANL2DZ
Item Value Threshold Converged? Maximum Force 0.000015 0.000450 YES RMS Force 0.000006 0.000300 YES Maximum Displacement 0.000066 0.001800 YES RMS Displacement 0.000039 0.001200 YES Predicted change in Energy=-8.610617D-10
BBr3 .LOG file
Ng611 (talk) 18:41, 6 June 2018 (BST) You're missing the low-frequency modes here. Also, there needs to be a DSpace link in this section. The calculation looks correct, however.
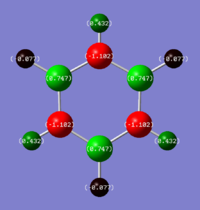
BBr3 |
PART 2
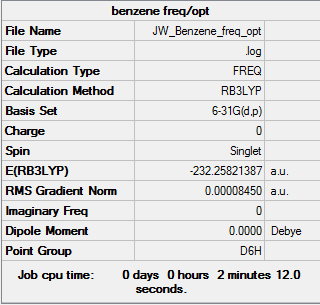
Benzene
Item Value Threshold Converged? Maximum Force 0.000199 0.000450 YES RMS Force 0.000081 0.000300 YES Maximum Displacement 0.000847 0.001800 YES RMS Displacement 0.000299 0.001200 YES Predicted change in Energy=-4.636845D-07
Benzene .LOG file
Benzene |
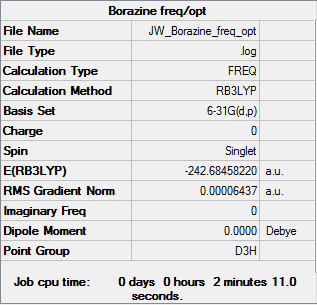
Borazine
Item Value Threshold Converged? Maximum Force 0.000086 0.000450 YES RMS Force 0.000033 0.000300 YES Maximum Displacement 0.000251 0.001800 YES RMS Displacement 0.000075 0.001200 YES Predicted change in Energy=-9.359581D-08
Borazine .LOG file
Borazine |
Charge Analysis
| Charge Distribution | Atom (Pauling E.N)ː Gaussian Value | Explanation |
|---|---|---|
|
N (3.04)ː -1.102
B (2.04)ː 0.747 H-N (2.20)ː 0.432/ H-B (2.20)ː -0.077 |
As shown in the picture and from general intuition from the knowledge of relative electronegativites, the charge distribution in borazine is very uneven. This is due to different hetero atoms having a exposed positive charge from the nucleus, increasing their ability to attract electron density from those atoms with a looser hold on their electrons. Although there is an uneven distribution of charge within the molecule, due to the symmetric distribution in charge, the molecule remains neutral with no single molecular dipole moment (they cancel out). The uneven distribution also results in a more reactive aromatic species as charges can attract nucleo/electrophillic species increasing the probability of a reaction (Nː nucleophillic, Bː electrophillic). Also half the protons would be more acidic than the other half based on their affinity to negative charge. |
|
C (2.55)ː -0.239
H-C (2.20)ː 0.239 |
Due to the higher symmetry of the benzene molecule (lack of heteroatoms) the charge distribution is even between each atom (H and C). As shown in the picture, the amount of charge on each atom is determined by their relative electronegativity and ability to attract electron density from the covalent bond. The symmetrical and even distribution in charge results in a very stable aromatic compound; however, the increased negative charge around the carbon atoms increases its imperceptibility to attack from strong electrophiles (seen in experiments). |
Ng611 (talk) 18:43, 6 June 2018 (BST) Good charge analysis. I'd perhaps add more detail regarding the symmetries of the molecule to strengthen this section further.
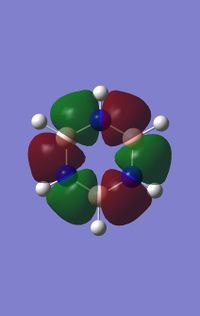
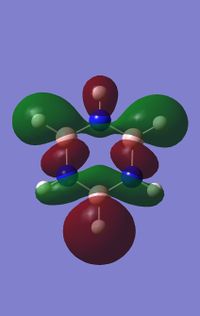
Comparing MOs
| Benzene MO (no.) | Borazine MO (no.) | Comparison |
|---|---|---|
|
|
These MOs are very similar in shape and nodal/ phase distribution. Due to the relative electronegativity, there is a slight distortion of electron density towards the nitrogen. However, due to the σ-nature of the MO, the distortion is much less due to the effectiveness of the overlap and rigidity of the MO. The contributing p-orbitals all lie in the same plane, perpendicular to the principle axis. |
|
|
As with MO14/15 the shapes of these MOs are very similar with the same nodal/ phase distribution and roughly the same shape. The difference in electronegativity and distribution of electron density is demonstrated by the reduction in symmetry from Benzene (D6h) to Borazine (D3h) as the electrons favour the N atom. This is a much more significant effect than the previous MO comparison due to the relative high diffusivity of π orbitals compared to σ. |
|
|
These wacky looking orbitals are also very similar but, like the other examples, have varied symmetry due to the distortion in electron density from the polarized bonds in the heteroaromatic ring. The effects of being bonded to electronegative atoms is seen in the contributions from the H1s orbitals to the MO. The hydrogens bonded to the nitrogen contribute significantly lower to the overall structure relative to those bonded to the boron atoms. |
Ng611 (talk) 18:48, 6 June 2018 (BST) Some good points made in this MO analysis, although they're somewhat inconsistently applied. As a minimum: for every orbital you compare you should consider the overall character of the orbital (sigma, pi etc) and the symmetry label of the orbital, relative contributions from AOs (and why the relative values are the way they are), how the symmetry/point group of the molecules affects the shapes of the orbitals, and the constituent AOs (i.e. 2px/y/z, 1s, etc.). You've done different bits for each orbital comparison, but not all of them for every orbital.
Aromaticity
Aromaticity is a very important concept in chemistry which relates to cyclic molecules and electron delocalisation. Aromatic compounds tend to be much less reactive than their more saturated counterparts due to the inherent stability associated with even electron distribution and delocalisation. A pioneer in the field of aromaticity was Hückel who devised a system/set of rules which determines the aromatic nature of a vast number of molecules. The rules require the molecule to have: 4n+2 π-electrons, be planar and have a connected system of delocalised p-orbitals along the principle axis of the molecule (perpendicular to the plane of the molecule). The classic aromatic molecule is benzene and its aromatic nature was first considered when the enthalpy of hydrogenation of poly-saturated cyclic hydrocarbons was studied; this confirmed that benzene was far more stable than expected which lead to the introduction of aromatic theory which was backed up by IR analysis. The effect of delocalisation and resulting ring current is seen in 1HNMR due to the induced magnetic field generated by the electrons whizzing around the pi system.
Nowadays, due to our more advanced analytical techniques, we have confirmed that a planar molecule with a system of delocalised electrons in a π MO is not a complete picture in describing the full extent/ nature and possible contributions leading to aromatic properties. One example would be the influence of σ-delocalised MOs (as seen in MO 14/15 above) which arises from the p-orbitals lying along the plane of the molecule. The electrons in this MO are clearly delocalised due to the nodal planes dissecting the nuclei rather than being inbetween them. The resulting MO is also lower in energy (more stable) than the π delocalised orbital due to the more effective σ overlap.[2] Other examples of aromatic compounds that break Hückels rules exist which display delocalised electrons and aromatic properties such as saturated inorganic rings (SiH2)n and (GeH2)n and a variety of others molecules.[3]
Ng611 (talk) 18:51, 6 June 2018 (BST) An interesting second paragraph. You mention σ-aromaticity -- what are some other modern examples of aromaticity? You also mention some key experimental indicators for aromaticity, are there any results in the literature for benzene/borazine that would allow you to contrast the aromatic nature of these two species?
Ng611 (talk) 18:54, 6 June 2018 (BST) This is a good report, although a number of missing bits throughout the report brought your grade down somewhat. Reading the script carefully and making use of the immediate feedback sessions on Friday to check that any key data is missing would have strengthened this report significantly. As it stands though, some good discussion and explanation here.
- ↑ http://www.huntresearchgroup.org.uk/teaching/teaching_comp_lab_year2a/Tut_MO_diagram_BH3.pdf
- ↑ Kovačević, Borislav, et al. "The origin of aromaticity: Important role of the sigma framework in benzene." ChemPhysChem 5.9 (2004): 1352-1364.
- ↑ Li, Zhen-Hua, et al. "σ-aromaticity and σ-antiaromaticity in saturated inorganic rings." The Journal of Physical Chemistry A 109.16 (2005): 3711-3716.