Jp3915Y2
EXERCISE 1: H + H2 system
The three hydrogen atoms are assigned for the following exercise in this section as shown in figure 1, with atom B and C as the original hydrogen molecule and atom A as a single atom.
Q1: What value does the total gradient of the potential energy surface have at a minimum and at a transition structure? Briefly explain how minima and transition structures can be distinguished using the curvature of the potential energy surface.
A1: The gradient is zero at the minimum and at the transition structure because they are stationary points. Curvature, i.e. second derivative, can be used to determine whether a stationary point is a minima or a maxima. Minima has a positive curvature and transition structure, which is a maxima, has a negative curvature.
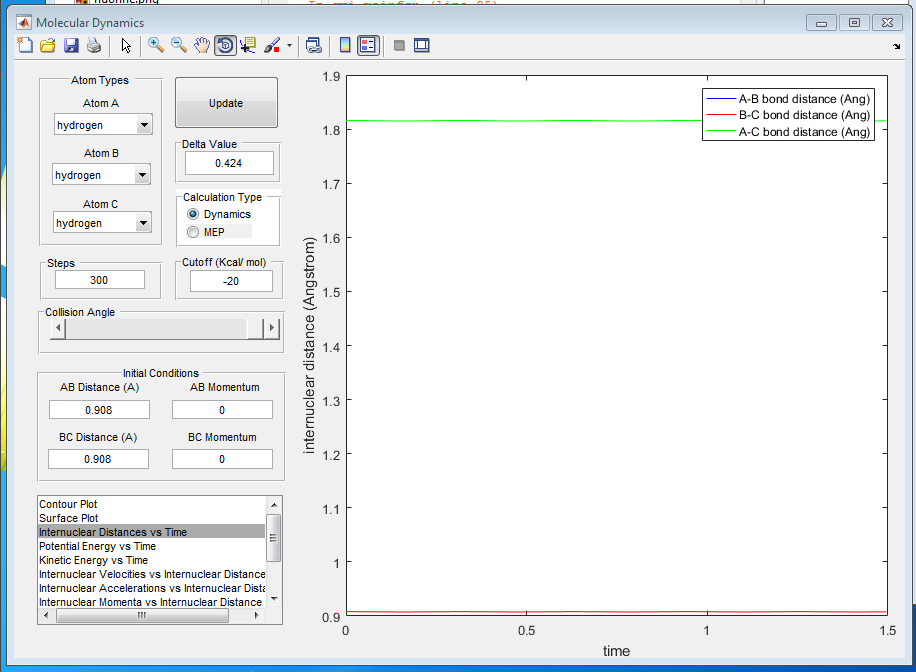
Q2: Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” screenshot for a relevant trajectory.
A2: The best estimate of the transition state position is measured to be 0.908Å. At this distance atom A and C are stationary and they will not be vibrating symmetrically about atom B. Internuclear distance vs time graph will be a horizontal straight line. The gradient dV/dr at transition state is zero, which indicates that the force on every atom is zero. Therefore the atoms stay stationary.
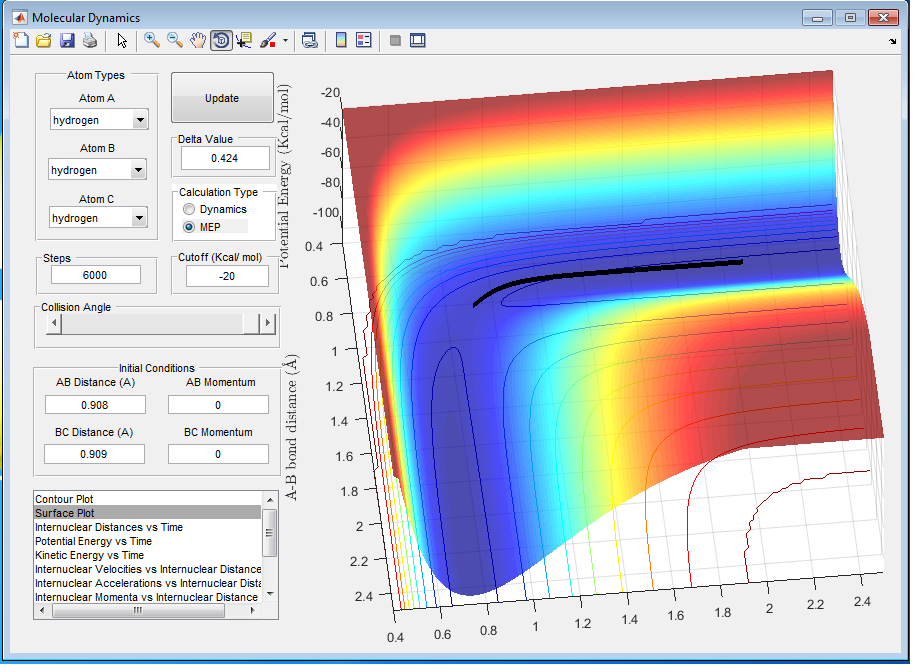
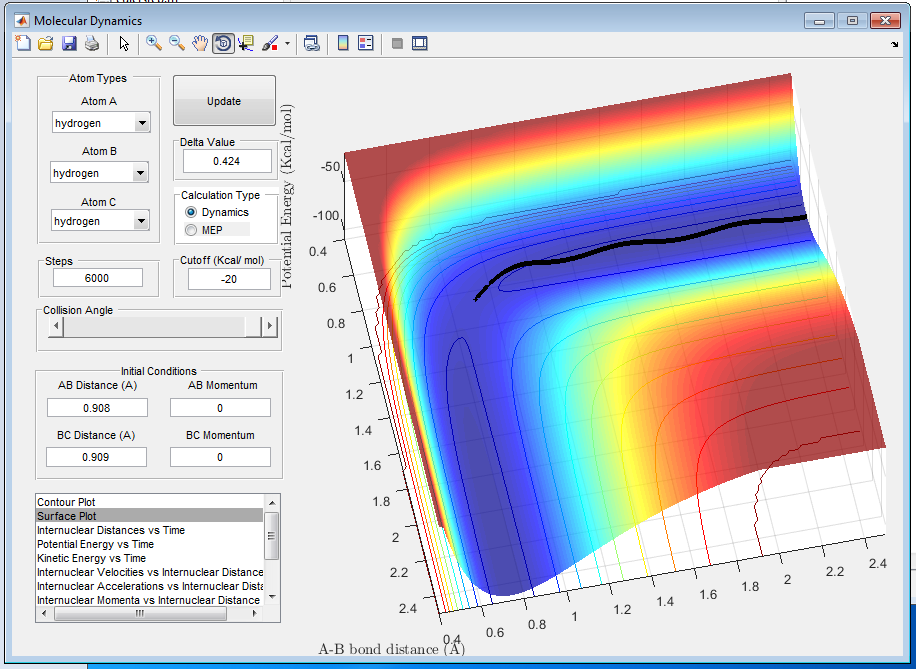
Q3: Comment on how the mep and the trajectory you just calculated differ.
A3: MEP describes the motion with the assumption that the atoms are not vibrating while Dynamics Calculation models the trajectory of vibrating atoms, which simulates actual chemical reactions better. As it is shown in figure 3, MEP trajectory follows the minimum energy path and it is a flat line. On the other hand Dynamics trajectory is wavy showing the motion of the vibrating atoms, as it is shown in figure 4.
Q4: Complete the table by adding a column reporting if the trajectory is reactive or unreactive. For each set of initial conditions, provide a screenshot of the trajectory and a small description for what happens along the trajectory.
A4:
| p1 | p2 | Result |
|---|---|---|
| -1.25 | -2.5 | reactive |
| -1.5 | -2.0 | unreactive |
| -1.5 | -2.5 | reactive |
| -2.5 | -5.0 | unreactive |
| -2.5 | -5.2 | reactive |
When p1=-1.25 and p2=-2.5 as shown in figure 5, reaction is completed and product is formed because there is enough energy to overcome the energy barrier. A-B vibrates more than B-C.

When p1=-1.5 and p2=-2.0 as shown in figure 6, reaction can not proceed because p2 is too small and there is not enough energy to reach the transition state. Atom A comes in vibrating, but it does not have enough momentum to react with molecule B-C. Then atom A vibrates away leaving molecule B-C unreacted.
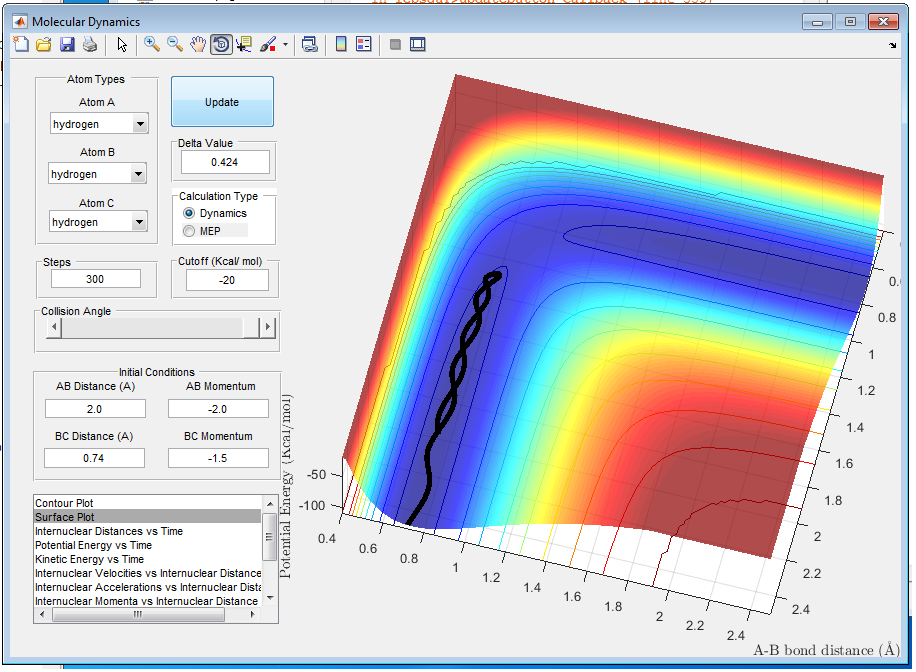
When p1=-1.5 and p2=-2.5 as shown in figure 7, reaction is completed and product is formed because there is enough energy to overcome the energy barrier. A-B vibrates more than B-C.
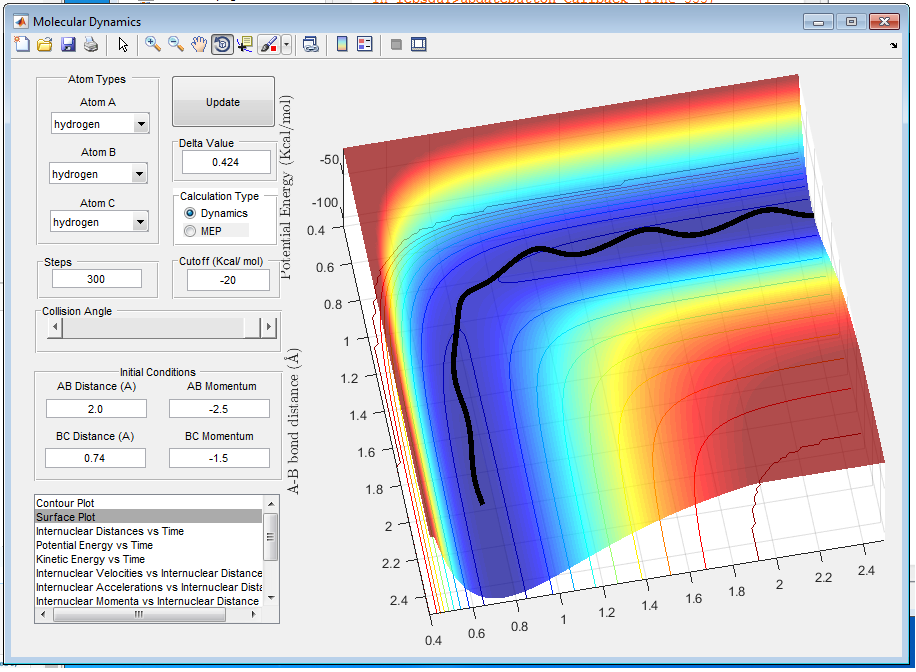
When p1=-2.5 and p2=-5.0 as shown in figure 8, p2 is big and there is enough energy to overcome the energy barrier. However the energy is too big and reaction can not proceed even though transition state is reached. In the animation, it can be seen that bond B-C breaks while colliding with atom A and bond A-B is formed. Then atom C vibrates back in, colliding with the newly formed molecule AB with great kinetic energy, which leads to the breaking of bond A-B and reforming of bond B-C.

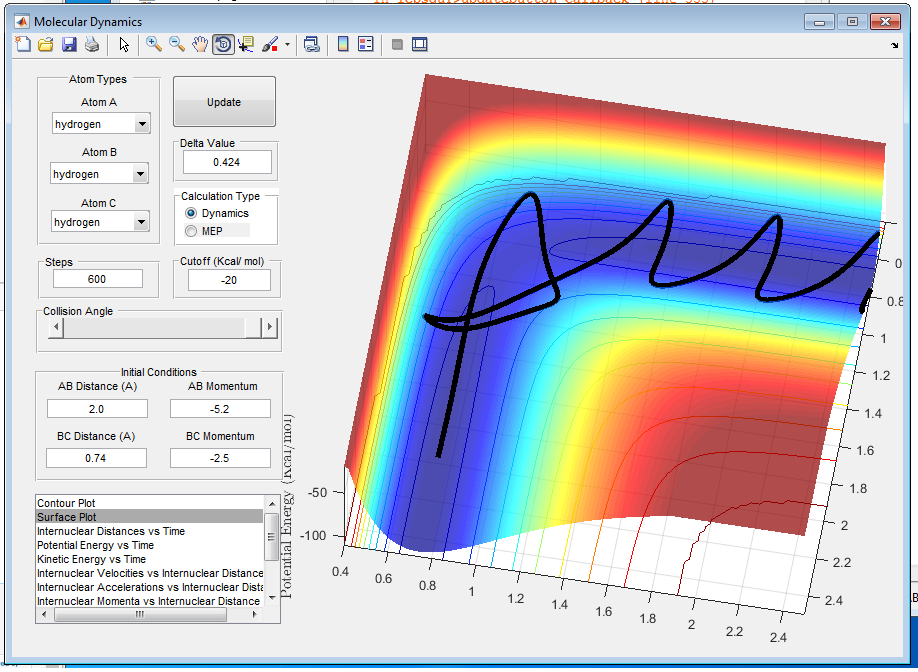
When p1=-2.5 and p2=-5.2 as shown in figure 9, there is enough energy to overcome the energy barrier and transition state is reached. Comparing with the fourth case it could be seen that reaction with a lot of energy applied is quite unpredictable and it will not always proceed to foerm the product.
Q5: State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?
A5: TST assumes that atomic nuclei behave classically. There is no particle tunneling through the energy barrier. And reaction will proceed as long as the particles collide with enough energy and transition state is reached[1]. In reality, there are probabilities that particles can tunnel through energy barrier so reaction rate measured experimentally is higher than the TST prediction. Moreover, TST ignores factors other than energy that can also determine whether the reaction can happen or not. Comparing the fourth and fifth case in Q4 it can be seen that colliding with more energy does not guarantee that reactions will happen. Colliding with the correct vibrational mode so that the excess kinetic energy will not break the newly formed bond is also important.
EXERCISE 2: F - H - H system
Q6: Classify the F + H2 and H + HF reactions according to their reaction energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?
A6: As it is shown in the figure 10, the product channel is lower in energy than the reactant channel, so F + H2 is an exothermic reaction. In figure 11, the product channel is higher in energy than the reactant channel, therefore H + HF is an endothermic reaction. This indicates that H-F bond is stronger than H-H bond because energy needed to break the H-F bond is more than the energy given out when H-H bond is formed. This can also be verified by the fact that bond energy of H-H bond is lower than that of H-F[2].

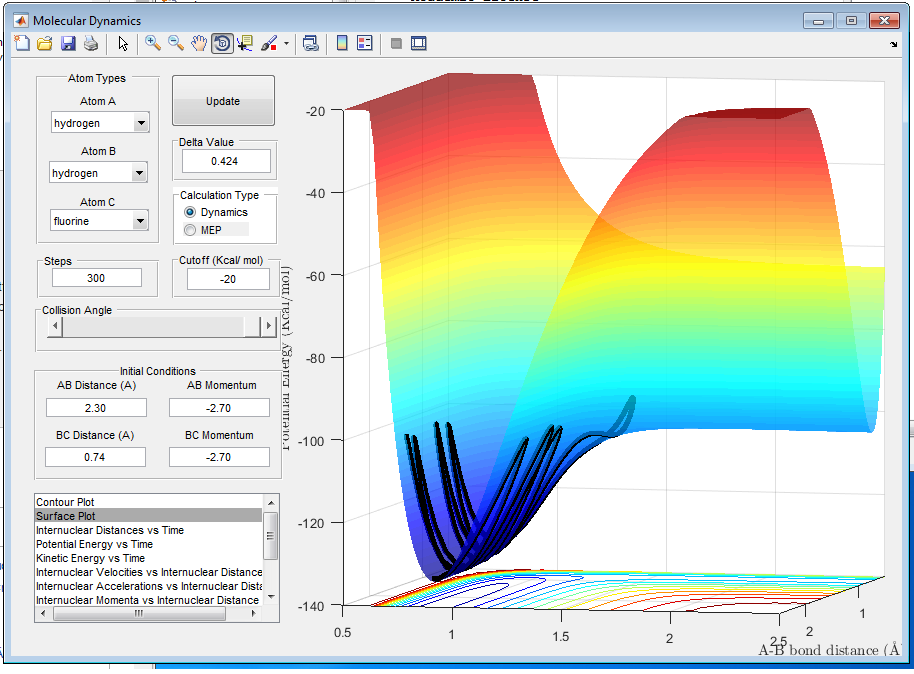
Q7: Locate the approximate position of the transition state.
A7: The Hammond's Postulate states that in an exothermic reaction the transition state is closer in energy to the reactant than to the product so the transition state will be more geometrically similar to the reactant than to the product[3]. So for the exothermic reaction F + H2, the transition state can be found in the reactant channel. The transition state position is found to be r1 = 0.750Å and r2 = 1.801Å. The Internuclear Distance vs Time graph of this state is three horizontal lines with a little oscillation.
Q8: Report the activation energy for both reactions.
A8: The activation energy of H + HF is calculated to be 30.1 Kcal/mol as shown in figure 12 and 13, using the energy difference on the potential energy vs time graph. By offsetting the fluorine atom a little bit further away from transition state, the activation energy of F + H2 is calculated to be 0.2 Kcal/mol as shown in figure 12 and 14.
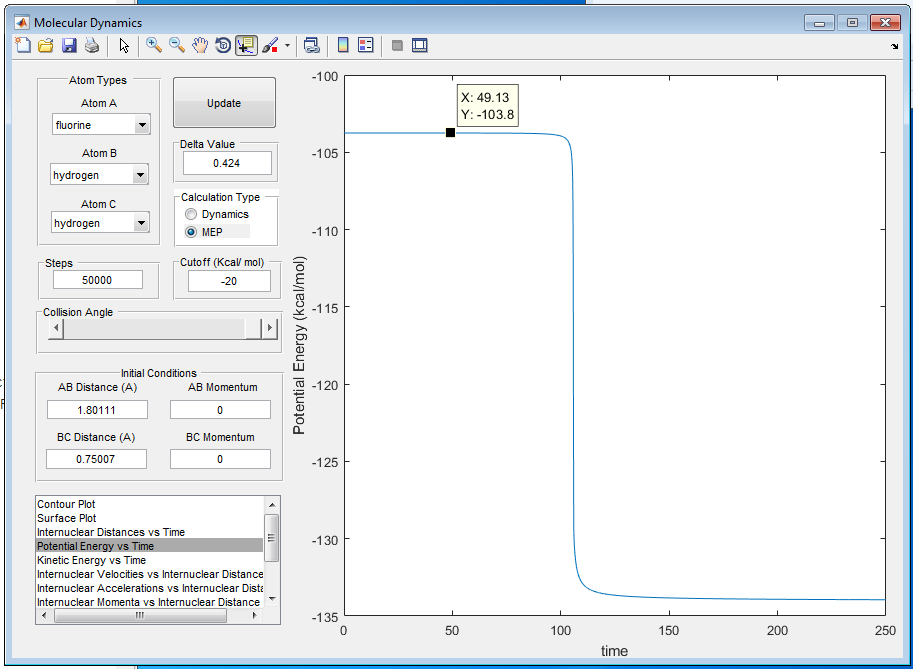
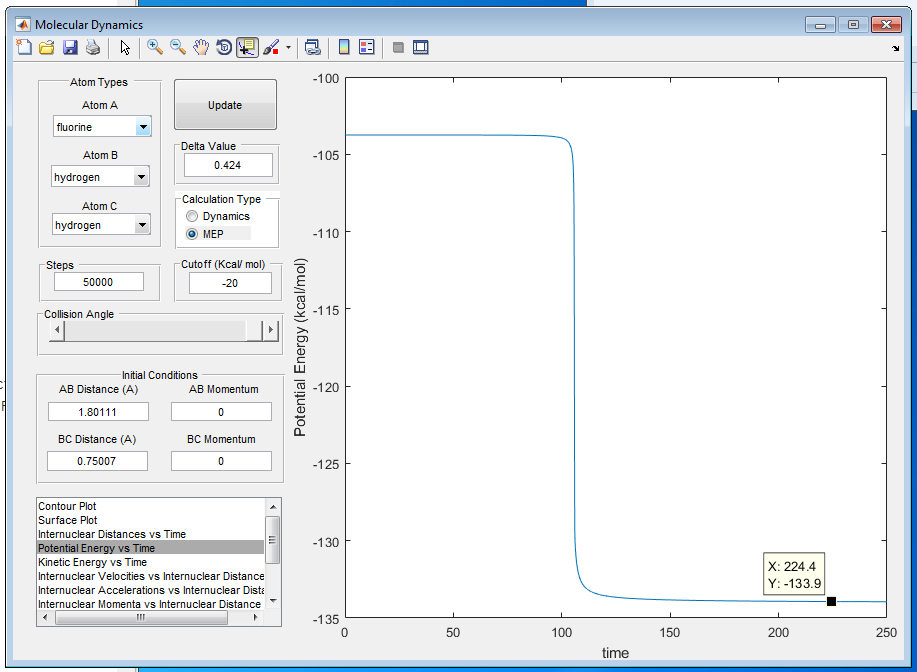
Q9: In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. How could this be confirmed experimentally?
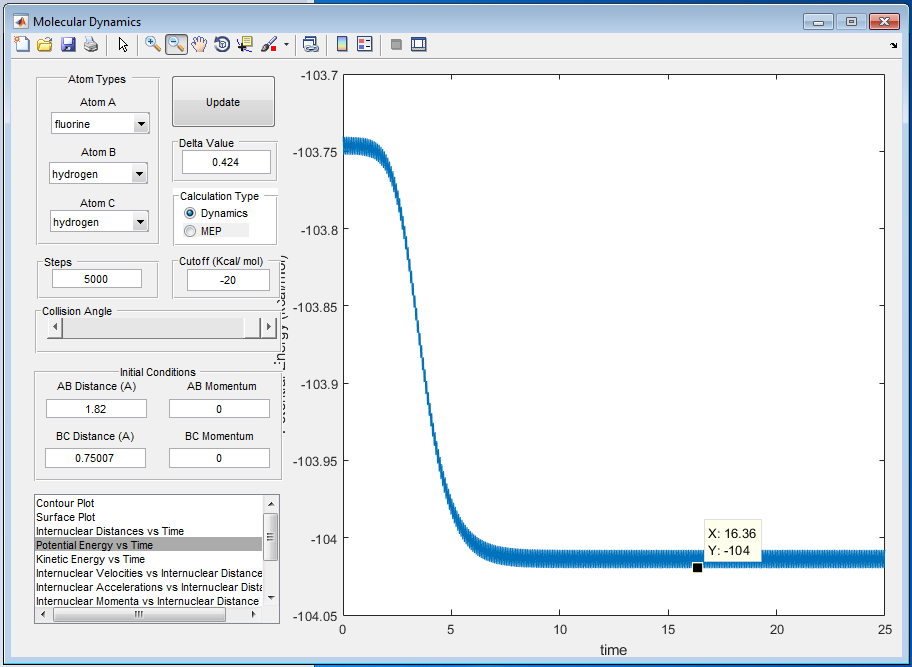
A9: The incoming F atom collides with the H-H molecule and the translational energy of F atom is converted into the vibrational energy of the H-H bond, causing it to break. F + H2 is an exothermic reaction and potential energy decreases as a result. Energy is conserved and energy released will then be converted into vibrational energy of H-F bond and translational energy of the leaving H atom. It can be seen from figure 16 that the new H-F bond vibrates more than the original H-H bond because of the extra vibrational energy gained. Calorimetry can be used to confirmed this mechanism where energy giving out can be measured over time.
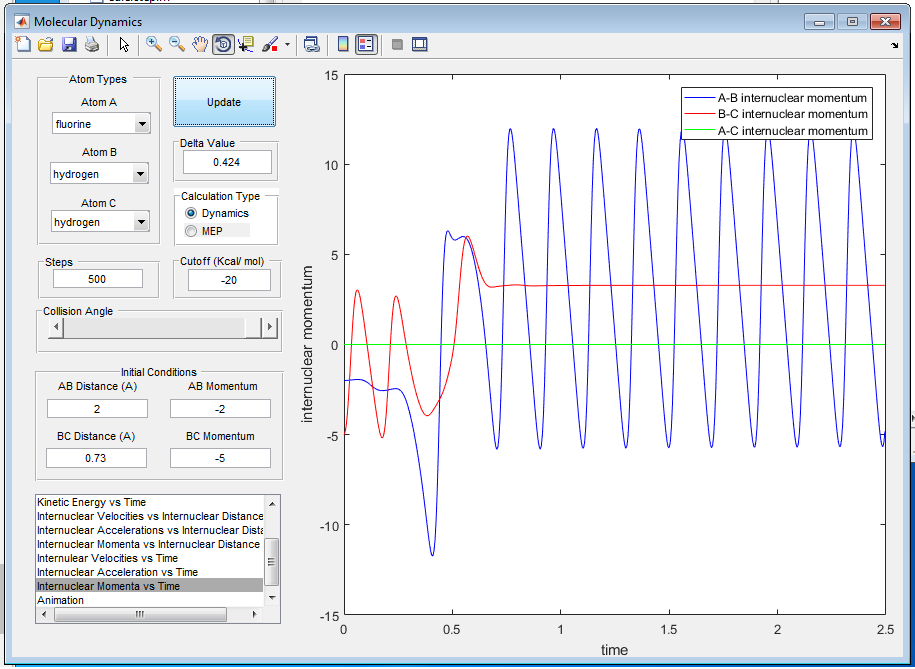
Q10: Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.
A10: The Polanyi rules state that vibrational energy is more efficient in promoting a late-barrier reaction, i.e. an endothermic reaction where the transition state is closer in energy to the products than reactants, than translational energy. In contrast, translational energy is better at promoting an early-barrier reaction, i.e. an exothermic reaction, than vibrational energy[4]. For example, H + HF is an endothermic reaction so the greater momentum H-F has, the more likely the reaction is going to occur. Vibrational energy and translational energy should be in the right ratio for maximum efficiency of the reaction.
Reference
[1] Truhlar, D. G., Garrett, B. C., Klippenstein. S, J. Phys. Chem. 100 (31): 12771–12800.
[2] John A. Dean, Lange's Handbook of Chemistry, Sixteenth Edition, McGraw-Hill INC, USA, 1999.
[3] Carey, Francis A., Sundberg, Richard J, Advanced Organic Chemistry, Part A: Structure and Mechanisms, Springer, USA, 2007.
[4] Zhaojun Zhang, Yong Zhou, and Dong H. Zhang, J. Phys. Chem. Lett., 2012, 3 (23), pp 3416–3419.
