Molecular Reaction dynamic

Introduction

This wiki page introduce a method to find the how the translational energy and vibrational energy affect the reaction trajectory in order to give the best combination for starting a reaction. The reaction trajectory are calculated and modelled by MATLAB. Two triatomic reactions are going to be discussed.

H + H₁ system

Hydrogen atom A attacks hydrogen molecule BC, A forms molecule with B and C is pushed away.

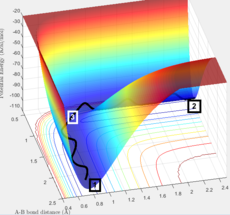
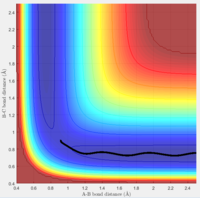
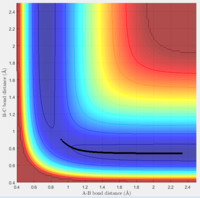
Figure 1 is the potential energy surface of the above reaction. The reaction starts from the point 1, end in point 2, point 3 is at the area where the transition state (TS) located.

Both the gradients of the potential energy surface of transition state and the minima are 0. Therefore, the total gradient is 0.

Figure 2. view in the surface of potential energy against bond distances

Figure 3. in the surface of PE against A-B bond

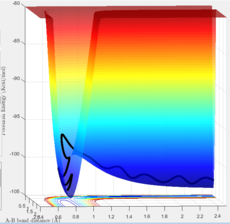
To distinguish them, the potential energy surface curve need to be viewed in 3D. In the surface of potential energy against bond distances (Figure 2), the second derivative of the curve at transition state is smaller than 0. Whereas when viewing the graph in the surface of PE against A-B bond distance (Figure 3), the second derivative of the curve at the same point becomes to be larger than 0. On the other hand, for the minima of the graph, the second derivative of the curve at that point is always larger than 0.

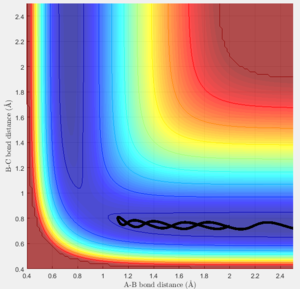
The best estimate position for the transitional state is r_ts = 0.908 ang. 2 almost straight line appear on the Internuclear Distances vs Time graph (Figure 4).

At transition state, the potential energy is at its maximum.

When there is no fluctuation in the internuclear distance (i.e. constant distance between A, B and C) as time process, the 3 H atoms reach equilibrium, which means there is nearly no kinetic energy among them, thus, the potential energy is maximum. So the best estimate TS position is 0.908 ang.

Reaction trajectory at the almost TS position

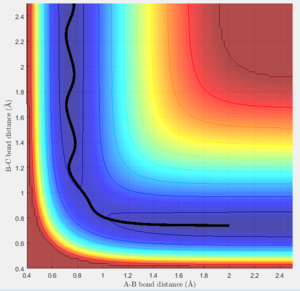
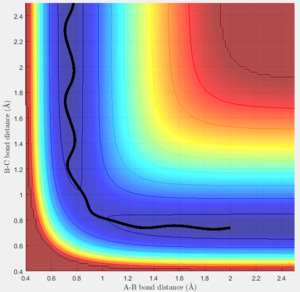
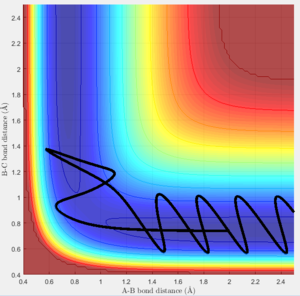
Both the dynamic calculation and minimum energy path (mep) calculation were used in order to find the reaction path when the position is slight removed away from the transitional state position.

The MEP gives a perfect straight line from TS to the product while the dynamic calculation provides a wavy line. Because the MEP calculation always takes the minimum energy points, so it is a straight line. However, for the dynamic calculation, it accounts the natural oscillation of the newly formed AB molecule, therefore, it is a wavy line. (Figure 5)

Table 1 and 2 show the dynamic calculation of the H + H₂ reaction starting at a point slightly away from the TS position. In table 1, the starting material is BC molecule and A atom, after changing the initial condition (table 2), it becomes AB molecule and C atom. The initial positions are all same, so the product at the same finish time have the same conditions.

At 3.145 time, the A-B and B-C have the same intramolecular distance and no momentum. The distance of A-C is 1.825 Ang and 0 momentum. This can indicate that 3Hs reach an equilibrium and returns to the transition state. (A reverse process from reactants back to transition state position)

Figure 5 (top) dynamic calculation, (bottom) MEP calculation.

Table 1	Internuclear distance (Ang)	Internuclear momentum
B-C (t=0)	0.908	0
A-B (t=0)	0.918	0
B-C(t=3.145)	0.7247	1.137
A-B(t=3.145)	11.43	2.481

Table 2	Internuclear distance (Ang)	Internuclear momentum
B-C (t=0)	0.918	0
A-B (t=0)	0.908	0
B-C (t=3.145)	11.43	2.481
A-B (t=3.145)	0.7247	1.137

**Table 3**
t=0	Internuclear distance (Ang)	Internuclear momentum	t=3.145	Internuclear distance (Ang)	Internuclear momentum
A-B	11.43	-2.481	A-B	0.9106	0
B-C	0.7247	-1.137	B-C	0.9106	0

Will a higher KE cross the activational barrier easier and start the reaction faster ?

The initial position is set to be rBC =0.74 Ang and rAB=2 Ang (i.e a BC molecule and an A atom). Several trajectories were run with different momentum combinations to test if reactions are reactive (R) or unreactive (U) with these combinations.

P_BC	P_AB	Reactive?	Trajectory
-1.25	-2.5	R	a
-1.5	-2.0	U	b
-1.5	-2.5	R	c
-2.5	-5.0	U	d
-2.5	-5.2	R	e

a. A approaches B steadily, they form a AB molecule and push C away from B. C becomes an atom.	b. A approaches B slowly, the kinetic energy is not enough to overcome the activation barrier, therefore, no new molecule form, the BC molecule and the A atom remain the same.
c. A approaches B with a rate faster than in trajectory b, the KE is enough to overcome the barrier to form AB and push C away.	d. A approaches BC with an even faster rate but BC has an increased velocity this time, the KE difference between AB and C is may be large enough to overcome the activation barrier, however it has not reach the ‘escape rate’. Therefore, several recrosses happened and return back to reactants.	e. A approaches BC with a faster velocity, the KE difference is able to overcome the activation gap to form a molecule AB with high amplitude vibration while pushing C away gradually.

Relating with transition state theory

The TS theory assumes that there is enough energy for a system to stay in the transition state, and once the system pass the TS position, it will immediately and definitely falling into the product area and form products. The trajectory should only fall to the product side and would not recross or go back to the reactant side.

This is not true for the reality, as the reacting components can be affected by the environment such as the solvent molecules, the other reacting molecules etc.

This means that the TS theory also assumes that there is an isolating degree of freedom of each component, they will not affect by each other.

Due to the difference of the TS theory and the reality, the rate predicts by the TS theory will always be greater than the actual reaction rate.

H₂ + F and HF + H systems

For the reaction F + H₂, the transition position for BC is 0.748Ang and for AB is 1.809Ang.

Figure 6 surface graph of the H₂ +F reaction.	Figure 7 potential energy vs time graph

From the surface graph (Figure 6), it can be seen the reaction is exothermic as the reactants have higher PE than the products. According to the Hammond postulate, the exothermic reaction has early TS which means the TS is closer to the reactants than the products. By trying the positions located in the reactants area, the optimum value is found for the transition state position. The activation energy is about 0.27Kcal/mol using the dynamic calculation (Figure 7). Since the energy is too small, energy change happen in a very short time, the graph of MEP calculation is not too useful to see the change

Figure 8 surface graph of the HF + H reaction	Figure 9 PE vs time graph

For the H + HF reaction, (Figure 8) since it is an endothermic reaction, the TS position is closer to the products, which is F + H2. Therefore, the TS position for H + HF reaction is the same as the F + H2, which is BC = 0.749 Ang and AB = 1.809 Ang. The activation energy is about 30 Kcal/mol using the MEP calculation, this can be seen from the PE vs time graph (Figure 9).

Reaction Dynamics

Consider the reaction F + H₂ The initial position is set to be rHH(BC) = 0.74 Ang, rFH(AB) = 2 Ang and the AB momentum = -0.5

The BC momentum was changed between -3 to 3 by 0.1. It was found that the optimum range is from -1 to 0.5 for the reaction to be reactive. When the absolute value of BC momentum is greater than 1,there are less reactive reaction happens, the possibility for the reactive reaction to occur decreases. This can be due to the fact that the greater the absolute value of BC momentum, the greater vibrational energy there are in the system, the molecule will hit the potential wall harder, and the energy is strong and hard to control. The translational momentum (AB) compares to the vibrational momentum (BC) is too small, their overall momentum will be much closer to the BC direction then the AB direction. Therefore, the system keep vibrating in the reactant side when the system crosses the activation barrier to the product side it will soon recross the barrier back to the reactant side.

When the AB momentum is changed to -0.8 and the other conditions do not change. The optimum range of BC momentum for the reaction to occur becomes -1 to 1. This time, the translational momentum increases, the overall momentum will be closer to the AB direction therefore it is more likely for the reaction to cross the barrier and fall to the product side.

From above observation, it can be roughly concluded that a large translational energy and a small vibration energy are the suitable combination to let a reaction occur.

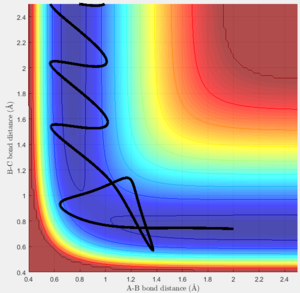
Now, the reaction HF + H is considered, AB distance = 0.74 Ang and BC distance = 2 Ang.

After many trials of different combination of AB and BC momentums under 10, there is no such a combination that can allow the reaction to occur. It is either the translational momentum is too small to overcome the barrier or the it is too large that the system bounces back to the reactant side (Figure 10).