Jessica 01335543
AMMONIA - NH3
Optimisation of NH3
Calculation Method: RB3LYP
The basis set: 6-31G(d.p)
The final energy E(RB£LYP): -56.55776873 au
The RMS gradient: 0.00000485 au
The point group of the molecule: C3V
Optimised N-H bond distance: 1.01798 Angstrom
Optimised H-N-H bond angle: 105.741 degrees
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000072 0.001800 YES
RMS Displacement 0.000035 0.001200 YES
Predicted change in Energy=-5.986254D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.018 -DE/DX = 0.0 !
! R2 R(1,3) 1.018 -DE/DX = 0.0 !
! R3 R(1,4) 1.018 -DE/DX = 0.0 !
! A1 A(2,1,3) 105.7412 -DE/DX = 0.0 !
! A2 A(2,1,4) 105.7412 -DE/DX = 0.0 !
! A3 A(3,1,4) 105.7412 -DE/DX = 0.0 !
! D1 D(2,1,4,3) -111.8571 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
Link to completed NH3 optimisation: Media:HJC3917_NH3_OPTF_POP.LOG
Jmol Dynamic Image of NH3
Ammonia |
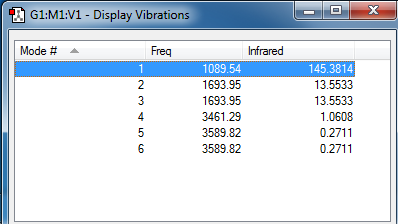
Molecular Vibrations of NH3
Electronic Charge Distributions of NH3
Analysis of NH3
How many modes were expected from the 3N-6 rule?
Since there are 4 atoms in NH3, six vibrational modes were expected.
Which modes are degenerate?
Modes 2 and 3, and 5 and 6 are degenerate as the same frequencies are observed.
which modes are "bending" vibrations and which are "bond stretch" vibrations? Modes 1, 2, and 3 are bending vibrations, whilst Modes 4, 5, and 6 are bond stretches.
which mode is highly symmetric? Mode 4 is highly symmetric as the symmetric stretch is observed.
Which mode is known as the "umbrella" mode?
Mode 1 is known as the "umbrella" mode, due to the appearance of the opening and closing of the "umbrella" upon stretching.
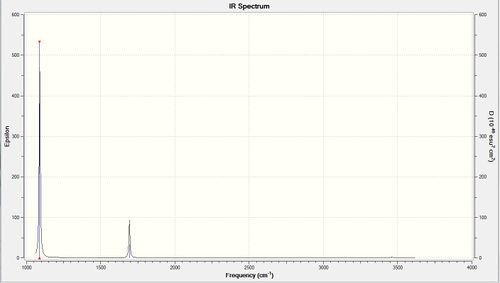
how many bands would you expect to see in an experimental spectrum of gaseous ammonia?
4 bands would be expected in the IR spectrum as the IR is absorbed at 4 different frequencies and thus four different wavenumbers.
However from the absorption spectrum only 2 main peaks are observed, namely Mode 1 and Mode 2 (degenerate with Mode 3) of intensities of 145.38 au and of 13.6 au respectively. Mode 1 is of a higher intensity due to the umbrella mode eluding to a larger change in dipole moment; Mode 2 has a less large change in dipole moment although there are two degenerate asymmetric stretches, hence the observation of a lower-intensity peak. However Modes 4, 5 and 6 lead to too small dipole moment changes: the intensities of the peaks are too low and would not be observed due to noise in the IR spectrum.
The charges of N and H are -1.125 and 0.375, respectively. N is more electronegative than H, so it follows that the charges displayed are in agreement with theory, ie that N has a negative charge and H has a positive one, as in the polar bond the electrons are pulled towards the N.
THE HABER-BOSCH PROCESS
NITROGEN - N2
Optimisation of N2
Calculation Method: RB3LYP
The basis set: 6-31G(d.p)
The final energy E(RB£LYP): -109.52412868 au
The RMS gradient: 0.00000100 au
The point group of the molecule: D∞H
Optimised N-N bond distance: 1.10550 Angstrom
Optimised H-N-H bond angle: 180 degrees
Item Value Threshold Converged?
Maximum Force 0.000002 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000001 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Predicted change in Energy=-9.478011D-13
Optimization completed.
-- Stationary point found.
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
Link to completed N2 optimisation: Media:HJC3917_N2_OPTF_POP.LOG
Jmol Dynamic Image of N2
Nitrogen |
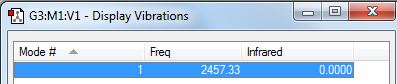
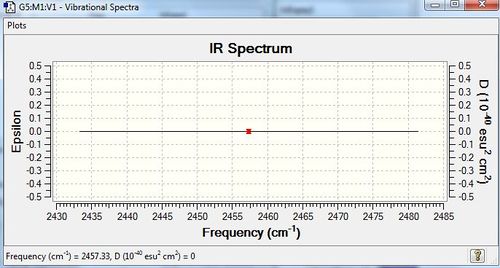
Molecular Vibrations of N2
Electronic Charge Distributions of N2
Analysis of N2
N2 should have, from the 3N-5 rule as it is linear, 1 mode. There is one stretching vibration, which is highly symmetric. Since this does not lead to a change in dipole, and since there is a charge distribution of zero as it is a homonuclear diatomic, no peaks would be observed in the IR spectrum; N2 is IR inactive.
N2 Molecular Orbitals of N2
In order of increasing energy

MO 1:σg bonding molecular orbital - made from the constructive overlap of the 1s atomic orbitals

MO 2:σ*u antibonding molecular orbital - made from the destructive overlap of the 1s atomic orbitals

MO 3:σg bonding molecular orbital - made from the constructive overlap of the 2s atomic orbitals

MO 4:σ*u antibonding molecular orbital - made from the constructive overlap of the 2s atomic orbitals

MO 5 and 6 (degenerate):πu bonding molecular orbital - made from the constructive overlap of the 2py or 2pz atomic orbitals
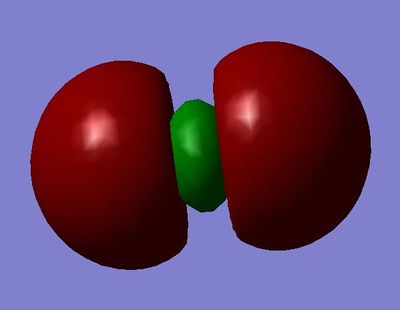
MO 7:σg bonding molecular orbital - made from the constructive overlap of the 2px atomic orbitals

MO 8 and 9 (degenerate):π*g antibonding molecular orbital - made from the destructive overlap of the 2py or 2pz atomic orbitals

MO 10:σ*u antibonding molecular orbital - made from the destructive overlap of the 2px atomic orbitals
The HOMO based on the molecular orbital theory is the 3σg, whilst the LUMO is the 2 π*g antibonding molecular orbital.
There is s-p mixing, as there are interactions between the molecular orbitals of the same symmetry. The expected order of molecular orbital energies thus changes so that the higher-energy π molecular orbitals are at a lower energy than the high energy σ molecular orbitals (formed from an amalgamation of both the 2s and 2p atomic orbitals) hence all of the molecular orbitals in N2 are either bonding or antibonding, as opposed to non-bonding. Since, in total, there are five bonding orbitals filled with a pair of electrons and two anti-bonding orbitals filled with a pair of electrons, the bond order between the two N atoms is thus 3; bond order = [(5*2-2*2)/2] = 3
HYDROGEN - H2
Optimisation of H2
Calculation Method: RB3LYP
The basis set: 6-31G(d.p)
The final energy E(RB£LYP): -1.17853936 au
The RMS gradient: 0.00000017 au
The point group of the molecule: D∞H
Optimised H-H bond distance: 0.74279 Angstrom
Optimised H-H bond angle: 180 degrees
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000001 0.001200 YES
Predicted change in Energy=-1.164080D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 0.7428 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
Link to completed H2 optimisation: Media:HJC3917_H2_OPTF_POP.LOG
Jmol Dynamic Range of H2
Hydrogen |
H2 Vibrations of H2
Electronic Charge Distributions of H2
Analysis of H2
H2 should have, from the 3N-5 rule as it is linear, 1 mode. There is one stretching vibration, which is highly symmetric. Since this does not lead to a change in dipole, and since there is a charge distribution of zero as it is a homonuclear diatomic, no peaks would be observed in the IR spectrum; N2 is IR inactive.
Reactivity and Energy Change Calculations
E(NH3)= -56.55776873 au
2*E(NH3)= -113.1155375 au
E(N2)= -109.52412868 au
E(H2)= -1.17853936 au
3*E(H2)= -3.53561808 au
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.05579074 au
Thus the exothermic energy change is: -146.48 kJ mol -1 (2 d.p.)
Since energy is released in the forward reaction, the ammonia product molecules are at a lower energy in comparison to the nitrogen and hydrogen reactants. Hence the products are more stable than reactants.
The Literature Value for the enthalpy change of formation is -92 kJ mol -1. [1]
A reason for this disparity could be due to the fact that both of the Haber Process conditions were different in both reactions. The less exothermic literature value indicates that, in reality, less energy is released to form the more stable ammonia product due to uncontrolled experimental factors.
SELECTED MOLECULE: CHLORINE - Cl2
Optimisation of Cl2
Calculation Method: RB3LYP
The basis set: 6-31G(d.p)
The final energy E(RB£LYP): -920.34987886 au
The RMS gradient: 0.00002510 au
The point group of the molecule: D∞h
Optimised N-H bond distance: 2.04174 Angstrom
Optimised H-N-H bond angle: 180 degrees
Item Value Threshold Converged?
Maximum Force 0.000043 0.000450 YES
RMS Force 0.000043 0.000300 YES
Maximum Displacement 0.000121 0.001800 YES
RMS Displacement 0.000172 0.001200 YES
Predicted change in Energy=-5.277245D-09
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 2.0417 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
Link to Completed Cl2 Optimisation: Media:HJC3917_CL2_OPTF_POP.LOG
Jmol Dynamic Range of Cl2
Chlorine |
Molecular Vibrations of Cl2
Electronic Charge Distributions of Cl2
Analysis of Cl2
From the 3N-5 rule, as Cl2 is a linear molecule, one vibrational mode was expected. There are no degenerate modes, as there is only one mode - a symmetric stretch. There are no bending vibrations, and since there is no change in dipole moment, the molecule cannot be detected in the IR spectrum hence no bands would be observed. Since the molecule is a homonuclear diatomic, there is no dipole and thus the charge distribution is zero, as demonstrated by the above image; Cl2 is IR inactive.
Molecular Orbitals of Cl2
The six selected orbitals are ordered in increasing energy.

Molecular Orbital 11: σg bonding molecular orbital made from the constructive overlap of 3s orbitals
Energy= -0.93313 kJ/mol

Molecular Orbital 12:σ*u anti-bonding molecular orbital made from the destructive overlap of 3s orbitals
Energy= -0.77746 kJ/mol

Molecular Orbital 13:σg bonding molecular orbital made from the constructive overlap of 3px orbitals
Energy= -0.47392 kJ/mol

Molecular Orbitals 14 and 15 (degenerate):πu bonding molecular orbital made from the constructive overlap of 3py or 3pz orbitals
Energy= -0.40695 kJ/mol
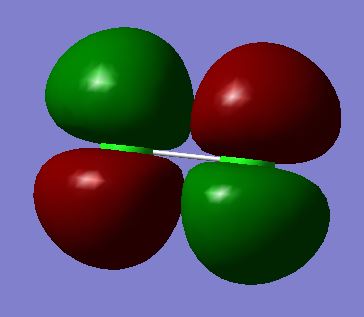
Molecular Orbitals 16 and 17 (degenerate): π*g anti-bonding molecular orbital made from the destructive overlap of 3py or 3pz orbitals
Energy= -0.31361 kJ/mol
This is the occupied HOMO, containing the valence electrons in the Cl2 molecule

Molecular Orbitals 18:σ*u anti-bonding molecular orbital made from the destructive overlap of 3px orbitals
Energy= -0.14206 kJ/mol
This is the LUMO (the only unoccupied orbital analysed here) in the Cl2 molecule
Analysis of Cl2
There is no s-p mixing, as there is no interaction between the molecular orbitals of the same symmetry. The expected order of molecular orbital energies remained the same (formed from an amalgamation of both the 2s and 2p atomic orbitals) hence all of the molecular orbitals in Cl2 are either bonding or antibonding.
In comparison to N2 (analysed in 2.1.6) the s orbitals in Cl2 possess more s character, as do the p orbitals, due to less s-p mixing. This is due to the fact that in this case, the s and p orbital gap is much larger, hence orbital mixing is significantly lower. This difference can be easily observed in the molecular orbital diagrams, for instance Molecular Orbital 13 in Cl2 clearly possesses only p character due to symmetry of the orbitals, nevertheless the s character influencing the molecular orbital of Molecular Orbital 7 in N2 is evident.
The filling of the bonding orbitals stabilise the molecule, whilst the filling of the antibonding orbitals destabilise it, so due to the higher proportion of bonding orbitals being filled in N2 principle alone, the N2 molecule is more stable. Of course, the presence of the triple bond significantly stabilises the molecule in comparison to the single bond in the chlorine molecule.
The Gaussview basis set used was 6-31 G(d,p), rendering all non-hydrogen s orbitals having p character, and all non-hydrogen p orbitals having d character. Thus there was more freedom in describing the molecular orbitals with greater nodality.
Since, in total, there are nine bonding orbitals filled with a pair of electrons and eight anti-bonding orbitals filled with a pair of electrons, the bond order between the two Cl atoms is thus one; bond order = [(9*2-8*2)/2] = 1
Bibliography and References
1. The Haber Process https://www.chemguide.co.uk/physical/equilibria/haber.html Date Accessed: 9th March 2018