Jc1506:copley02

BH₃ Introduction Molecule

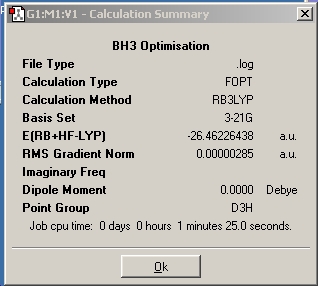
Firstly, BH₃ was drawn in the Gaussview window. By default, bond lengths were 1.18Å and bond angles were 120^o. From this, all bond lengths were set to 1.5Å. The molecule was then optimised using the DFT B3LYP method and 3-21G basis set for speedy and not particularly accurate optimisation. The calculation was submitted to Gaussian, and the output opened to reveal the optimised molecule.

The optimised B-H bond distance is 1.19Å H-B-H bond angle is 120.0^o

Upon opening the output file with "Read Intermediate Geometries" ticked an animation shows the reduction of the B-H bond length in each of the five steps. It is also notable that Gaussview does not show formal bonds for the first three steps of the optimisation (see below), it can be state then that for B-H bonds, the threshold for Gaussian to draw bonds is between 1.19 and 1.28Å.

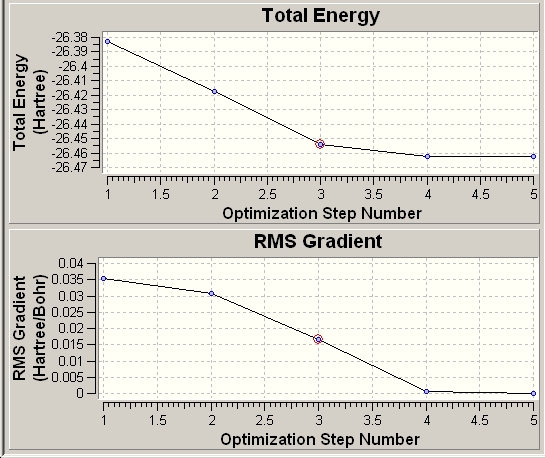
The graph of this data shows total energy of the molecule decreasing with each step of the optimisation. It also shows the derivative of this which also decreases with each step. This shows how the calculation method "hones in" on the lowest energy: the amount that energy is reduced between steps gets smaller each step as the energy approaches the minimum.

Vibrational Analysis

Vibrational Analysis of BH₃

	No.	Form of vibration	Frequency (cm-1	Intensity	Symmetry
	1	All H atoms bend into and out of plane of screen	1146	93	A2
	2	Symmetrical bend of bottom two hydrogens	1205	12	E'
	3	Top hydrogen bends in unison with bottom H-B-H unit	1205	12	E'
	4	All hydrogens stretch in unison	2593	0	A'1
	5	Asymmetric stretch of bottom two hydrogens	2731	104	E'
	6	Top hydrogen stretches as bottom two hydrogens contract, and vice versa.	2731	104	E'

Calculated infrared spectrum of BH₃

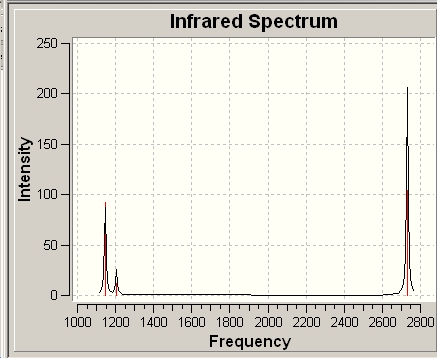
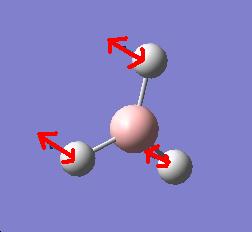
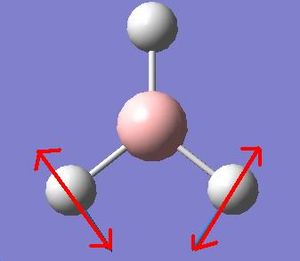
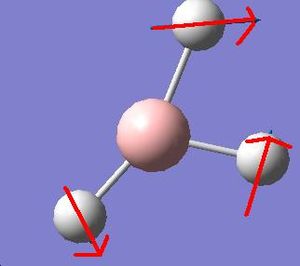
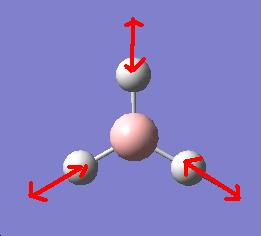
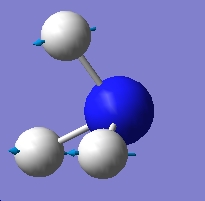
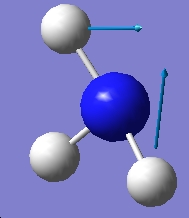
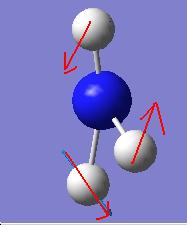
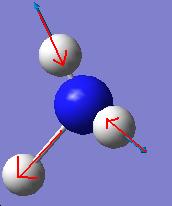
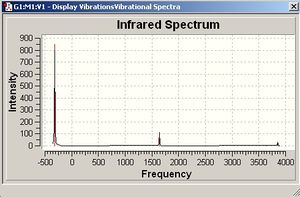
It is apparent that, despite there being six vibrational modes, there are only three peaks on the spectrum. There are two pairs of degenerate vibrations, so the two resultant peaks are superimposed upon one another, hence only one is visible. Also, vibration 4 does not result in a change in dipole hence is not IR active and gives a peak of zero intensity.

Molecular Orbitals

Vibrational Analysis of BH₃

	No.	Quantitative Orbital Surface	Qualitative
	1
	2
	3
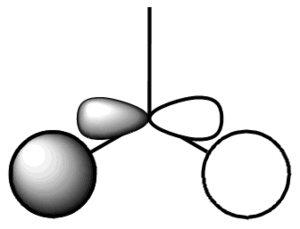	4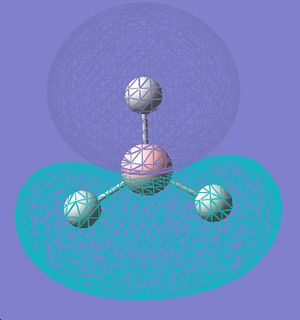
	5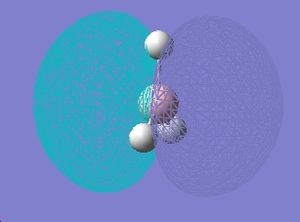

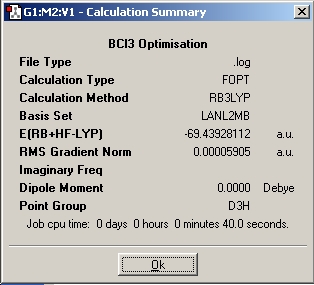
Qualitative MO diagram of BH3

BCl₃

BCl₃ wasdrawn in Gaussview and the symmetry restricted to D3h, tolerance was increased to "Very Tight". An optimisation was then run, again using the B3YLP method, but this time with a LanL2MB basis set as this incorporates a pseudopotential for the chlorine atoms (as Cl is a second row element). This was submitted to Gaussian.

The optimised B-Cl bond distance is 1.87Å Cl-B-Cl bond angle is 120.0^o

Small Molecule: HCN

As the molecule does not contain any atoms from the second row of the periodic table, it was deemed appropriate to use the 3-21G basis set to obtain a rough estimate.

Cis-Trans Isomerism

 This experiment will allow us to gain experience with basis sets and pseudopotentials by first creating a rough optimisation of the two isomers using a simple basis set requiring relatively little computing power, then optimising this further using a more accurate basis set with a pseudopotential for second row atoms.  This will reduce the overall computational time for optimisation as there is less conformational space needed to be explored by the more accurate and time consuming LANL2DZ basis set.

Firstly, the [Mo(PMe₃)(CO)₄] was drawn in Gaussview in the cis- and then the trans- form. These molecules were optimised using the LANL2MB basis set (B3LYP method). This was done with the keywords "opt=loose" added to ensure convergance occured. These roughly optimised structures were then reoptimised with the LANL2DZ basis set. This took notably longer than the initial optimisation. These fully optmiised structures were then subjected to frequency analysis: this resulted in the presence of no negative frequencies, this shows that an energy minimum was indeed obtained.

Vibrational Analysis of [Mo(PMe₃)(CO)₄]

	cis- Frequency	cis-Intensity	trans- symmetry (D4h)	trans-Frequency	trans-Intensity	trans- symmetry (D4h)
1	1849.7	1093.4	B2	1838.9	2004.3	eu
2	1850.8	1948.9	B1	1839.2	2003.6	eu
3	1870.3	337.0	A1	1882.6	0.0	b1g
4	1960.64	337.0	A1	1954.4	0.0	a1g

As can be seen from the Jmols, the cis structure has pseudo-C2v symmetry, whereas the trans structure has pseudo D4h symmetry.

Geometrical Parameters [Mo(PMe₃)(CO)₄]

	cis-	trans-
Mo-C bond length (angstroms)	1.98 (for 2CO on σv plane containing P atoms)2.03 (other 2COs ) (lit. 1.94, 2.03)	2.03 (lit. 2.05, 2.02)
Mo-P bond length (angstroms)	2.65 (lit. 2.52)	2.57 (lit. 2.50)

N.B. All lit values use Ph instead of Me, but bond lengths for the two compounds should be similar. It can be seen that a reasonable approximation of empirical bond lengths has been obtained from very simple computational methods.

Ammonia

B3LYP/6-31G

The next exercise was to investigate the inversion of the ammonia molecule.

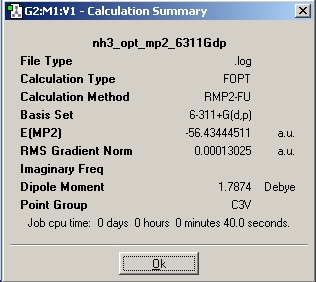
Firstly, NH₃ was drawn in Gaussview and optimised using B3LYP and the 6-31G basis set. This yielded C_3v symmetry and the calculation summary shown below.

Then another NH₃ molecule was created and one N-H bond length increased to 1.01Angstroms, thus altering its symmetry from C_3v to C₁. This was optimised as before, but with the "ignore symmetry" option checked. This meant that Gaussian did not try and alter the symmetry of the molecule, so it maintined its one long bond and its C₁ symmetry.

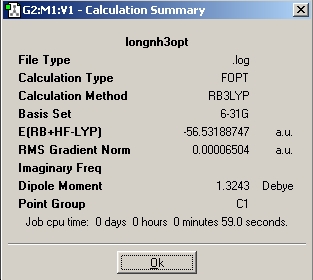
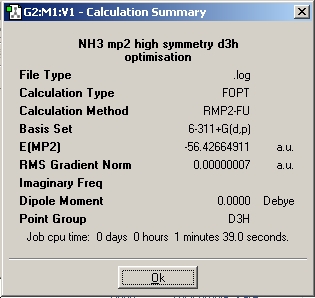
Next, a molecule of NH₃ with restricted D_3h symmetry was optimised. This is to represent the planar transition state of the inversion of ammonia.

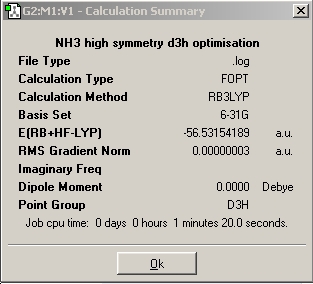
As can be seen in the cases of the C₁ and C_3v molecules, it would be expected that calculation time would be less for higher symmetry molecules. This is because fewer conformations are available to more symmetrical molecules, hence fewer iterations are usually needed to find the minimum energy. Although the D3h calculation in reality ended up taking the longest, this was likely due to other reasons, such as other programs running on the computer concurrently. By opening the output with intermediate geometries shown, it can be seen that it took just 3 iterative steps to obtain the minimum in the D3h molecule, c.f. 6 for the C3v and 8 for the C1 molecules.

	Symmetry
	D3h
	C1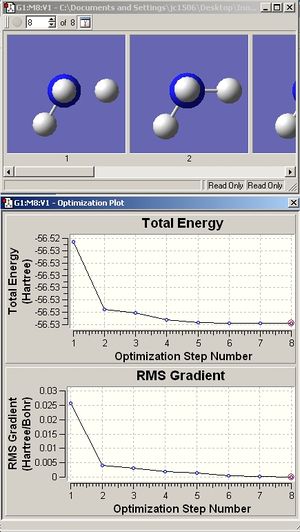
	C3v

As can be seen, the lowest energy molecule is, perhaps surprisingly, the one with C1 symmetry. The difference between the C3v and D3h configurations was calculated as -0.00034 Hartree, or -0.9 kJ/mol. This is a very low energy barrier, much greater than RT at ambient temps.

MP2

The C3v and D3h molecules were then recalculated using the MP2 method and the 6-311+(d,p) basis set. This is a higher level of calculation, hence the jobs took longer to run than there DFT-B3LYP counterparts.

As expected, the C3v symmetry is lower in energy, this method calculates the difference to be 0.0078 Hartree, or 20.5 kJ/mol. This is much much closer to the empirical value of 24.3 kJ/mol, this illustrates the benefit of using accurate methods and basis sets for small molecules such as ammonia.

Scan

Gaussian can be used to illustrate the inversion process of ammonia. By plotting the variation in energy with incremental changes in the H-N-c₃ axis, we can follow the movement of the hydrogens.

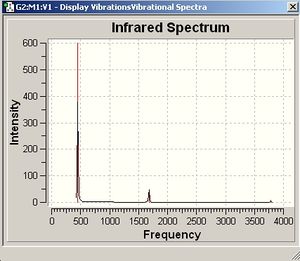
Vibrational Analysis

Vibrational Analysis of NH₃, showing in order, wavenumber, intensity and symmetry

Number	Form of Vibration (as shown for C3v	D3h	C3v
1		-318 (849.1) a2	452 (599.4) a1
2		1641 (56.0) e	1680 (41.7) e
3		1641 (56.0) e	1680 (41.7) e
4		3636 (0) a'1	3575 (0) a1
5		3854 (19.6) e	3576 (7.1) e
6		3854 (19.6) e	3576 (7.1) e

Lit. IR for C3v ammonia: 968, 1626, 3337, 3444

As can be seen, there are 6 vibrations for both molecules, however due to degeneracy only three peaks appear on the IR spectrum of C3v ammonia. It can be seen that the vibrations of the two geometries also match up and occur in the same frequency order. However, the D3h transition state has an infrared absorption of negative frequency. This corresponds to the "umbrella motion" where the molecule vibrates between two C3v structures. This vibrational mode is also the one which is least well matched to literature values in the IR spectrum of C3v ammonia, possibly as the approximations used inthe calculations do not take into account the quantum tunneling that causes the inversion of ammonia.

IR spectrum of c3v ammonia

Ir spectrum of d3h ammonia

Mini-project: Benzene and Borazine

Borazine, a 6 membered ring compound of alterating boron and nitrogen atoms, each bonded to one hydrogen, was first synthesised in 1926. It is isoelectronic to benzene and because of this great debate has ensued over its possible aromatic nature.

Benzene and borazine were drawn in Gaussian and optimised to the 6-31(d,p) level (b3LYP method). This method and basis set were chosen as all elements are first row and the basis set offers a happy medium between accuracy and calculation time. The symmetry of borazine had to be constrained to D3h. It is of interest that, whereas all C-C-C bond angles in benzene are 120 degreesm in borazine the B-N-B angle is 123.0 degrees and the N-B-N angle is 117.0 degrees

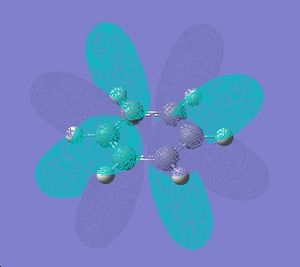
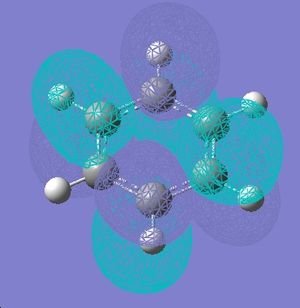
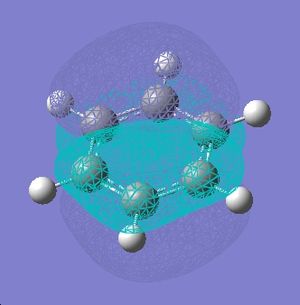
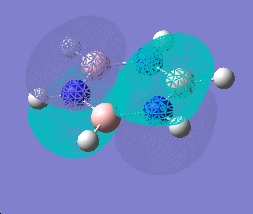
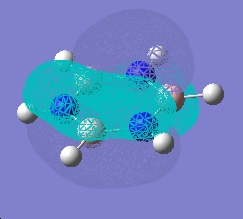
Below are the 6 orbitals of the pi system of benzene, and the equivalent orbitals in borazine

Table showing pi systems of benzene and borazine with relative energies.

	Benzene	Borazine
	0.124	0.877
	-0.017 -0.017	0.021 0.021
	-0.260 -0.260	-0.273 -0.273
	-0.373	-0.356

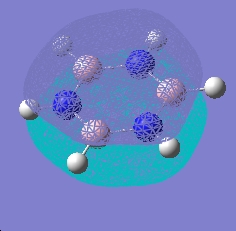As can be seen, the pi system of borazine is analagous to that of benzene, but orbitals shapes are skewed due to the difference in electronegativity between boron and nitrogen χ(N)-χ(B) = 1 (pauling scale), compared to benzene which obviously has no electronegativity difference due to the ring being made entirely of carbon. All bonding pi orbitals are filled, and all antibonding empty, much like benzene.

However, it is this electronegativity difference which dominates the reactivity of borazine. Unlike benzene, borazine is prone to addition reactions.

Forms of all occupied MOs for benzene and borazine

	Borazine	Benzene
21
20
19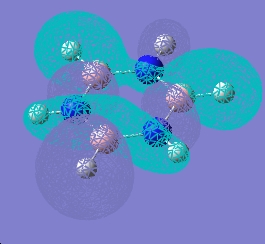
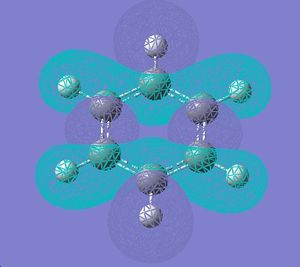18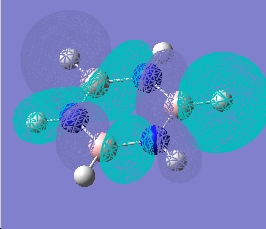
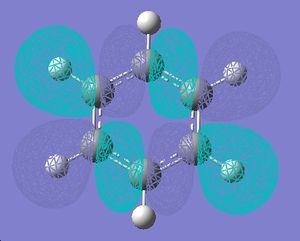17
16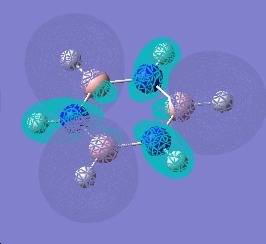
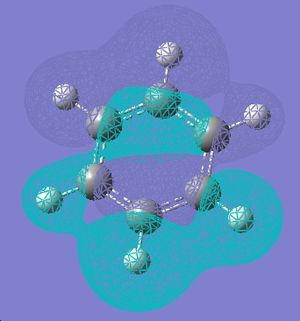15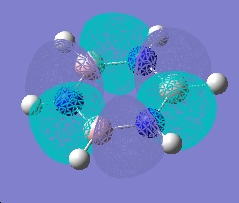
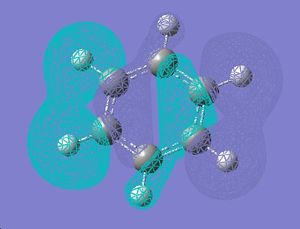14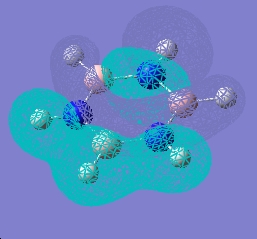
13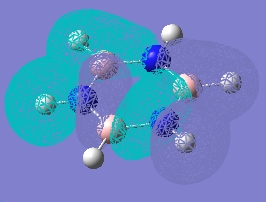
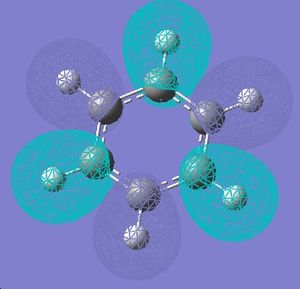12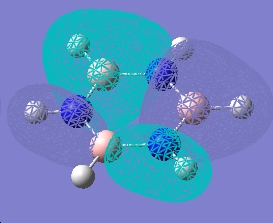
11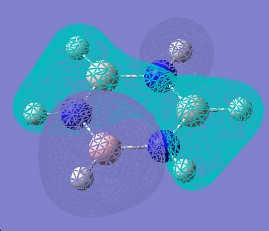
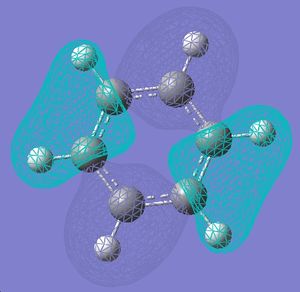10
9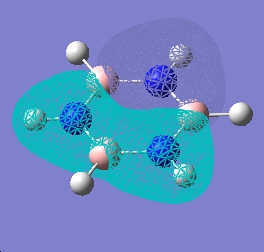
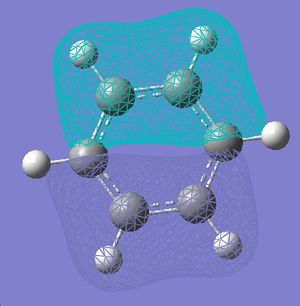8
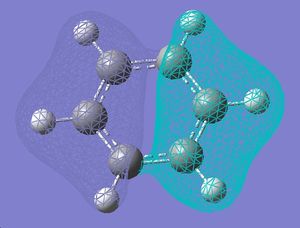7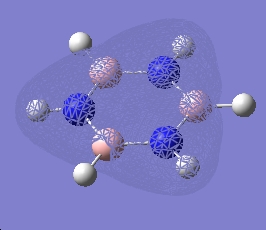
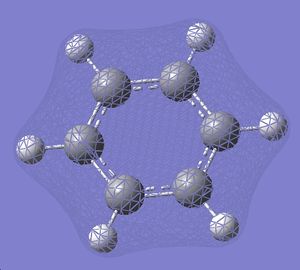6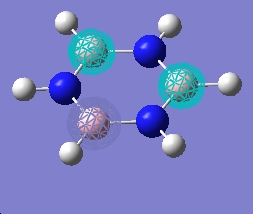
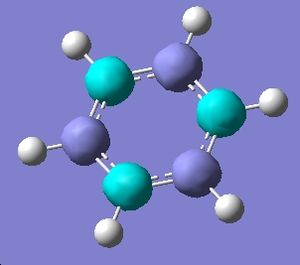5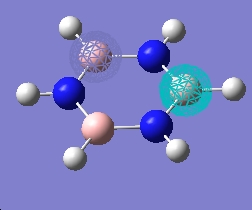
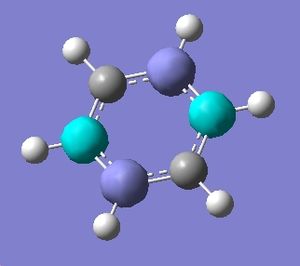4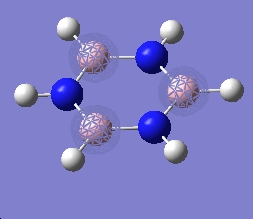
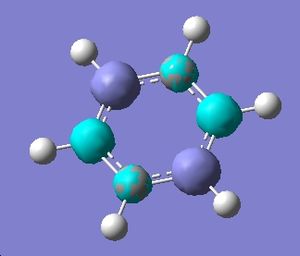3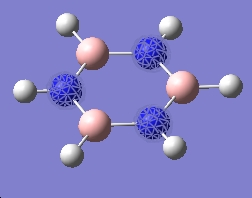
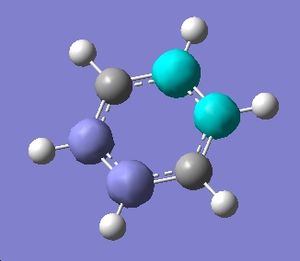2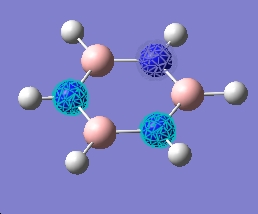
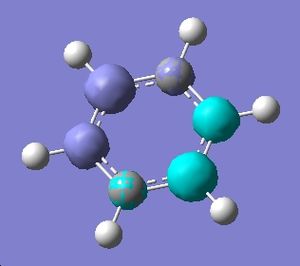1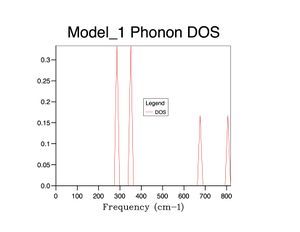

Vibrational Analysis

The vibration of greatest intensity in borazine is a bending of the hydrogens bonded to boron and nitrogen in opposite directions. However, this does not create a change in dipole moment in benzene and thus has nil intensity.

Benzene Spectrum

Vibrational Analysis of [Mo(PMe₃)(CO)₄]

Frequency (cm-1)	form	Intensity
3182		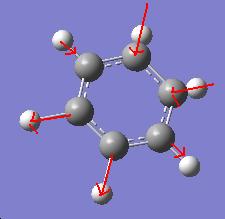125.2
3183		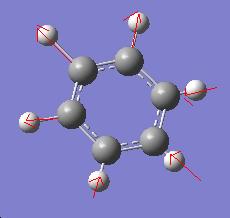37.6
687		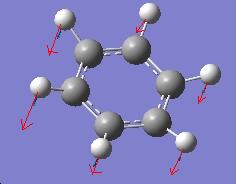37.6

Borazine Spectrum

Boron-Phosphorus Analogue

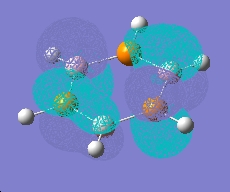
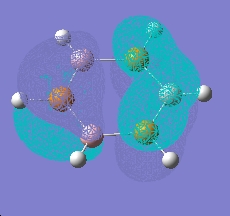
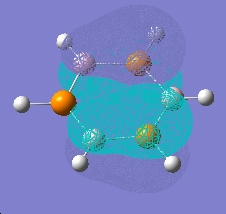
An analogue of borazine with nitrogen replaced by phosphorus was also created, this time optimised using a LAN2MB basis set, which offers a pseudopotential for the core electrons from second row phosphorus. A frequency and MO calculation was then run on this species.

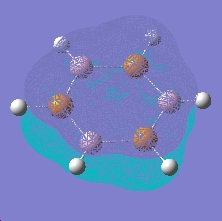As can be seen, this species shows the benzene type pi system orbitals. In reality, this molecule does not exist due to poorer overlap from the 3p orbitals of phosphorus (c.f. 2p of nitrogen)