JN1316Lab2

All distances are in Angstroms and energies in kCal/mol

Exercise 1: H + H ₂

What value do the different components of the gradient of the potential energy surface have at a minimum and at a transition structure? Briefly explain how minima and transition structures can be distinguished using the curvature of the potential energy surface.

The potential energy along a minima line has dV/dr = 0 and because it is a maxima d^2V/dr^2 is <0. A transition state also has dV/dr = 0 however d^2V/dr^2 is in contrast >0.

(This is mostly wrong. You need to refer to partial derivatives here. The TS is a saddle point where the first order partial derivative along any direction is 0, the second order partial derivative along the reaction coordinate is <0 and along the orthogonal coordinate is >0. Fjs113 (talk) 18:52, 14 May 2018 (BST))

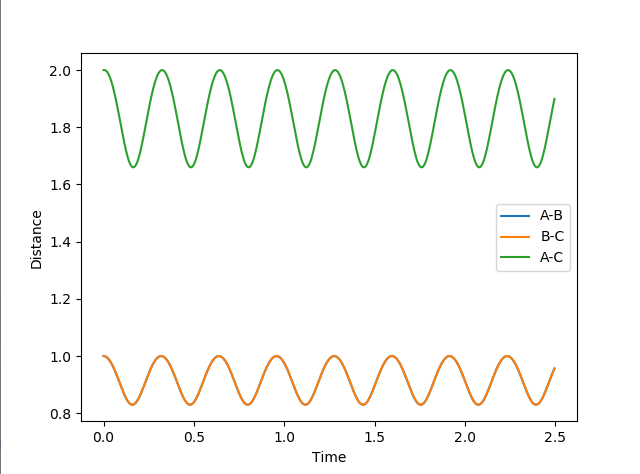
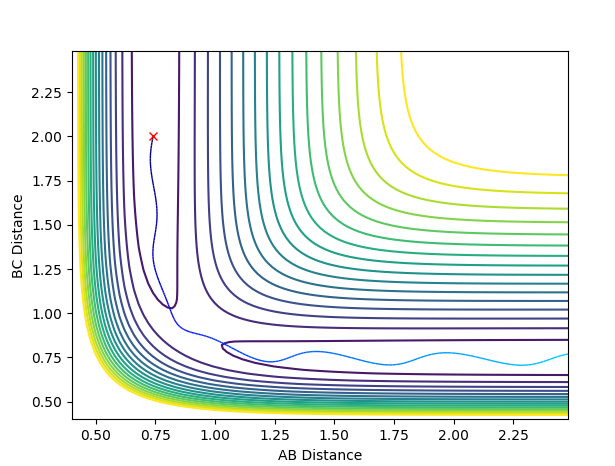
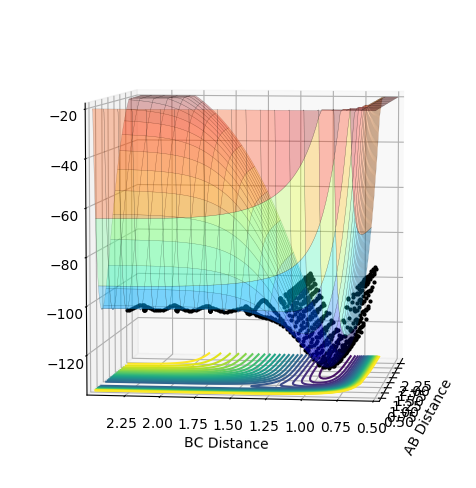
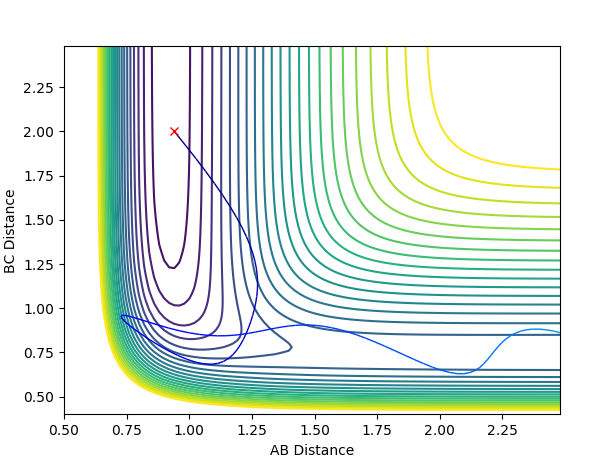
Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” plot for a relevant trajectory.

running an MEP calculation with both bond lengths set arbitrarily to 1 and exporting the data finds the saddle point to be where both bond lengths are 0.907741. The literature ^[1] is in agreement with this value.

(How did you get from the aforementioned MEP calculation to the saddle point? Whilst the bare number is correct, there is not enough explanation and evidence in the form of plots provided here. Fjs113 (talk) 18:52, 14 May 2018 (BST))

(Does this plot have to do something with your answer? If so, this is most certainly not the distances vs time plot obtained from your bond length value at the saddle point. You need to explain your figures! Fjs113 (talk) 18:52, 14 May 2018 (BST))

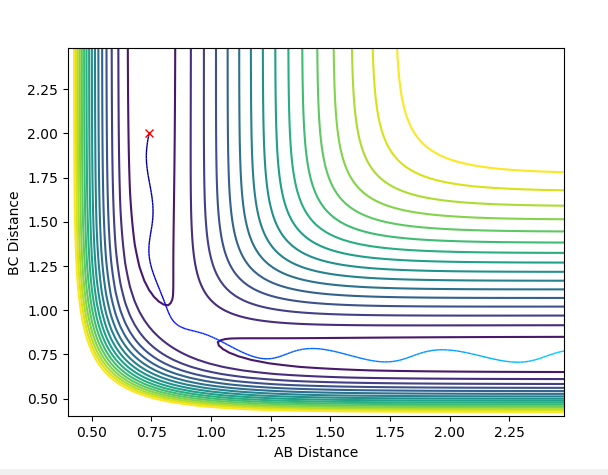
Comment on how the mep and the trajectory you just calculated differ.

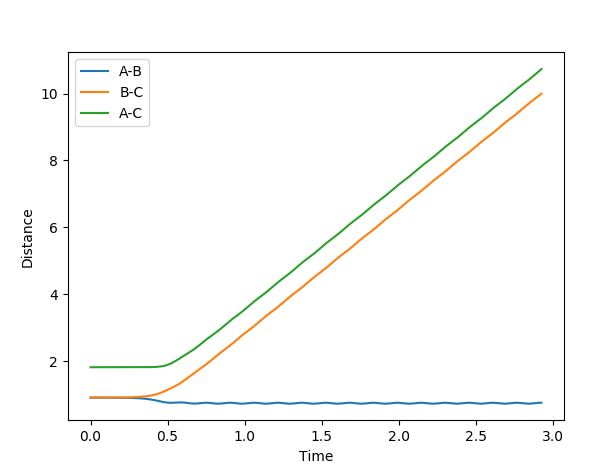
MEP plots correspond to infinitely slow motion with the velocity resetting to 0 in each step. This is not the case in dynamic plots. This explains why in MEP the molecular bond length does not vibrate and the free hydrogen atom does not escape to infinity but rather it's distance from the other two atoms plateaus.

(Again, you need to label your figures! Also, neither plot shows any plateauing as time progresses. In fact, in an MEP, it is very much possible for the lone hydrogen to escape to "infinity" with enough time. Fjs113 (talk) 18:52, 14 May 2018 (BST))

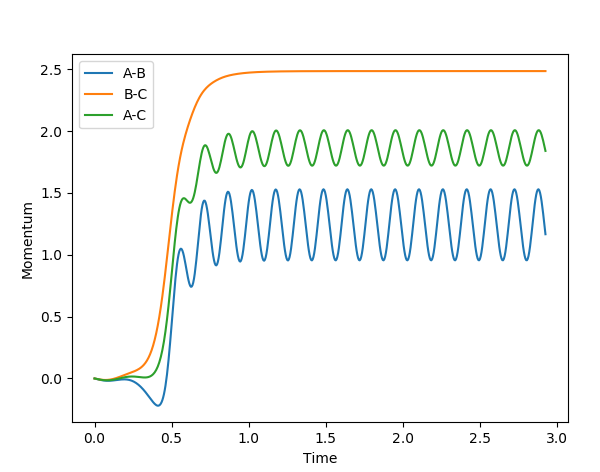
The momentum - time graph below shows that one hydrogen leaves as a free atom and the other 2 as a vibrating molecule with translational and vibrational energy modes.

(OK, but how does this tie in with your comparison of MEP vs Dynamics? Fjs113 (talk) 18:52, 14 May 2018 (BST))

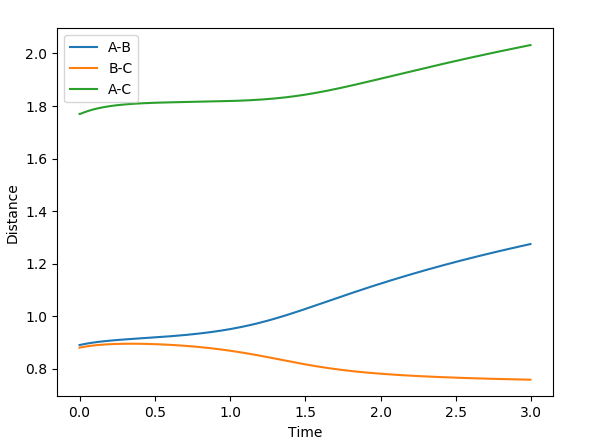
If it were switched so that r1 = rts and r2 = rts + 0.01 the central hydrogen would bond with the the hydrogen to its right as opposed to its left and the free hydrogen will be switched. This is because asides from the slight displacement in distance the system is symmetrical.

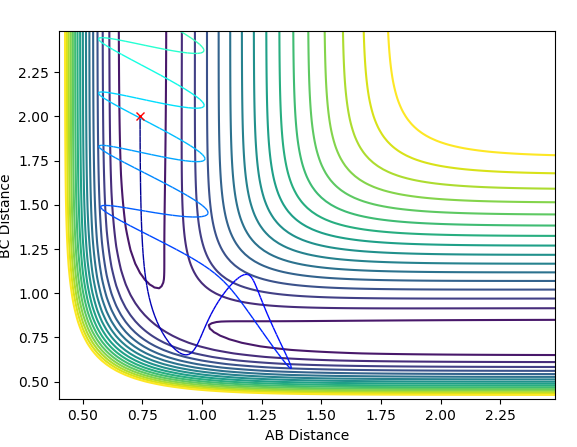
For the initial positions r1 = 0.74 Angstroms and r2 = 2.0 Angstroms, run trajectories with the following momenta combination:

p1	p2	Total Energy kCal/mol	Reactive?	Picture	Description
-1.25	-2.5	-99.018	Yes		A successful reaction with a vibrating reactant transferring vibrational energy to a vibrating product.
-1.5	-2.0	-100.456	No		There is not sufficient total energy for the reactants to overcome the activation energy.
-1.5	-2.5	-98.956	Yes		This simple reactive trajectory passes once simply over the transition state.
-2.5	-5.0	-84.956	No		This system has sufficient energy to overcome the activation energy. it does so but then 'bounces' of a steep wall of the potential well back to the reactants.
-2.5	-5.2	-83.416	Yes		The transition state theory assumes the potential barrier cannot be recrossed. This example violates that assumption as the potential barrier is crossed 3 times

(The picture for case 1 is not correct. Are you sure you put in the correct initial conditions. Fjs113 (talk) 18:52, 14 May 2018 (BST))

State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values? The main assumption to the TST is that once you have left the maxima that is the transition state you cannot go back to it or past it. This assumption fails as we have seen in the above trajectories some of the minimum energy paths reach the transition state and then return backwards. The TST also neglects the effects of quantum mechanics. Particularly for light particles such as hydrogen the non-zero probability of tunneling through a classically forbidden potential barrier with quantum potential is significant. Transition state theory will accurately predict reactions that pass only once over the transition state however it could incorrectly predict a path will be reactive or vice versa.

(Very good discussion, but how does this specifically affect predicted reactions rates? Fjs113 (talk) 18:52, 14 May 2018 (BST))

EXERCISE 2: F - H - H system

Classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?

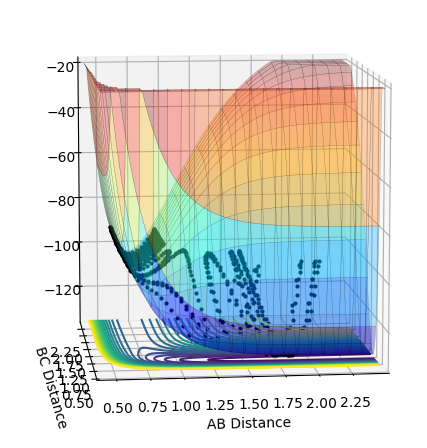
F + H2: Reaction is exothermic as H-F bond is stronger than H-H bond. As seen in the picture below the energy of the products is less than that of reactants.

H + HF: Reaction is endothermic as H-H bond is weaker than H-F bond. As seen in the picture below the energy of the products is greater than that of reactants. This can be found by inputting the output values from the previous computation

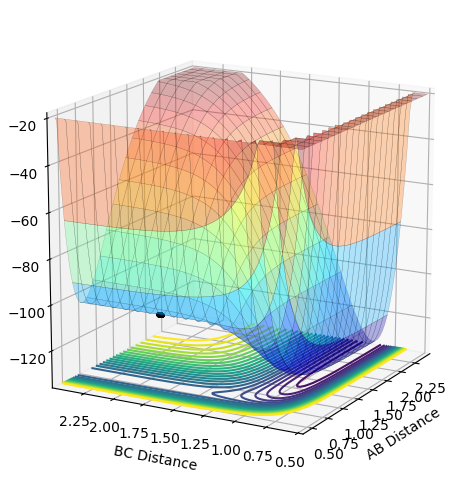
Locate the approximate position of the transition state.

Hammond's postulate states that the energy of the TS can be approximated as being that of the state nearest to it, because H2 + F is exothermic that means it is nearer the reactants therefore by inputting the distance values of the reactants and making the momenta = 0 the transition state can be found. AB = 0.74 and BC = 1.815. The energy of this state is -103.743. Therefore the activation energy of:

- H2 + F energy is -103.904 therefore activation energy is: 0.161

- HF + H energy is -137.063 therefore activation energy is: 33.32

In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. How could this be confirmed experimentally?

The momenta of the system increases after the reaction compared to before it. This can be seen in the animation of the interaction. Therefore the energy released in this reaction is converted to kinetic energy as the relationship between momentum and energy is Ek = p^2 / 2m. By measuring the temperature before and after and using the relationship Ek = 3/2*kT this can be confirmed empirically. While this investigates the translational modes, Raman spectroscopy investigates the vibrational energy modes. Other infrared methods including chemiluminescene can confirm this finding.

(Please be more specific here. In this reaction, potential energy is being converted to vibrational energy. You also need to be more specific about the experiments. What results would you expect to see. How would you related that back to the results from the simulation? Fjs113 (talk) 18:52, 14 May 2018 (BST))

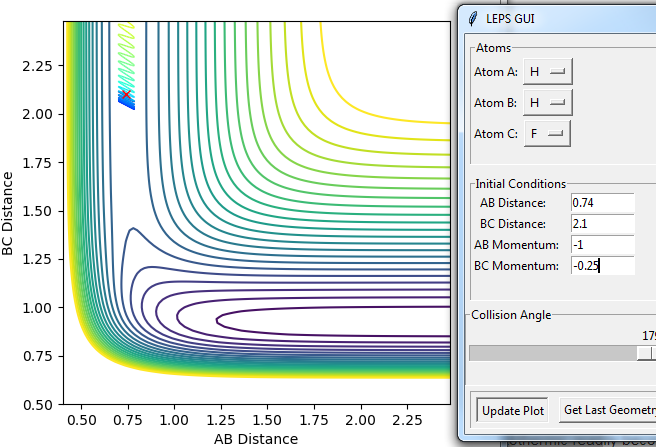
Setup a calculation starting on the side of the reactants of F + H2, at the bottom of the well rHH = 0.74, with a momentum pFH = -0.5, and explore several values of pHH in the range -3 to 3 (explore values also close to these limits). What do you observe?

Despite the fact that there is sufficient energy in H-H to overcome the activation energy the H-H molecule collides and bounces off of the fluorine atom when P(H-H) is -3. This can be rationalized as an H atom having enough energy to reach the bottom of the H-F potential well and then exit it again, the same is true for the momentum being +3.

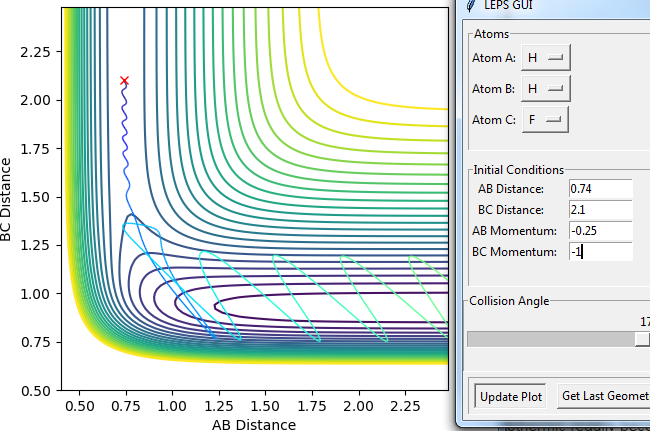
For the same initial position, increase slightly the momentum pFH = -0.8, and considerably reduce the overall energy of the system by reducing the momentum pHH = 0.1. What do you observe now? Under these conditions the reaction proceeds successfully

(Please provide some pictures for evidence. Fjs113 (talk) 18:52, 14 May 2018 (BST))

for H + HF Setup initial conditions starting at the bottom of the entry channel, with very low vibrational motion on on the H - F bond, and an arbitrarily high value of pHH above the activation energy (an H atom colliding with a high kinetic energy).

Under these conditions the incoming high energy Hydrogen collides with the HF molecule and bounces off in the direction it came from taking the other Hydrogen with it, in this way the reaction proceeds.

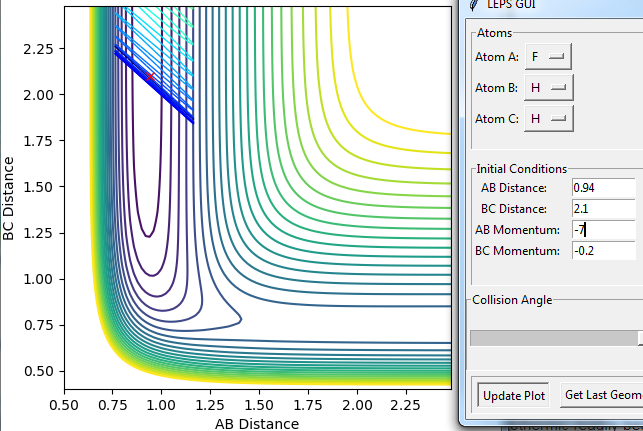
Try to obtain a reactive trajectory by decreasing the momentum of the incoming H atom and increasing the energy of the H - F vibration. (It may be difficult to find the initial conditions that generate a reactive trajectory for this reaction. Using the inversion of momentum procedure for a trajectory starting on the transition state can be useful in this case. Working on the Skew Plot framework could also be helpful.)

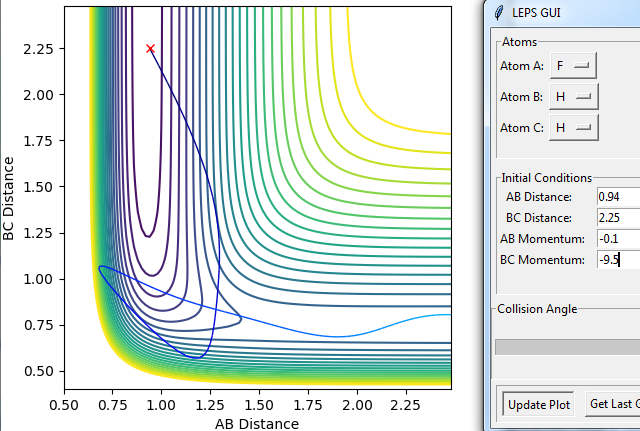
Using the inversion of momentum procedure it can be found that the the highest p(HF) and lowest p(HH) that gives a reactive trajectory is 2 and -6.8 respectively. The result of this is pictured below.

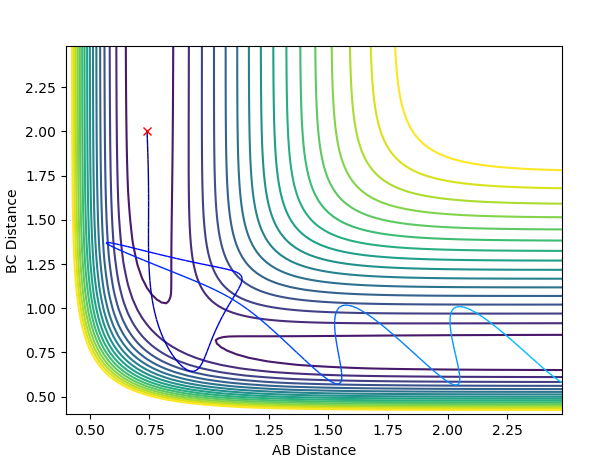
The cases studied are an illustration of Polanyi's empirical rules. Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.

Polanyi's emperical rules state that for an early barrier reactions the translational energy mode is more efficient than vibrational energy in achieving a reactive trajectory, while the opposite is true for late barrier reactions ^[2] . Exothermic reactions have early transition states while endothermic reactions have late transition state. With that in mind the reaction of F with H-H which is exothermic readily becomes reactive with a small increase in translational energy whereas an increase in vibrational energy does little to progress the reaction. In contrast H with H-F responds to a small increase vibrational energy very strongly and will overcome the activation energy, whereas an increase in translational will have a less efficient effect on the system achieving a reactive trajectory. The 4 examples below demonstrate this with H + H-F and F + H-H systems:

(This is good! Fjs113 (talk) 18:52, 14 May 2018 (BST))

References: 1: he Journal of Chemical Physics 22, 1142 (1954)

2: G. Czakó, J. M. Bowman, Science 2011, 334(6054), 343–346