Insfd
Module Two: Inorganic Molecular Modelling
BCl3
A BCl3 molecule was created in GaussView and its geometry optimized using the B3LYP method and 3-21G basis set. The optimized B-Cl bond length 1.77503 Å and the optimized Cl-B-Cl bond angle is 120°. The following is a summary of the calculation and geometry.
| File Type | .log |
|---|---|
| Calculation type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | 3-21G |
| Final energy in atomic units | -1398.80444943 |
| Dipole Moment in debye | 0.00 |
| Point Group | D3h |
| Time Taken | 18 seconds |
A Small Molecule
SO2ClF was the molecule chosen for this part of project. The optimized S=O bond length is 1.56248 Å and the optimized O-S-F angle is 107.762°. The S-O bond length is a little longer than that shown in SO2. This is probably due to the electron withdrawing nature of fluorine and chlorine.
A summary of the calculation is shown below.
| File Type | .log |
|---|---|
| Calculation type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | 3-21G |
| Final energy in atomic units | -1102.92453346 |
| Dipole Moment in debye | 0.6422 |
| Point Group | C1 |
| Time Taken | 3 minutes and 2 seconds |
The coordinates of the atoms in the optimized molecule are shown below.
Coordinates: --------------------------------------------------------------------- Center Atomic Atomic Coordinates (Angstroms) Number Number Type X Y Z --------------------------------------------------------------------- 1 16 0 -0.520821 0.000000 -0.129846 2 8 0 -1.042907 1.372779 -0.663005 3 8 0 -1.042907 -1.372779 -0.663006 4 17 0 1.839688 0.000000 -0.077250 5 9 0 -0.695006 -0.000001 1.555431 ---------------------------------------------------------------------
BH3
The BH3 molecule was modelled and its geometry optimized using the B3LYP method and 3-21G basis set. A summary of the optimization is shown below.
| File Type | .log |
|---|---|
| Calculation type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 3-21G |
| Final energy in atomic units | -26.46226433 |
| Dipole Moment in debye | 0.00 |
| Point Group | C3v |
| Time Taken | 12 seconds |
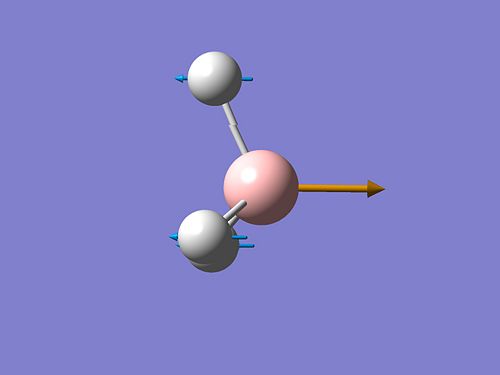
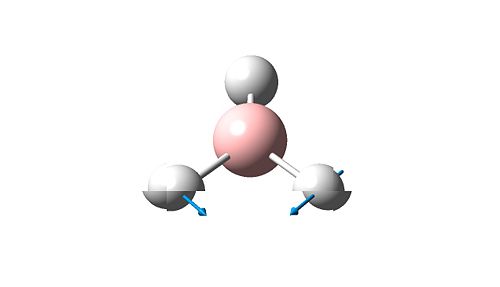
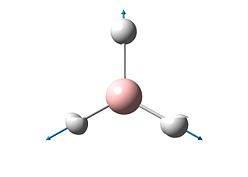
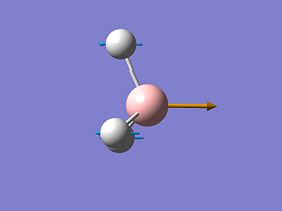
A frequency analysis of this molecule was submitted to Gaussian. (The resulting energy was the same as the energy obtained in the optimization step). The vibrational modes are shown below.
The molecular orbitals of BH3 were calculated. These can be seen below.
| The HOMO-3 | The HOMO-2 | The HOMO-1 |
|---|---|---|
|

|

|
| The HOMO | The LUMO | The LUMO+1 |

|

|

|
| The LUMO+2 | The LUMO+3 | |
|
|
A localised version of the molecular orbital diagram of BH3 has been shown below. It should be possible to match the computed orbitals with those derived manually. This is done in the table below the molecular orbital diagram.
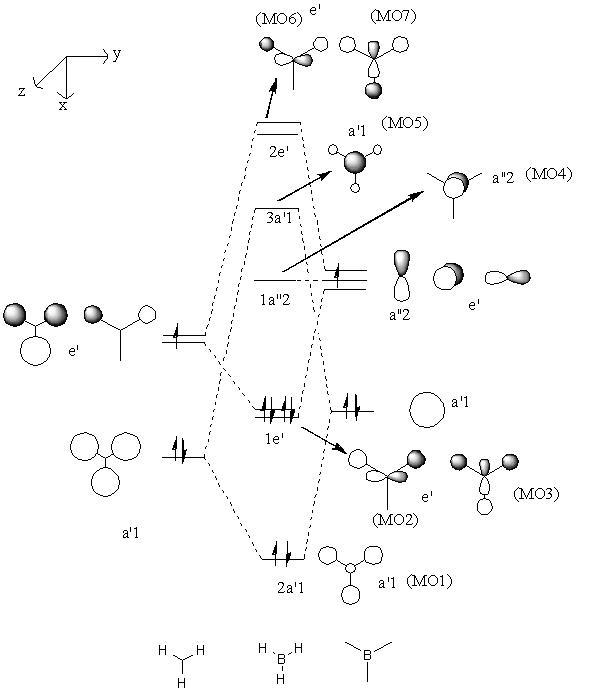
| MO1 | MO2 | MO3 |
|---|---|---|

|

|

|
| MO4 | MO5 | MO6 |

|

|

|
| MO7 | ||

|
Cis and trans isomerism in a transition metal complex
Cis and trans isomerism in the complex Mo(CO)4PCH3. The geometry of the both the cis and the trans complex was optimized in two steps (using the B3LYP method and firstly the LANL2MB and then the LANL2DZ basis sets). The final optimized complex(the geometry resulting from the LANL-2DZ basis set) has been published in chemical database D-space. (For the cis- isomer the URL is http://hdl.handle.net/10042/to-1198); for the trans isomer the URL is http://hdl.handle.net/10042/to-1198)
|
| ||||||
| The optimized cis complex | The optimized trans complex |
Geometry
The geometry of the trans-complex is like octahedral geometry. The C-Mo-P angle is 91.069 degrees and the C-Mo-C angle is 89.952. The CO groups occur the equatorial positions and the PMe3 groups occupy the axial positions. The C=O bond length is 1.18981 angstroms and the Mo-C bond length is 2.02858 angstroms. The distance between Mo and P is 2.57191 angstroms. This is not shown as a bond by Gaussview, as it is considered too long.
The geometry of the cis complex is also almost octahedral (the P-Mo-C angle is 89.596° and the C-Mo-C angle is 90.420). The C=O bond length is 1.19125 angstroms, the Mo-C bond length is 1.98255 angstroms and the Mo-P bond length is 2.65182 angstroms.
Both complexes are compared to the literature[1]
| Geometric parameter | Cis-isomer | Trans-isomer | Literature value (for cis-Mo(CO)4(PMe2Ph)2 ' |
| C-O bond distance | 1.188 Å | 1.190 Å | 1.14 Å |
| P-Mo-P bond angle | 95.28° | 179.99° | 94.78° |
| (trans-) C-Mo bond length | 2.032 Å | 1.190 Å | 2.016 Å |
| (Cis-) C-Mo bond length | 1.983 Å | 1.190 Å | 1.982 Å |
| Mo-P bond length | 2.651 Å | 2.572 Å | 2.529 Å |
| P-C length | 1.893 Å | 1.890Å | 1.84 Å |
| Mo-P-C bond angle | 118.30° | 117.14° | 116° |
| C-P-C bond angle | 100.97° | 101.42° | 101.9° |
As can be seen from the above comparison, the bond lengths computed here agree well with those found in the literature. All the C-O bond lengths are the same in the trans complex; this is expected, as all CO positions are equivalent. The CO bond lengths are comparable to those in carbon monoxide.
Frequency Analysis
A frequency analysis was then done on both molecules. Both molecules showed negative vibrational modes, the cis complex at -5.1777 cm-1 and the trans complex at -12.386 and -8.9205 cm-1. This fact is discussed in the next section.
Negative vibrational modes
- Negative vibrational modes mean that the true energy minimum has not been found. Instead, the calclulation has found a transition state. This happens because of the method used by Gaussian to find the minimum. The coordinates of the atoms are varied and a first and second derivative is taken. If the first derivative (the force) is equal to zero then a minimum or maximum has been achieved. The second derivative can be used to distinguish between these two stationary points (a minimum has a positive second derivative whereas a maximum has a negative second derivative). Gaussian then checks that this value is a minimum by changing the r slightly and assessing the magnitude of the resultant energy change. If the change is large then it considers that it has found the minimum. If it is small then it continues. However, due to numerical rounding errors Gaussian does not usually find exactly zero. Instead it accepts from about -5 to +5 as zero. Therefore, if the potential energy surface is shallow it may not find the lowest energy geometry. Also, if the transition state is shallow it may consider this to be a minimum.
- In my calculation it found 4 negative vibrational modes, but since two of these were within the error range it accepted these as zero. The other two were considered too negative and were therefore not included.
Low frequencies --- -12.3871 -10.5818 -5.7422 -1.6915 0.0001 0.0003 Low frequencies --- 0.0005 5.4930 45.2816 ****** 2 imaginary frequencies (negative Signs) ******
- The fact that the geometry was not fully optimized doesn't really matter in this case, as the negative vibrations and the important C=O stretches do not couple. Thus the diagnostic C=O are not affected by the change in geometry from lowest energy conformer and transition state. Also, since the vibrations are centro-symmetric, there is (in theory) no change in dipole. This means that it should not be IR active. The fact that it has any IR intensity is because Gaussian has assigned C1. This is not correct, but since the molecule is not perfect Gaussian does not recognise any symmetry. This means that the vibrations are not quite symmetrical, involve a slight change in dipole and therefore have some IR intensity.
Since this problem does not really affect the IR spectrum, I will go on and analyse the strongly IR active vibrations. These have been compared to literature[2] values for Mo(CO)4(PPh3)2.
| Frequency (cm-1) | Assigned Vibration | IR intensity | Literature frequency (cm-1) |
|---|---|---|---|
| 1838.58 | Asymmetric CO stretch | 1999.46 | 1899 |
| 1838.8 | Asymmetric CO stretch | 2007.25 | 1911 |
| 1882.27 | Symmetric CO stretch | 0.0005 | 1929 |
| 1954.06 | Symmetric CO stretch | 0.0001 | 2023 |
Optimizing the energy of the complex
The trans complex is lower in energy than the cis complex. This is not suprising due to the fact that we expect steric repulsion between the two PMe3 groups.
Ammonia
Ammonia was investigated in order to compare the effect firstly of the symmetry of the molecule and then the various basis sets and methods and secondly in order to investigate the pathway of its inversion. An ammonia molecule was created and optimized using the 6-31G basis set and the B3LYP method. The symmetry assigned to this molecule by Gaussian is C3v.

A new ammonia molecule was generated, this one with one bond lengthened to 1.01 angstroms. This was done using the modify bond length tool. The geometry of the new molecule was optimized and the summary is shown below (the symmetry given was C1.
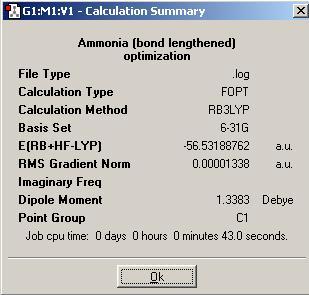
Finally, a modified ammonia molecule with D3h symmetry (could be used to model the transition state in the inversion of ammonia) was optimized. The summary of the optimization is shown below (the symmetry of the molecule is unsuprisingly assigned as D3h.
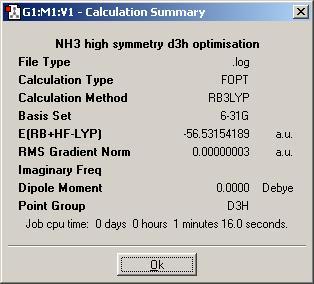
The molecule with the lengthened bond is the lowest in energy and the difference in energy between the highest energy geometry and the lowest energy is 3.4573x10-4 a.u. = 0.9077 kJ/mol. This energy is not significant, as it is much lower than RT (which is around 2.5 kJ/mol).
It is now possible to compare the effect of the symmetry of the input molecule on the calculation. It seems that the starting symmetry has made any difference to the final structure, as the molecules produced all have different energies and dipole moments. Further, the starting symmetry has affected the time the calculation took to run: the higher the symmetry the longer the calculation takes to run (this is slightly conterintuitive and is discussed below.) The starting symmetry would be less important if a molecule could break symmetry during a calculation, but this only occurs if there is an error in calculation. If there is, the molecule may be outputted with a different geometry than it was inputted with (as in the BCl3 example). Calcuations with high symmetry are predicted to take a lot of cpu time.
The method and basis set were then varied. The calculation was run with the DFT and B3LYP method with the 6-311G+(d,p), the MP2 version of the same and with "opt mp2=full/6-311+g(d,p)".
The optimization of C3v ammonia using the DFT and B3LYP method took 38 seconds; around the same amount of time as the last set of calculations. This is expected, as the same basis set was used.
The calculation run with the MP2 method and the 6-311G(d,p) basis set to 37 seconds to run (it had an energy of -56.43444511 hartree and the correct point group of C3v.) This is a much shorter time than expected, as higher level calculations should have tighter optimization parameters and thus will not converge as quickly. I am unsure why there is no increase, unless it is because the starting molecule used (from the default templates found in GaussView) was already very close to optimal and so there was no great difference in calculation because there wasn't much to change.
The D3h high symmetry calculation took 1 minute and 46 seconds to run (its optimized energy was -56.42664911 hartree and its point group was D3h). This again completed faster than expected as the lower level basis set calculation of the same molecule (D3h ammonia) took a comparable amount of time. I can only suggest the same reason as above for why this is the case.
The barrier height to the inversion of ammonia can be deduced by subtracting the energy of the ground state (C3v ammonia) from the energy of the transition state (D3h ammonia. From the calculations above, this is 7.796x10-3 hartree (20.468398 kJ/mol). The barrier of inversion as calculated by the last set of calculations is 0.903198255 kJ/mol; delta E in the first set is 3.4401x10-4. This is 22 times smaller than the energy calculated using the higher basis sets.
The higher basis set delta E comes much closer to the experimentally determined barrier of inversion of -24.3 kJ/mol. Since this is the case, and there is not much difference in the time taken to complete the higher level calculations, it is conlcuded that it is much more beneficial to use the higher basis set, the approximation to real life is much better. It is still not perfect, but it is comparably close.
Vibrations
The vibrations computed for C3v ammonia are shown below.
| # | Frequency (cm-1 | Corresponding vibration |
|---|---|---|
| 1 | 452.302 (IR = 599.472) | "umbrella motion" |
| 2 | 1680.47(IR = 41.7256) | "swimming wag" |
| 3 | 1680.47 (IR = 41.7245) | "one-armed push" |
| 4 | 3575.43 | Symmetrical stretch |
| 5 | 3775.76 (IR = 7.0892) | "knock-on effect" |
| 6 | 3775.76 (IR = 7.0884) | "the punch" |
The IR spectrum of C3v ammonia is shown below.

The theoretical vibrational modes shown above can be compared with those recorded in literature[3]. An IR spectrum of solid NH3 showed four key vibrational modes at 3210, 1075, 3375 and 1625 cm-1. The predicted vibrations compare reasonably well with literature, except that we seem to be missing the vibration at 1075 cm-1.
These can be compared to the vibrations compared to the ones computed for D3h ammonia.
| # | Frequency (cm-1 | Corresponding vibration |
|---|---|---|
| 1 | -840.58 (IR = 487.811) | "umbrella motion" |
| 2 | 1587.95 (IR = 43.6005) | "swimming" |
| 3 | 1587.95 (IR = 43.6005) | "one-armed push" |
| 4 | 3676.66 (IR = 0) | Symmetrical stretch |
| 5 | 3894.23 (IR = 60.0321) | "knock-on effect" |
| 6 | 3894.23 (IR = 60.0321) | "the wagging punch" |
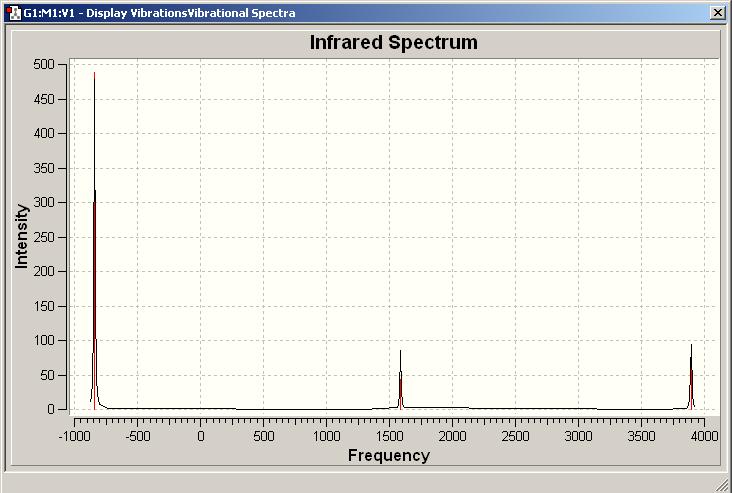
There are 6 positive vibrations for the C3v structure and the 5 positive vibration for the D3h structure. There is one negative vibrational mode in D3h ammonia, as this is a transition state. The particular negative vibration (-840.58 cm-1 corresponds to the inversion mechanism: since the vibration is negative this "umbrella" vibration results in a lower energy (what we expect, as it gives C3v ammonia. Since C3v ammonia is the ground state there should never be any negative vibrations (unless the geometry has not optimized properly). The vibrations of the two different symmetries of ammonia are very similar, it is possible to match them up.
| # vibration (C3v) ammonia | # vibration (D3h) ammonia |
|---|---|
1 
|
1 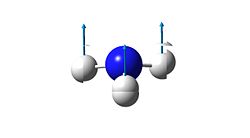
|
2 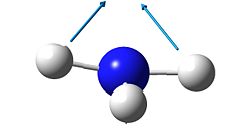
|
2 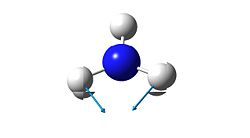
|
3 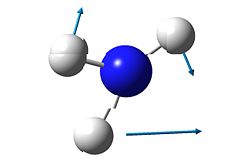
|
3 
|
4 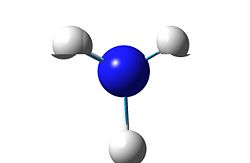
|
4 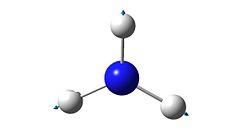
|
5 
|
5 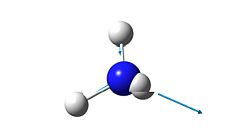
|
6 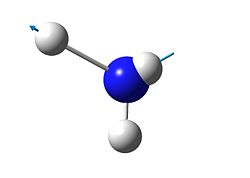
|
6 
|
As mentioned before, the "umbrella" type vibration corresponds to the inversion pathway. This vibration is the number one in both the ground state and the transition state (-840.58 cm-1 in the transition state and 452.302 cm-1 in the ground state.
Mini-project
The aim of this project is to investigate the reactivity of white phosphorus. This will be done using modelling and computing the molecular orbitals. Specific reactions will then be considered by modelling the products and then comparing the relative energies. All molecules will be optimized three times using the DFT and B3-LYP methods with the STO-3G, LANL2MB and the LANL2DZ basis sets except where otherwise stated.
White Phosphorus
A white phosphorus molecule was created in ChemBio3D and tranferred to GaussView. Its geometry was then optimized using the mthods and basis sets detailed above. The resulting geometry is shown below. Bonds have not been displayed by GaussView, as they are longer than what it takes to be a bonding length. This is probably because the bonds are not conventional 2 centre 2 electron bonds and are more akin to cluster bonding. This can be investigated by looking at the computed molecular orbitals.
White Phosphorus |
Below is a summary of the optimization.
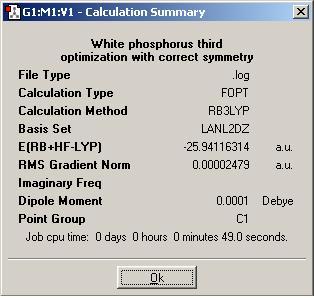
As can be seen from the summary, Gaussian has not identified the correct point group of phosphorus (this is tetrahedral). At first, this fact was unsuprising as the molecule had not been entered with perfect tetrahedral symmetry. The input file was then modified (as shown below) to fix all bond lengths and all bond abgles to be equal. This was checked by opening the file in GaussView first. However, the symmetry was still lost after the optimization had run. The direct result of the incorrect symmetry assignment is that the molecular orbitals computed by Gaussian will not be correct (the symmetry will be wrong). Since the molecular orbitals will still be a reasonable approximation I will continue to look at them and try to rationalize how they affect the reactivity of white phosphorus. I have only presented a few of the orbitals that I find interesting.
| LUMO | 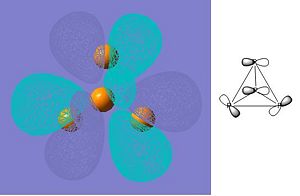
|
HOMO | 
|
| HOMO-1 | 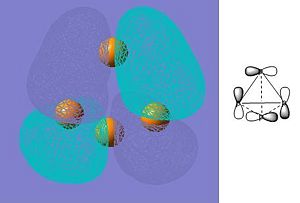
|
HOMO-5 | 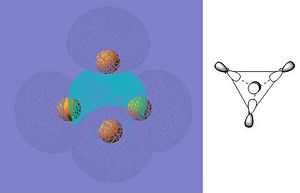
|
These orbitals confirm that the bonding in white phosphorus is not conventional but is delocalised over the whole molecule. The conventional explanation (based on Lewis structures) explains the reactivity of white phosphorus in terms of the availability of its lone pairs, however a molecular orbital approach does not rely on this. Reactivity in the MO approach can be rationalized using the relative energies of the frontier orbitals of the reactants: the higher energy HOMO will attack the lower energy LUMO. This means that the molecule with a comparatively high HOMO will be reactive. In order to comment on the reactivity of white phosphorus it will be necessary to compute the HOMO and LUMO energies of some other molecules that it reacts with, as it will then be possible to see which has the highest energy HOMO. (The energy of the LUMO is -0.100 hartree and the energy of the HOMO is -0.267 hartree.) Molecular orbital theory says nothing about strain, however, and white phosphorus is very strained due to the fact that the bonding angles are contrained to 120 degrees. This is a limitation of this approach, as the reactivity of phosphorus will not be fully explained.
A frequency analysis of white phosphorus was also computed. This was done mainly to check that the geometry had correctly optimized, as white phosphorus is not IR active. Since there were no negative vibrational modes it can be assumed that the geometry found does reflect the true minimum.
P2
White phosphorus is in equilibrium with P2 at room temperature. It is therefore interesting to compare the energies of these two molecules and deduce which will be more abundant. The geometry of P2 was optimized using the same basis sets. (This time the correct point group of D∞h was found. This means that the molecular orbitals computed will be correct.)
The energy of this molecule is -12.96529980 hartree. This is -34040.39462 kJ/mol. -68108.52382 The energy difference between P4 is -34068.1292 kJ/mol. This suggests that the equilibrium is biased towards white phosphorus rather than P2. This is what was expected, as P2 is not a very naturally abundant molecule whereas white phosphorus is considered to be the natural state of phosphorus.
| HOMO-4 | 
|
HOMO-3 | 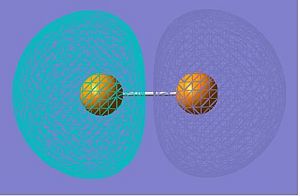
|
|---|---|---|---|
| HOMO-2 | 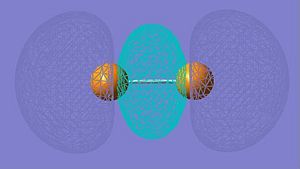
|
HOMO-1 | 
|
| HOMO | 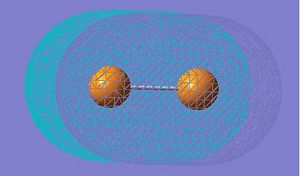
|
LUMO | 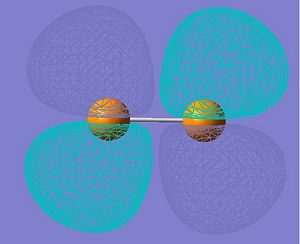
|
| LUMO+1 | 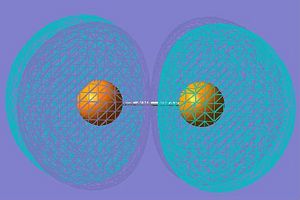
|
LUMO+2 | 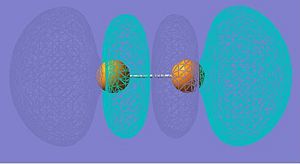
|
The computed molecular orbitals can be compared to those predicted by a qualitative MO diagram. The qualitative MO diagram for P2 has been drawn and can be seen below.
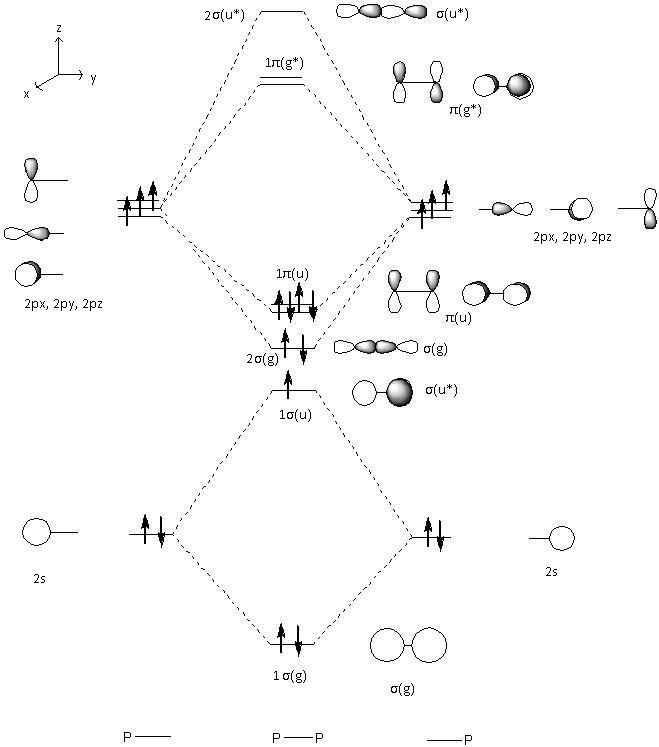
It is now possible to match up the qualitiative and the computed molecular orbitals. As can be seen from the table below, these compare well. It is possbile to see the sigma, pi, sigma antibonding and pi antibonding orbitals.
| Computed molecular orbital | Qualitative molecular orbital |
|---|---|
| HOMO-4 | 1σg |
| HOMO-3 | 1σu* |
| HOMO-2 | 2σg |
| HOMO-1 | 1πu |
| HOMO | 1πu |
| LUMO | 1πg* |
| LUMO+1 | 1πg* |
| LUMO+2 | 2σu* |
This molecule will not be compared to white phosphorus in terms of the reactivity of white phosphorus as it does not take part in a reaction with white phosphorus, it is formed from white phosphorus.
The reaction of white phosphorus with halogens
White phosphorus reacts very strongly with all the halogens to give either PX3 or PX5. Which one is formed depends on the amount of halogen available to react. In this project, I will focus on the reaction with flourine.
PF3 and PF5 were modelled and optimized. Their energies were -306.084 hartree (-803623.542 kJ/mol) and -505.737 hartree (-1327812.494 kJ/mol). PF3 was correctly assigned the C3v point group, but PF5 was incorrectly assigned C1 despite the fact that the molecule had been entered with equal bond lengths.
| PF3 |
|
PF5 |
|
The reactivity of white phosphorus towards these reactions can be rationalized by comparing the energies of the HOMOs of F2 and white phosphorus. The LUMO of F2 has an energy of -0.195 hartree. This is lower than the HOMO of white phosphorus and so F2 will be attacked by white phosphorus. This is a vigorous reaction, as this energy difference is actually quite large in terms of kJ/mol (249 kJ/mol).
The reaction of white phosphorus with LiPH2
White phosphorus reacts with LiPH2 to produce Li2P16 according to the reaction scheme below.
23P4 + 12LiPH2 → 6Li2P16 + 8PH3
The structure shown below is the Li2P162- ion. This ion is related to Hittorf's and fibrous red phosphorus, and so can also be seen as a model of red phosphorus.
Pentahelicene |
The energy of the optimized molecule is -104.08168404 hartree ( = -273266.46 kJ/mol.) This suggests that red phosphorus is thermodynamically more stable than white phosphorus, explaining why white phosphorus slowly converts to red phosphorus over time (the reason why white phosphorus is sometimes known as yellow phosphorus).
The reactivity can also be rationalized by comparing the energies of the HOMO and LUMO of white phosphorus and LiPH2. This time, LUMO of LiPH2 is higher than the HOMO of white phosphorus, but the LUMO of LiPH2 is higher than the HOMO of white phosphorus. This does not make any sense, as if that were the case then this reaction would not proceed at all. It is possible that the model of LiPH2 is not very accurate, as it has been built as a covalent molecule rather than an ionic one. This may have changed the energies of the molecular orbtials enough to predict no reactivity.
A frequency analysis of red phosphorus ({http://hdl.handle.net/10042/to-1374}) was done to check that there were no negative vibrations. Since none were found, it is assumed that the minimum had been found (confirmation that the job had converged was found by consulting the log file).
White phosphorus as a ligand
White phosphorus can complex to transition metal centres as a ligand to form a transition metal complex. Two examples of this have been chosen for study; these are the bi-substituted silver and the mono-substituted rhodium complexes.
The silver complex is shown below (its optimized energy is -197.701 hartree = -519063.98 kJ/mol.
Pentahelicene |
The P4 groups have binded side-on (to give the molecule a slight tilt). The phosphorus tetrahedra have also been distorted (P-P-P bond angle is 51.996° and P-P bond length is 2.44471 Å.) The Ag-P distances are equivalent at 2.62992 Å. This shows that it the the electron density of the P-P bond that forms the interaction with the metal centre.
A vibrational analysis of the molecule was also done, this time with the expectation of seeing some IR active vibrational modes. These were indeed predicted.

| Frequency of vibration (cm-1) | Assigned vibration | IR Intensity | Expected frequency (cm-1) |
| 108.568 | Mo-ligand stretch | 110.375 | |
| 268.353 | Mo-ligand stretch | 210.274 |
The Rh complex chosen is RhCl(PPh3)2P2. This complex was only optimized twice (using the STO3G and LANL2MB basis sets) as the LANL2DZ basis set did not converge. This particular basis set was run 3 times (each time starting from the previous geometry) but the forces were still not converged. This may be important in comparing the Rh complex with the other molecules, as a less good basis set has been used the optimization will not be as good and the absolute energy value may not be exactly comparable.
Pentahelicene |
The optimized energy is given as -400.03361917 hartree = -1050288.267 kJ/mol.
The geometry of the complex is fairly odd, as it is too flat at the bottom to be a square based pyramid and is certainly not trigonal bipyramidal. The Cl-Mo-P(of P4) angle is 94.602°, P-Mo-P angle is 83.906°, the P(of PPh3)-Mo-Cl angle is 84.981°. The P-P bond length in the P4 ligand is 3.343 Å and the P-P-P angle varies between 49 and 81°.
A vibrational analysis of this complex was done. The IR spectrum obtained is shown below.

This has one strongly IR active vibrational mode at 1079.15 cm-1 with an IR intensity of 84.2644. This corresponds to a methyl vibration. It can also be seen from the vibrational analysis that the geomtery found is not a transition state, as there are no negative vibrational modes.
Conclusions
White phosphorus is reactive due to its relactively high energy HOMO (predicted by molecular orbital theroy) and the strain present in the tetrahedron. The latter cannot be predicted by MO theory, and is a limitation in the success of this project. Red phosphorus and P2 were also modelled and their energies compared with that of phosphorus. It was discovered that P2 is less thermodynamically stable than white phosphorus (explaining its low natural abundance) and red phosphorus is more thermodynamically stable (explaining why white phosphorus appears slightly yellow). White phosphorus was also investigated as a ligand, it can bind side on to silver or rhodium metal centres. This changes the bonding angles and geometry of the phosphorus tetrahedron.
References
- ↑ Literature reference used for the bond lengths and angles in the transition metal complex (the complex used was Mo(CO)4(PMe2Ph)2): DOI:10.1021/ic00131a055 10.1021/ic00131a055
- ↑ Literature reference used for the IR frequencies of the CO stretches in the transition metal complex (the complex used was Mo(CO)4(PMe2Ph)2): DOI:10.1021/ic011239z 10.1021/ic011239z
- ↑ Literature reference used for the IR data of NH3: DOI:10.1021/jp035770m
- 4. Catherine E. Housecroft and Alan G. Sharpe, Inorganic Chemistry, Third Edition, pgs 441-443