Inorganic Computational Lab:gab116
EX3 section
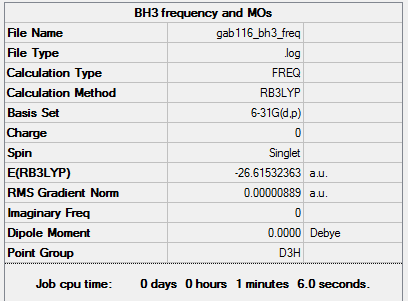
BH3
B3LYP/6-31G(d,p) level
Item Value Threshold Converged? Maximum Force 0.000018 0.000450 YES RMS Force 0.000009 0.000300 YES Maximum Displacement 0.000070 0.001800 YES RMS Displacement 0.000035 0.001200 YES
Frequency analysis log file GAB116_BH3_FREQ.LOG
Low frequencies --- -10.3498 -3.4492 -1.2454 -0.0056 0.4779 3.2165 Low frequencies --- 1162.9519 1213.1527 1213.1554
optimised BH3 molecule |
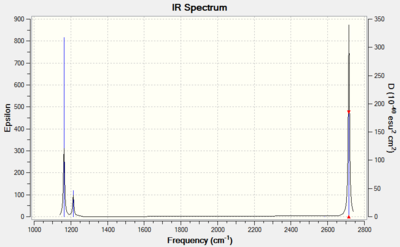
Vibrational spectrum for BH3
| wavenumber (cm-1) | Intensity (arbitrary units) | symmetry | IR active? | type |
| 1163 | 93 | A2" | yes | out-of-plane bend |
| 1213 | 14 | E' | very slight | bend |
| 1213 | 14 | E' | very slight | bend |
| 2582 | 0 | A1' | no | symmetric stretch |
| 2716 | 126 | E' | yes | asymmetric stretch |
| 2716 | 126 | E' | yes | asymmetric stretch |
|
There are fewer vibrational peaks than there are vibrations as not all vibrations are IR active, e.g. at 2582 cm-1. In addition, there are two pairs of vibrations that occur at the same wavenumber and hence overlap (at 2716 cm-1 and 1213 cm-1). As a result, there are three peaks in the spectrum even though there are six vibrations.
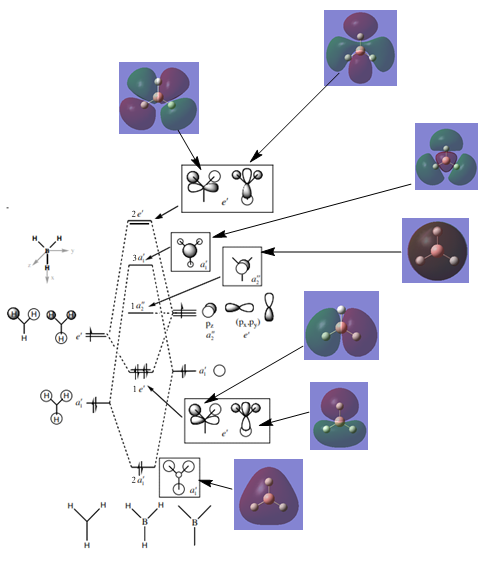
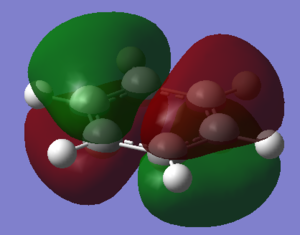
MO Diagram for BH3
Source: http://www.huntresearchgroup.org.uk/teaching/teaching_comp_lab_year2a/Tut_MO_diagram_BH3.pdf
Are there any significant differences between the real and LCAO MOs?
The real MOs are more diffuse than the LCAO MOs.
What does this say about the accuracy and usefulness of qualitative MO theory?
While qualitative MO theory is useful in terms of accurately predicting the MO's location, basic shape and relative AO contribution, it is not able to predict the volume occupied by the real MOs.
Smf115 (talk) 11:49, 28 May 2018 (BST)Clear inclusion of the calculated MOs in the diagram and nice evaluation of the useful nature of qualitative MO theory. To improve, there could have been more discussion on the similarities and differences of the calculated and qualitative MOs, for example, noticing differences in AO contirbutions particularly in the 2e' and 3a1' MOs.
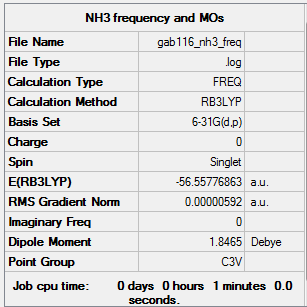
NH3
B3LYP/6-31G(d,p) level
Item Value Threshold Converged? Maximum Force 0.000013 0.000450 YES RMS Force 0.000006 0.000300 YES Maximum Displacement 0.000039 0.001800 YES RMS Displacement 0.000013 0.001200 YES
Frequency analysis log file GAB116_NH3_FREQ.LOG
Low frequencies --- -8.4661 -8.4184 -0.0028 0.0337 0.1931 26.4322 Low frequencies --- 1089.7605 1694.1862 1694.1866
optimised NH3 molecule |
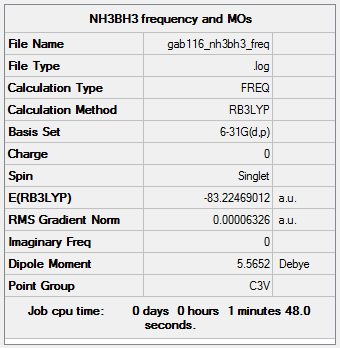
NH3BH3
B3LYP/6-31G(d,p) level
Item Value Threshold Converged? Maximum Force 0.000114 0.000450 YES RMS Force 0.000063 0.000300 YES Maximum Displacement 0.000621 0.001800 YES RMS Displacement 0.000355 0.001200 YES
Frequency analysis log file GAB116_NH3BH3_FREQ.LOG
Low frequencies --- -0.0617 -0.0457 -0.0066 21.6788 21.6848 40.5422 Low frequencies --- 266.0173 632.3610 640.1362
optimised NH3BH3 molecule |
B-N Dative Bond Energy in NH3BH3
NH3 + BH3 -> H3B:NH3
E(NH3)= -56.55777 au to 5 decimal places
E(BH3)= -26.61532 au to 5 d.p.
E(NH3BH3)= -83.22469 au to 5 d.p.
ΔE=E(NH3BH3)-[E(NH3)+E(BH3)]= -0.05160 au to 5 d.p. = -135 kJ/mol (to the nearest 1 kJ/mol)
(1.00000 au = 2625.5002 kJ/mol, source: http://www.colby.edu/chemistry/PChem/Hartree.html)
Based on your energy calculation is the B-N dative bond weak, medium or strong? What comparison have you made to come to this conclusion?
The B-N dative bond is medium strength, compared to the strong C-C bond in the similarly structured ethane and the weak intermolecular Hydrogen bond in water.
C-C bond energy= 348 kJ/mol, (source: P. Atkins and J. de Paula, Physical Chemistry, 10th Edition, 2014, OUP, 986). Hydrogen bond energy in water= 22 kJ/mol, (source: P. Atkins and J. de Paula, Physical Chemistry, 10th Edition, 2014, OUP, 674).
Smf115 (talk) 12:13, 28 May 2018 (BST)Correct calculation and nice consideration given to the accuracy of the reported energy values. Good comparisons made and referenced literature values.
BBr3
B3LYP/6-31G(d,p) LANL2DZ level
Item Value Threshold Converged? Maximum Force 0.000008 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000036 0.001800 YES RMS Displacement 0.000018 0.001200 YES
Frequency analysis log file Gab116_BBr3_FREQ_scanserver.LOG
Low frequencies --- -0.0137 -0.0064 -0.0046 2.4315 2.4315 4.8421 Low frequencies --- 155.9631 155.9651 267.7052
optimised BBr3 molecule |
Project section: Aromaticity
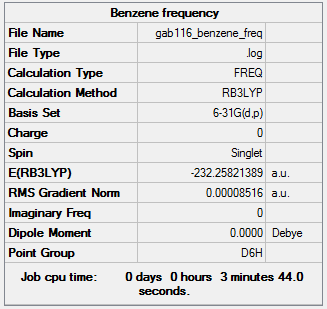
Benzene
B3LYP/6-31G(d,p) level
Item Value Threshold Converged? Maximum Force 0.000197 0.000450 YES RMS Force 0.000085 0.000300 YES Maximum Displacement 0.000780 0.001800 YES RMS Displacement 0.000333 0.001200 YES
Frequency analysis log file GAB116_BENZENE_FREQ.LOG
Low frequencies --- -3.5606 -3.5606 -0.0088 -0.0043 -0.0043 10.0905 Low frequencies --- 413.9582 413.9582 621.1416
optimised Benzene molecule |
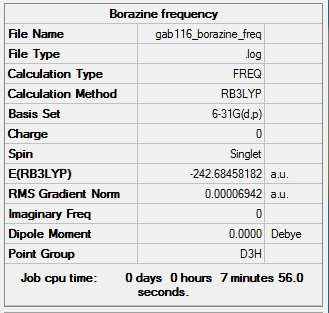
Borazine
B3LYP/6-31G(d,p) level
Item Value Threshold Converged? Maximum Force 0.000218 0.000450 YES RMS Force 0.000069 0.000300 YES Maximum Displacement 0.000332 0.001800 YES RMS Displacement 0.000106 0.001200 YES
Frequency analysis log file GAB116_BORAZINE_FREQ.LOG
Low frequencies --- -12.5959 -12.3825 -8.9170 -0.0099 0.0381 0.0783 Low frequencies --- 289.1143 289.1234 403.9108
optimised Borazine molecule |
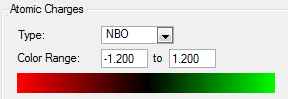
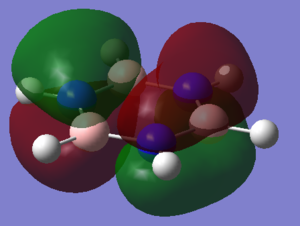
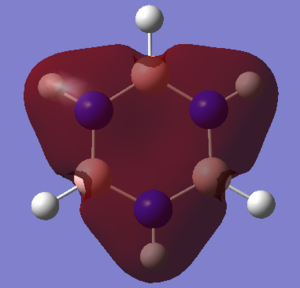
blue = nitrogen
pink = boron
NBO Charge Analysis
| Benzene | Borazine | Comparison of charge distributions |
|
|
While all components of the 6-membered ring in benzene have equal charge, the large difference in electronegativity between the boron and nitrogen in borazine means that there is an unequal distribution of charge, leading to partial ionic character. The carbons in benzene have a small relative charge of -0.239 while the hydrogens have a charge of +0.239, meaning that there is a small dipole between the carbons and hydrogens, which is due to their small difference in electronegativity. (Pauling value for carbon= 2.55, hydrogen= 2.20, source: P. Atkins and J. de Paula, Physical Chemistry, 10th Edition, 2014, OUP, 986).
In borazine, the nitrogens have a large relative charge of -1.102 and the borons have a charge of +0.747, meaning that there is a large dipole between the nitrogens and the borons. This is a result of their large difference in electronegativity. While all hydrogens on benzene have the same charge, the ones on borazine have different charges depending on whether they are connected to the negatively charged nitrogen or positively charged boron. The nitrogen connected hydrogens have a relative charge of +0.432, due to nitrogen being more electronegative than hydrogen. The boron connected hydrogens have a relative charge of -0.077, due to boron being less electronegative than hydrogen. (Pauling value for boron= 2.04, hydrogen=2.20, nitrogen= 3.04, source: P. Atkins and J. de Paula, Physical Chemistry, 10th Edition, 2014, OUP, 986). The partial ionic character and unequal distribution of charge in borazine may help to explain its higher reactivity in comparison to be benzene. |
Smf115 (talk) 11:40, 1 June 2018 (BST)Good charge analysis with the same colour range clearly used to highlight the charge distributions across both molecules. Further analysis could have considered the symmetry or the overall charges of the molecule.
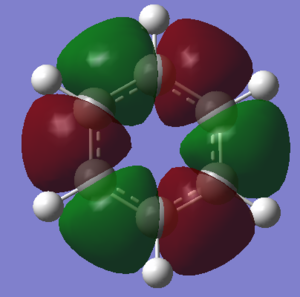
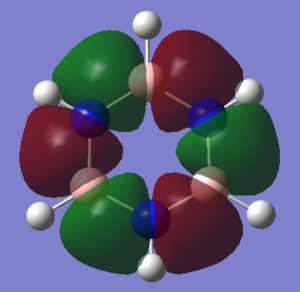
Molecular Orbital Comparison
| Benzene | Borazine | Discussion of comparative MOs |
|
|
HOMO: MO 21 (benzene) and MO 21 (borazine)
These MOs are the HOMOs and are relatively similar pi MOs. The contributing AOs are the pz orbitals perpendicular to the ring plane and there are two nodal planes; one parallel to the ring going through the atoms (characteristic of pz orbitals) and one splitting the molecule in half. The MO for borazine is less symmetric than the highly symmetric benzene MO. This is a result of the highly electronegative nitrogen atoms in borazine pulling the MO towards themselves, leading to an uneven distribution of electrons. |
|
|
MO 14 (benzene) and MO 15 (borazine)
These MOs are similar and correspond to high energy sigma bonding MOs. The contributing AOs are the px orbitals parallel to the ring plane and hence there are nodes on every atom in the ring. While the benzene MO is highly symmetric, the MOs in borazine are slightly pulled towards the nitrogen atoms due to its high electronegativity. |
|
|
MO 7 (benzene) and MO 7 (borazine)
These MOs are both low energy sigma bonding MOs and are entirely in phase with no nodes, and hence only involve s orbitals. However, the shapes aren't particularly similar. While the benzene MO is highly symmetric, the borazine MO is less so and features no contribution from the borons' hydrogen atoms. |
The Concept of Aromaticity
Aromatic systems generally have the following properties (source: https://onlinelibrary.wiley.com/doi/epdf/10.1002/chem.200700250):
1. They posses a resonance stability that mean their bond energies are more stable than their alkene equivalents and have bond lengths that are between single and double bonds.
2. When placed in an external magnetic field, a pi electron ring current is induced.
3. Aromatics are involved in reactions where the pi structure is conserved.
Simple aromatic molecules obey the empirical Hückel's rule (source: J. Clayden, N. Greeves and S. Warren, Organic Chemistry, 2nd Edition, 2012, OUP, 161); for planar compounds with a cyclic, contiguous array of p-orbitals perpendicular to the plane of the rings, there must be 4n+2 p electrons, where n is a natural number. For example, benzene is sp2 hybridized and so there are 6 pz orbitals perpendicular to the plane and 6 p electrons involved in the aromaticity and hence n=1 and Hückel's rule is obeyed.
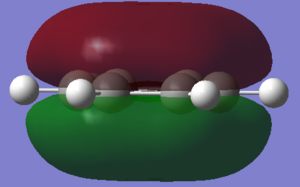
This rule leads to a simple description of aromaticity as the delocalised pi overlap of pz orbitals above and below the plane, as is shown in the image of MO 17 below.
In fact, bonding in aromatics involves a wide variety of AOs and overlaps, as can be seen from the MO comparison above. Not all aromatic MOs involve only pi orbitals and many can involve sigma interactions, including MO 7 above.
More complex interpretations of aromaticity can include sigma-only aromaticity. For example, there are main group hydride clusters that exhibit no pi aromaticity and only sigma aromaticity. σ-aromaticity and σ-antiaromaticity in saturated inorganic rings is examined in the following paper: Z.-H. Li, D. Moran, K.-N. Fan and P. von Ragué Schleyer, J. Phys. Chem. A, 2005, 109 (16), 3711–3716 (https://pubs.acs.org/doi/abs/10.1021/jp048541o).
Smf115 (talk) 11:38, 1 June 2018 (BST)Good understanding of some of the key concepts of aromaticity and reference to the MOs visualised to illustrate sigma aromaticity. To improve, the answer could have been more developed in places with a greater discussion of the properties stated, the quantitative approaches to aromaticity or around where the classical picture breaks down for example.
Smf115 (talk) 11:38, 1 June 2018 (BST)Overall , a good wiki report with a solid first section in particular.