Inorganic:whogotthefunk
Modelling Basic Molecules using Gaussian and Gaussview
Optimising a molecule of BH3
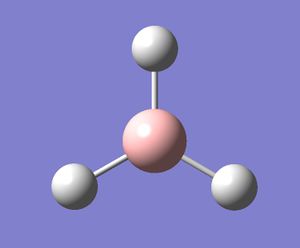

Borane (chemical formula BH3) was modelled on Gaussview. All the B-H bond lengths were set to 1.5 angstrom. It was then optimised by a Gaussian calculation, using the method B3LYP and the basis set 3-21G. As the job was small, it was not submitted to SCAN and was instead run on the laptop. This gave the molecule shown on the right (the Log file generated from this calculation is shown here: [1]).
As shown by the calculation summary shown on the right, the molecule was optimised correctly as it reached an energy minima - shown by the fact that the RMS Gradient value is very low (lower than 0.001) and is positive. The results table also shows the method and basis set that was used in the calculation, along with other properties such as the dipole moment (which is 0 in this case) and the total energy in atomic units (-26.5 for borane). The computational time for the job is also shown. As borane is so small, it only took the computer 16 seconds to optimise the molecule.
The bond angle, bond lengths and point group for borane are shown in the table below. The results showed that in the optimised molecule of borane all three B-H bonds are equivalent, both in terms of bond angle and length. The values shown in the table below are therefore applicable to all three of the B-H bonds in borane.
| B-H bond length | B-H bond angle | Point Group |
|---|---|---|
| 1.2 Angstrom | 120.0o | D3h |
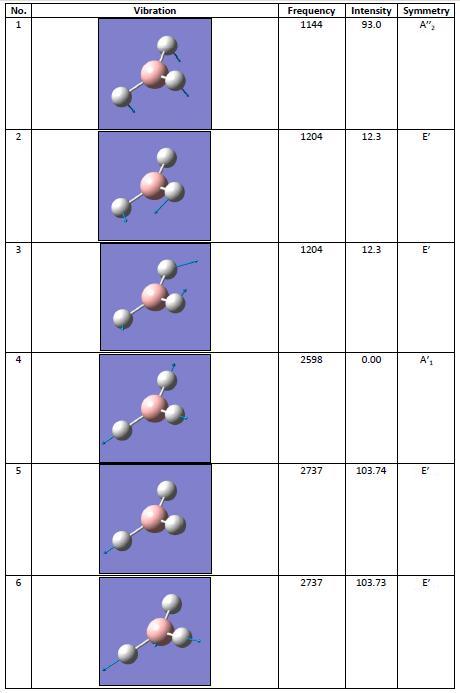
Once the molecule had been optimised, a vibrational analysis was run. This was for two reasons: to confirm that the molecule had reached a minima and therefore been optimised correctly (in more complicated molecules there is often more than one minima - this will be covered later - but in the case of BH3 the minima found in the optimisation is the lowest energy form), and to investigate the molecule's vibrations. The table of vibrations discovered from the analysis is shown in the table to the right.
From the table of vibrations it can be concluded that the molecule has reached its minima. This is because none of the frequencies are negative. If any were negative, the molecule would not have been optimised to its point of lowest energy and the calculation would have to have been be run again.
There are six frequencies of BH3, as calculated by Gaussian. However, when investigating the IR spectrum, it can be seen that it has less than six peaks. The reason for this is most likely due to degeneracy: there are two seperate vibrations at 1204cm-1, but on an IR spectrum these would be seen as one peak. The same applies to the two different vibrations that are both at 2737cm-1. There is also a zero intensity peak at 2598cm-1 - this is because there is no change in dipole moment for that particular vibration. The vibration will therefore also not be seen on the spectrum of borane.
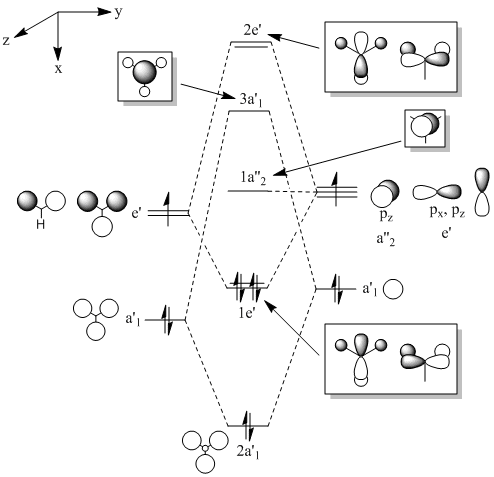
Calculating the Molcular Orbitals for a molecule of BH3
Once the molecule had been optimised, its molecular orbitals were investigated by running an MO analysis on the optimised BH3 (done by entering "pop=full" into the additional keywords section). The orbitals and the MO of BH3 are shown below. Although further orbitals for unoccupied states could have been calculated, they are not shown here, as they do not appear on the MO diagram and therefore did not need to be computationally calculated.
 |
 |
 |
 |
 |
 |
 |
Optimising a molecule of BCl3
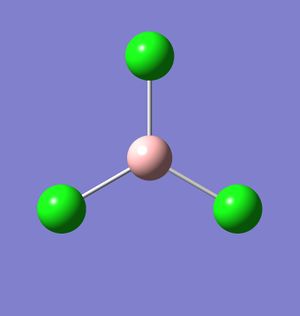
BCl3 was modelled on Gaussview using the calculation method B3-LYP and the basis set 3-21G. The same method and basis set that was used in the calculation of borane was used here because of the speed of the calculation. Although it is an inaccurate calculation due to its speed (in this case, it only took 19.0 seconds to optimise the molecule), BCl3 is a small molecule and therefore the calculations will be to a good enough degree of accuracy.
The bond angles, bond lengths and point group of BCl3 are shown below. As with borane, all three of the B-Cl bonds are equivalent, and so the data applies to all three B-Cl bonds.
| B-Cl bond length | B-Cl bond angle | Point Group |
|---|---|---|
| 1.8 Angstrom | 120.0o | D3h |
This compares favourably with the literature, which describes the molecule has having a trigonal planar shape (meaning it has a 120o bond angle) and a bond length of 175pm[1].
Gaussian optimised this molecule in four steps (i.e. it reached a minimum at the fourth configuration of the molecule). However, the first configuration did not display any bonds between the boron and chlorine atoms, which is common in Gaussview (even in some molecules where a minimum has been reached). This is because of the nature of Gaussian calculations. Gaussian calculates by taking into account molecular orbitals - how they combine and how they are positioned around each atom - and adjusts molecular positions to reach an energy minimum. This is a true representation of what bonds are - the lines Gaussview uses to link atoms are merely to show a a highly simplified version of how the molecular orbitals interact, and if the lines (bonds) are not shown in some places, it does not mean there isn't an interaction.
Cis and Trans isomerism in Molybdenum complexes
Optimisation of the Complexes
The nature of the trans and cis isomers of the compund Mo(CO4)L2 were investigated. The two ligands that define whether the molecule is cis or trans (represented by L) were here taken to be PCl3. This was to minimise calculation time as much as possible, as if the ligand was instead PPh3 - the more common ligand used in this experiment - the calculations would be far more complicated and would take much longer.
The molecules optimised in earlier calculations, such as borane, were far simpler than these Molybdenum complexes. This means that the likelihood of Gaussian finding the correct minimum for these complexes in one calculation is very small (unlike borane). This means that an initially "loose" optimisation calculation (using the calcultaion method B3LYP and the basis set LANL2MB) must be done in order to make sure that Gaussian is correctly optimising the molecule.
 |
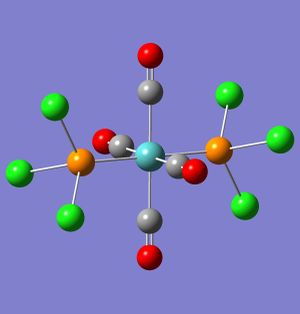 |

The results from the loose optimisations are shown above. The results are accurate, and have retained the shapes of the complexes. Despite this, the complexes must still be adjusted in order to ensure that the correct minima is reached. This is proven by the image to the right, which shows the cis complex. The full optimisation for this complex was run after making no adjustments to the loose optimisation log file, and although Gaussian reached a minimum and the calculation went to completion, the resulting complex is clearly wrong - the P-Cl bond on one of the ligands is significantly longer than any of the other P-Cl bonds in the complex. This optimised molecule is therefore wrong, and if it was used to make further calculations they would also be incorrect. This highlights the importance of not only the loose optimisation, but the examination and potential edit of it to ensure the correct minimum is reached and the optimisation is of the desired conformation.
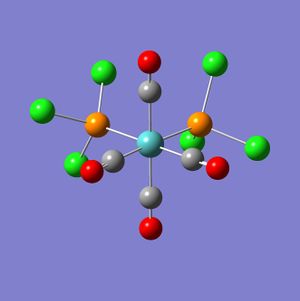
The complexes from the loose optimisation were therefore rearranged to the conformations outlined by Dr. Hunt in her instructions[2] and run again in Gaussian using a full optimisation with the calcultaion method B3LYP and the basis set LANL2DZ. The resulting complexes are shown below.
 |
 |
Incorrectly optimised Cis DOI: http://dx.doi.org/10042/to-2691 Cis DOI: http://dx.doi.org/10042/to-2690 Trans DOI: http://dx.doi.org/10042/to-2689

There is little difference between the cis and trans energies (1.2 kJ/mol). Usually the trans complex is more stable, and here it has a lower energy, showing that it is. However the energy difference between the cis and trans is so low it is not an effective measure. This is most likely due to the PCl3 ligand - in the complex the ligand is usually PPh3. PPh3 is far larger than PCl3, and as such the trans complex would be favoured as it will reduce the steric hindrance between the two PPh3 groups more than the cis complex will. This shows that it is these steric factors that decide which isomer is more favoured, rather than any electronic effects.
The bond lengths and angles compared with the literature[3] are shown below. The bond lengths are in Angstrom and the angles are in degrees.

As shown above, the resulting complexes are accurate, with similar bond lengths when the bonds are the same and correct bond angles. The computational method therefore supplies good results in agreement with the literature.
Frequency Analysis of the Complexes
Next, the complexes were run in Gaussian using the frequency calculation. The IR spectra generated are shown below.
 |
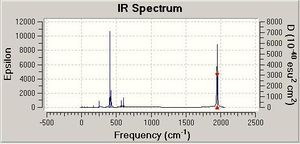 |
It is known from 2nd Year Lab that on an IR spectrum the trans isomer gives one CO peak (at around 2000cm-1) and the cis isomer gives four. Looking at the IR spectra generated, it is hard to tell whether Gaussian has predicted this correctly, so the vibrations must be looked at. These are shown in the table below.
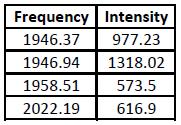 |
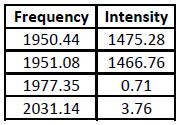 |
 |
Both isomers' data contain all four CO stretching frequencies, which does not seem to agree with the trans experimental data. However, by examining the table it is seen that two of the trans isomer's frequencies have an intensity close to zero - this means that they can be disregarded. Despite this, the trans isomer still has two peaks when it should have one. This can be explained by the fact that the trans isomer in Gaussview is not of the point group D4h (like it should be), but is instead C1, which means that there is a slight inequivalence between the CO bonds (when there isn't in the actual molecule). This causes what should be a single CO stretching frequency to become two. This can be confirmed by looking at the two frequency values - they are very similar. The values are also similar to the literature[4], showing that the calculations were carried out to a good standard.
Mini-project: Investigating the Use of 1,4-Dioxane in the Schlenk Equilibrium
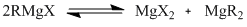
The Schlenk equilibrium, first proposed by Wilhelm Schlenk in a paper in 1929[5], is a chemical equilibrium that affects the Grignard reaction. It occurs in solutions of Grignard reagents, and results in an equilibrium between the Grginard reagent and two magnesium compounds (dihalide magnesium and dialkyl magnesium).
The Schlenk equilibrium is affected by several factors, such as solvent, the substituents on the Grignard reagent and temperature. However, the addition of 1,4-dioxane to the equilibrium leads to selective formation of the magnesium dihalide[6]. It will be investigated why this occurs, and why only a small amount of dialkyl magnesium is formed.
Determining Why the Halide Product is Favoured Over the Alkyl Product
In order to understand why the 1,4-dioxane solvated magnesium dihalide is the more favoured of the two equilibrium products, the two products were modelled on Gaussview and optimised using Gaussian. The calculation method used was B3-LYP and the basis set was LANL2DZ. Although LANL2DZ is quite a computationally intensive basis set, the molecules being modelled are fairly simple, and so computational time was still small. The magnesium dihalide used was MgCl2, and the dialkyl was MgMe2. The optimised molecules are shown below.
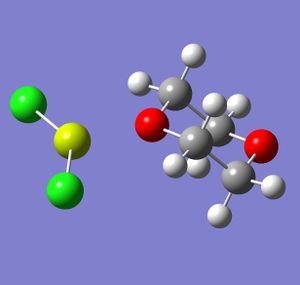 |
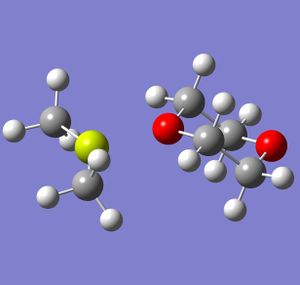 |
Chloro DOI: http://dx.doi.org/10042/to-2779 Methyl DOI: http://dx.doi.org/10042/to-2780

Several conclusions can be drawn from the data generated above. The difference in dipole moment is due to the chlorine atoms bonded to the magnesium, as they are far more electronegative than the methyl groups. The total energies show prove clearly that the halide grignard is favoured: there is an energy difference of 130577.0 kJ/mol between the two molecules, with the chloride grignard being the lower in energy. This provides computational proof that the halide grignard is the more stable and therefore more favoured equilibrium product of the two.
To understand why the halide product is more favoured, an NBO analysis must be carried out. This will generate the two molecules' orbitals, which can then be investigated. The HOMO and LUMO orbitals of each molecule are shown below.
 |
 |
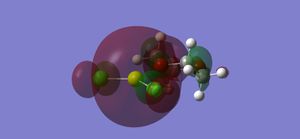 |
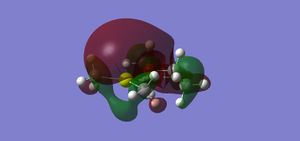 |
Chloro freq DOI: http://dx.doi.org/10042/to-2789 Methyl freq DOI: http://dx.doi.org/10042/to-2790
Analysis of these orbitals shows why the halide is favoured. Looking at the HOMO orbitals first, it is seen that the halide has a large amount of electron density on the chloride atoms, whereas the methyl's main electron density in the HOMO is at the bond between the carbon atoms and the magnesium. This shows that, as stated above, the chlorine atoms' higher electronegativity pulls electron density towards them, giving a bond in the halide of almost ionic character. The alkyl, on the other hand, has a much more covalent-type bond.
The effects of this can be seen by examining the LUMO orbitals. In the halide, the deshielded magnesium's delta-positive charge allows one of the oxygen atoms from the dioxane to fully bond with it, giving a large (bonding) molecular orbital of high electron density. This is in contrast to the alkyl, where the magnesium is not bonded as well to the oxygen atom, giving an (antibonding) orbital of lower electron density. The bond between the solvent (dioxane) and the grignard is therefore much stronger in the halide, which accounts for its higher stability. These conclusions can be confirmed by looking at some atom distances in the two compounds, shown below.

As the table shows, the halide grignard has a shorter bond from the magnesium to the oxygen. This shows that the bond is stronger in the halide than the alkyl. The length of an MgO bond (as a gaseous metal oxide) is 1.75 Angstrom[7], showing that the bond is fairly strong in the halide complex.The large orbitals of the chlorine atoms also increase the bond length between magnesium and chlorine, and increase the atomic distance between the solvent and chlorine as well.
Vibrational Analysis of the Halide and Methyl Products
Although vibrational analysis was carried out on the two compounds, it was of little use. There were no negative frequencies in either output files, showing that for both molecules, a minimum was reached and they were fully optimised. The vibrational frequencies require no real analysis for this particular project, although a shared vibration in the two molecules did show that magnesium is more delta-positive in the chloro grignard than in the methyl grignard, as shown below.
 |
 |
As shown above, the chloro grignard vibration has a higher intensity than the methyl grignard vibration at the same wavenumber. This shows that there is a greater change in dipole moment in the chloro grignard, confirming the observation that magnesium is more delta-positive in the chloro grignard. It also confirms the calculation result above that shows the chloro grignard to have a greater dipole moment.
Although they are not relevant for this project, the IR spectra of the two compounds are shown below for clarity. Most peaks in the spectra are solvent vibrations (of which there are more of in the chloro grignard compound due to the nature of the Mg-O bond), with the main difference being the large peak at 650cm-1 on the methyl IR - this peak is due to methyl group vibrations, which clearly would be absent from a halo grignard IR.
 |
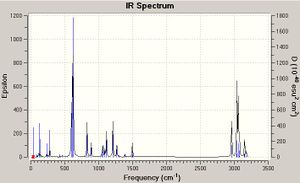 |
Determining the Most Stable Halide for Dioxane-driven Schlenk equilibrium
Halo grignards are, as shown above, the main product when the 1,4-dioxane is introduced into the Schlenk equilibrium. However, as there are several halides, analysis will be carried out to determine which is the most stable. Analysis was done using Fluorine, Chlorine, Bromine and Iodine as the halide in the halo grignard. The Gaussview models after the Gaussian optimisation calculations are shown below, along with a table showing the total energies and bond lengths.
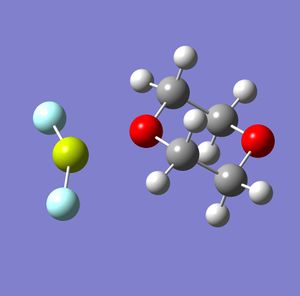 |
 |
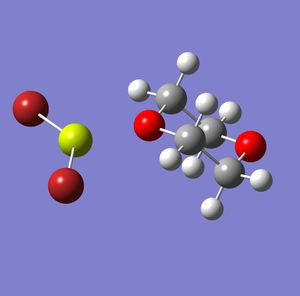 |
 |
Fluoro DOI: http://dx.doi.org/10042/to-2818 Chloro DOI: http://dx.doi.org/10042/to-2779 Bromo DOI: http://dx.doi.org/10042/to-2820 Iodo DOI: http://dx.doi.org/10042/to-2822
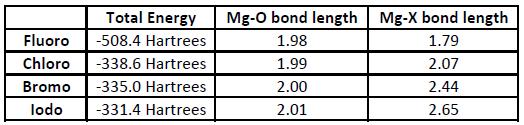
Interestingly, the most electronegative halogen - fluorine - does not give the most stable halo grignard. There is also a large difference in energy between the Fluorine and the rest of the halo grignards. This is most likely due to Fluorine's high electronegativity, which destabilises the magnesium. The iodo grignard is the most stable, and this is probably because it is still electronegative enough to make the magnesium delta-positive (and therefore form a bond with the solvent), and, as it is the least electronegative of the halogens, it destabilises magnesium the least, leading to an increased stability. Despite Iodine's large size, the molecule is not sterically crowded, and so this is unlikely to be a factor. The increase in bond lengths show that the grignards become weaker as you move down the halogen groups.
However, with most Schlenk equilibrium reactions the dihalide grignard is not needed as a product at the end of the reaction - it is instead unwanted and needs to be removed. For this, a chloro or bromo grignard is better, as they have similar energies to the iodo grignard (meaning selectivity over the alkyl grignard is maintained) but have stronger bonds. This means that the equilibrium is still driven to the right, but, instead of remaining in the mixture, the solvent-bonded halo grignard is precipitated out of the experiment, and can therefore be easily removed from the desired product.
References
- ↑ http://dx.doi.org/10.1016/S0022-328X(03)00209-2
- ↑ http://www.ch.ic.ac.uk/hunt/teaching/teaching_comp_lab_year3/10b_MoC4L2_opt.html
- ↑ http://dx.doi.org/10.1016/S0020-1693(96)05133-X Note that the literature values supplied are for a PPh3 complex.
- ↑ http://dx.doi.org/10.1021/ic50015a024
- ↑ http://dx.doi.org/10.1002/cber.19290620422
- ↑ http://dx.doi.org/10.1002/9780470132500.ch61
- ↑ J. Tossell, American Mineralogist, 65, 163
