Inorganic:ps108
Computational Module 2:Inorganic Bonding (Ab initio and density funcional molecular orbitals)
Introduction
In the following exercise Gaussview will be used as an interface with Gaussian to investigate the bonding in selected structures. BH3 and TlCl3 will be used as simple molecules to demonstrate the types of calculations that Gaussian can be used to perform. Following this Gaussian shall be used to investigate the IR spectra of the cis and trans isomers of MoCl2(CO)4. The calcualtions undertaken will have a limited accuracy due to the approximations taken in the calculations. Finally a mini-project into the electronic structure and potential bonding modes of the 1-methyl cyclopentadienyl anion and 3 isoelectronic structures where the 1-Carbon has been substituted for a Si, B and N atom, shall be undertaken using the previously investigated techniques.
Accuracy and Error Limits
All the calculations have associated with them an error that arises from the approximations used to solve the relevant equations. Therefore, in the following report it will be assumed that: 1)Energies have an error of around 10KJmol-1 = 3.808x10-3au. 2)Frequencies carry an error of 10% and shall be rounded to the nearest whole integer. 3)Intensities (also by convention) will be rounded to the nearest whole integer. 4)Bond distances have an error of 0.01A 5)Bond Angles have an error of 0.1o
Manipulation of a Molecule of BH3
A molecule of BH3 was drawn in Gaussview and all the B-H bonds were set to 1.5Angstroms. The energy was minimised using gaussian to produce an optimised structure for BH3 relative to the starting point. The had an energy of -6.94x10-4KJmol-1, with all three B-H bonds equal at 1.19349A and all the bond angle 120.000o. The effect of the optimisation calculations can be seen by the plots of energy against cycle
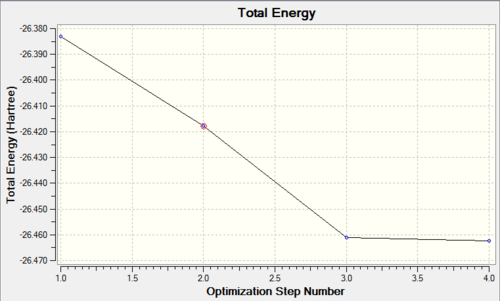
As the graph shows the energy is decreasing with each step towards a minimum point that is defined by the change in energy with each value ie. the gradient reaching a certain value. Each step corresponds to a decrease in the length of the B-H bond and can be shown using the following table:
| Step no | Step 1 | Step 2 | Step 3 | Step 4 | |
|---|---|---|---|---|---|
| image |  |
 |
 |
 | |
| B-H distance | 1.500A | 1.40834A | 1.22503A | 1.19359A |
It can be seen from the table above that only 2 of the 4 structures in Gaussian show a solid line or in other words a formal bond between the B and H atoms. This shows that Gaussview's definition of a Bond is distance dependent as opposed to the more generalised acceptance that a bond is a stabilising interaction between two atoms or molecules that leads to a new, stable state where there is a decreased distance between the bonding fragments conferring the extra stability. A plot of the RMS gradient against step number can also be used to correlate the changes in structure, in this case the change in bond length with respect to each minimisation step completed. When the change in gradient reaches 0, which occurs with step 4 the calculation has found the energy minima for the molecule with respect to the starting position and so it terminates the calculation.
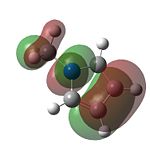
[[Image:BH3 rms gradient plot ps.png|thumb|500px|centre|The RMS gradient plot for the optimisation of BH3] -In the molecular orbitals generated by the NBO method DOI:10042/to-6514 ] the green parts denotes the parts of the molecular orbitals with positive phase and the red part resembles the part of the molecular orbital with negative phase. Following the optimisation of the molecule the molecular orbitals can be computed and were determined using an NBO analysis for a comparison the MO diagram can be graphically constructed using the LCAO approximation:
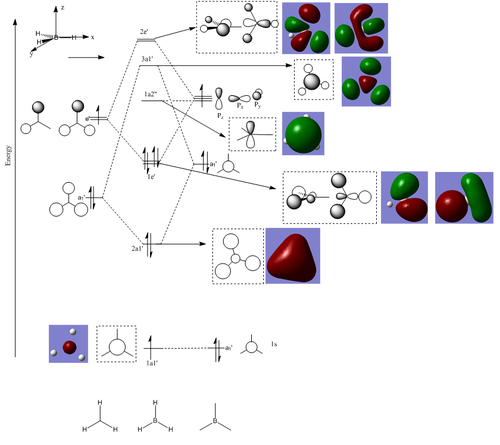
In comparing the graphically derived LCAO orbitals to the ones produced by the calculations it can be seen that the LCAO orbitals are a good representation of real life orbitals with respect to the symmetry and interactions between the orbitals. However, they fall short in describing the true distribution of electron density and overlaps between the orbitals. The relative energies of the orbitals are provided in the following table:
| Orbtial | Energy/a.u. |
|---|---|
| 1a1' | -6.8127 |
| 2a1' | -0.4760 |
| 1e' | -0.3282 |
| 1a2 | -0.08797 |
| 3a1' | 0.04379 |
| 2e' | 0.1061 |
It can be seen from the energies that the 1a1' orbital is significantly lower in energy than the other orbitals, which is due to the fact its the 1s orbital on the relatively electronegative, and so is too low in energy to interact with the orbitals of the Hydrogen atoms. Also from the calculations it can be seen that the 1a2 orbital is very close to 0au and so it can be approximated to be non-bonding as adding electrons into this orbital has a negligeable stabilising interaction on the overall molecule. The classification of the non-bonding orbital is consistent with experimental observations.
The second analysis that was performed on the BH3 molecule was an infrared analysis (output file:File:PETERSWALLOW BH3 FREQUENCY.LOG, which was calculated using the same basis sets and methods as for the NBO analysis. The results for which are highlighted in the following table
| Diagram | Description | Symmetry | Intensity | Frequency | |
|---|---|---|---|---|---|
 |
Concerted movement of the 3 H atoms in the z direction with a stationary B atom | a2 | 92.87 | 1144 | |
 |
Concerted movement of the 3 H atoms in the z direction with a stationary B atom | a2 | 92.87 | 1144 | |
 |
Stationary B atom 2 adjacent H-atoms moving in an anti-clockwise direction and the other H moving in a clockwise direction (all relative to the Z axis) | e' | 12.315 | 1204 | |
 |
Concerted movement of all 3 atoms away from the origin/B atom (which is stationary | a1' | 12.315 | 0.000 | |
 |
A push-pull type displacement of two adjacent Hydrogens ie. When one Hydrogen is moving towards the B the other is moving away and vice versa | e' | 103.74 | 2737 | |
 |
Stationary B atom, with the push-pull displacement of two adjacent Hydrogens moving away from the B centre whilst the remaining H is moving towards the centre and vice versa | e' | 103.73 | 2737 |
The spectra was also produced along with the animated vibrations
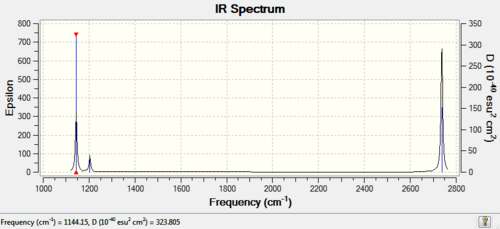
It can be seen that there are only 3 peaks in the vibrational spectrum due to the fact that there are two sets of degenerate vibrations which are found at 2737.44 and 1203.64cm-1, which means that the two peaks with the highest absorbances are a combination of the absorbancies due to these vibrations. The vibration at 2598.42cm-1 is not visualised in the Ir spectra as it is a totally symmetric vibration and so there is no overall dipole change during the vibration. This results in the vibration being forbidden with respect to the selection rules governing light absorbances, which state that there must be a change of symmetry upon absorption, and hence the vibration is IR inactive and not seen in the spectra.
TlBr3 Analysis
Given the high Toxicity of Tl and the resulting difficulty in handling it computational methods can be used to predict the properties that Tl based molecules have. This will be demonstrated using TlBr3 as an example. Like with BH3, TlBr3 was optimised using the DFT-B3LYP method, however this time the LANL2DZ basis set was used as the basis set as it provides a more accurate result than the previous method used for BH3. The results of the calculation gave an optimised energy of, with optimised bond lengths of 2.670A and a bond angle of 120o, which is a direct consequence of the molecule's symmetry being highly constrained to the D3h point group during the reaction (as the D3h point group has a C3 rotational axis each Br-Tl-Br bond angle must be exactly 120o to conform to the symmetry requirements). The bond length of 2.67A was in reasonable agreement with the experimentally recorded 2.514A [1]. The 3 main reasons for the difference between the values are the inaccuracies of the calculations, the fact the experimental length was recorded for TlBr3.4H2O and so the steric and electronic effects of the water molecules and finally crystal packing forces that occur in the solid state.
Following the optimisation of TlBr3 a frequency analysis was ran on the complex using exactly the same basis set and method. As the optimisation methods involve running calculations with respect to the first derivative, the calculations will stop when they reach a minima. However, this minima is not necessarily the most stable structure as it could be a saddle point of transitions states for the intramolecular movements being studied and so a frequency analysis is ran in order to determine whether the minimum found is the true structural minimum as the frequency is proportional to the distance between atoms and the distance is the second derivative of the molecule's energy. The crucial results of the frequency analysis involve the lowest energy vibrations of the molecule and should be zero if the molecule is at the true minimum as it would be at the bottom of the potential energy well with no movement possible. These are given by the molecules at the centre of the molecule ie. the Tl atom and are called the "low frequencies". These were found to be: -3.4213, -0.0026, -0.0004, 0.0015, 3.9362 and 3.9362cm-1, whilst these formally should be 0 and not negative in magnitude. However, the experimental error within the calculations mean that the reported values are close enough to 0 to assume that they are in fact 0 and the actual minima for the structure has been found.
The next set of frequencies termed "low frequencies" were the lowest frequencies that could theoretically be observed in an Ir spectra of the complex and this was found to be a doubly degenerate vibration at 46cm-1 and this can be seen in the Ir spectra:
The spectra can be seen to be simliar to the BH3 spectra with two regions of absorption. However, in the case of TlBr3 the first 3 IR-active vibrations are close enough in energy to overlap to form one peak. In addition to this the vibrations are shifted to lower wavenumbers going from BH3 to TlBr3, which is consistent with the B-H bond being shorted and stronger the Tl-Br. The strench of the bond is probably due to the sizes of the orbitals involved in the bonding. the Boron and Hydrogen orbitals are relatively small and not diffuse hence there is a better orbital overlap giving a stronger bonding interaction between the B and H atoms. In contrast the Br and Tl valence orbitals are very diffuse as they are larger atoms and so the valence orbitals are larger and feel a smaller effective nuclear charge. The result of the more diffuse orbitals is a worse overlap and weaker bonding interaction, which gives the weaker bond and lower vibrational frequencies.
Investigation into the Infra-Red spectra of the cis and trans isomers of a Mo(CO)4L2 Isomers
Whilst experimentally the IR spectra of Mo(CO)4L2 complexes have L=PPh3, due to the demands of the phenyl rings with respect to the calculations being ran the Ph rings were substituted for Cl atoms. The complexes were drawn in Gaussview and then optimised using the DFT-B3LYP method along with a LANL2MB basis set. Following this first optimisation the structures returned were slightly changed in Gaussian so that for the trans complex a P-Cl bond from each of the PCl3 groups eclipsed the same Mo-C bond and for the cis complex one P-Cl bond from each group eclipsed a different axial Mo-Co bond. Following this structural adjustment the minimisation was ran again this time using the DFT-B3LYP method with the LANL2-DZ basis set. The geometries were the returned and gave the following structures:
| Trans Isomer | Cis Isomer | ||||||
|---|---|---|---|---|---|---|---|
|
|
The energies of the trans and cis isomers were -623.5760au and -623.5771au, which equates to an energy difference of 2.88KJmol-1, however given that the error in the calculations is larger than the error in the calculations is greater than the energy difference between the two molecules it can't be conclusively stated that the Cis isomer is the most thermodynamically stable. In fact it has been reported in literature that the trans isomer more stable due to the steric repulsion created by putting the two PCl3 groups cis to each other compared to having them trans to each other where the distance between the groups are maximised. This effect is in part reproduced by the calculations where the Mo-P is shorter in the trans isomer compared to the cis isomer (2.45A vs 2.51A), which shows that the Mo-P bond is weaker in the cis complex and consequently, more labile in solution. The effect of the steric bulk can be invesigated by substituting the Cl atoms for larger or smaller atom eg Br of H and investigating the effect on the energy, the basis set and method must still be kept constant and so there would be the limiting factor of the calculation time on the groups that could be used. The literature P-Mo bond lengths for the trans and cis complexes were 2.500A and 2.567A respectively [2]. The magnitude of the difference between the values (0.6A) is the same for both experimental and computational methods indicating that the calculation result is reasonably accurate. The difference between the actual energies will be due to other external influences such as crystal packing forces in the solid phase. The low energy difference between the two complexes means that there is a low conversion barrier between the two isomers, a property that is very useful in catalysis as the ligand sphere of the metal can convert between the two to align with the demands of the individual catalytic steps.
A frequency analysis was then run on the optimised structures, and the lack of negative real frequencies means that the structures found are the true minimum energy structures. The frequency analysis also produced the following Ir spectra:
 |
 |
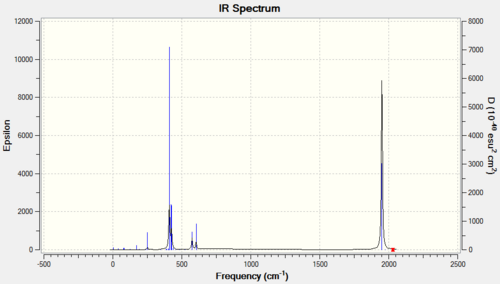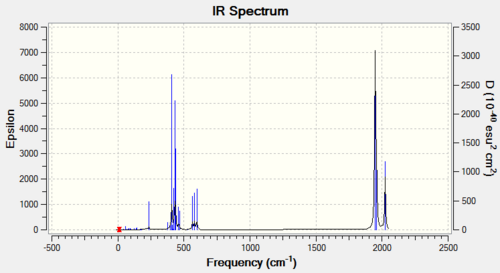It can be seen from the spectra that there is a significant difference in the carbonyl region of the Ir spectra computed is related to the symmetry of the isomers which for the cis complex is C2v and the trans isomer is D4h. Thoery predicts that a more symmetrical molecule will go a lower number of vibrationally active vibrations in the molecule as there is less chance of a dipole change that would make the vibration Ir-active. The lowest real frequencies (ie. the lowest Ir active frequencies) were found at 11cm-1and 18cm-1for the cis isomer and 5, 6cm-1 for the trans isomer. The low frequencies are all positive and so it can be concluded that the energy minima fro both structures have been found. The low frequencies all involve a twisting of the ligands demonstrating that at room temperature the groups are rotating freely about the central atom, which can be shown using 13C on a methyl-substituted phosphine would all give a single resonance. The important region of the spectra is the carbonyl region at about 2300cm-1 and both isomers have a different number of vibrations in this region. Whilst there were only two peaks in the spectrum of the cis complex there were in fact 4 Ir active vibrations occurring at 1945 (symmetry: a1), 1949(a2), 1958(b1) and 2023cm-1 (b2) therefore, there should be 4 peaks seen in the IR spectra however, due to fact the first 3 vibrations are relatively close in energy the absorptions overlap and they form 1 peak. Hence the IR spectra of the cis isomer has 2 peaks. In the trans isomer also has 4 different vibrations occuring at 1950, 1951, 1977 and 2031cm-1 However, the first two of these are degenerate (eu symmetry) as they involve the stretching of two Carbonyl ligands that are trans to each other. Hence the peaks associated with these two vibrations combine to give one single peak. The remaining two vibrations involve a very small change in the symmetry of the molecule and so have a very small dipole moment associated with them meaning they are not observed in the IR spectra and the trans Isomer has only one peak.
Mini Project: Investigation into Isoelectronic 1-Methyl Cyclopentadienyl derivatives
The use of the cyclopentadienyl anion as a ligand is well characterised (ref) due to it’s stability arising from the aromatic nature of the anion and large number of bonding interactions between the cp MOs and the metal’s orbitals. The orbitals of it’s methyl derivative will be compared to other 5 memebered rings where the carbon bound to the methyl group is substituted for a Boron, Silicon and Nitrogen atoms, with the charge being adjusted to preserve the aromaticity of the ligand. The molecular orbitals of these ligands will be generated using the DFT-B3LYP basis set and the LAN2DZ basis set, these generated orbitals will be used as a method of predicting how these ligands may react and bind to metals. A frequency analysis will be also ran on all the structures to ensure that they are the ground state structures and also provide information into the changes in the strength of the bonding.
Optimisations and frequency analysis
All of the molecules were optimised using Gaussian to give their most stable conformations. To ensure that all of the structures found were a global minima a frequency analysis on all of the compounds was ran and all apart from the Cyclopentadienyl (Cp) ring gave no negative "real" frequencies showing that the minima had been found for these complexes. For the Cyclopentadienyl structure it was noticed that one of the Hydrogens in the methyl group was in the plane of the ring, given that this is likely to be a high energy conformation it was assumed that a transition state had been found. The Methyl group was then rotated so that all of the Hydrogen atoms were pointing out of the plane of the ring and the optimisation followed by frequency analysis was re-ran and this time there was no negative frequencies showing that the global minima had now been found for this structure. The determined structures were
| Cylcopentadienyl (Cp) | Nitrogen Substituted Cp | Boron Substituted Cp | Silicon Substituted Cp | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Optimised Structure |
|
|
|
| ||||||||||||
| DOI | DOI:10042/to-6738 | DOI:10042/to-6738 | DOI:10042/to-6740 | DOI:10042/to-6739 |
It is noticable that all of the structures are totally planar apart from the structure where the 1-Carbon was substituted with a Silicon atom the methyl group is not in the plane of the ring and is in fact at an angle of 112.54o relative to the plane, suggesting that the Si is sp3 hybridised (the ideal angle for which is 109o) and therefore, the Si must have a stereochemically active lone pair. This evident lone pair suggests already that the Silicon complex will be highly nucleophilic (and basic) and will be able to co-ordinate to metals via an n1 direct sigma bonding interaction between the Silicon atom and orbitals on the metal of the correct symmetry eg the dz2 and p-orbitals.
The frequency analysis can also be used to investigate the strength of the bonding involved in these complexes: an example of the procedure used fo the frequency analysis can be demonstrated on the cyclopentadienyl ligand DOI:10042/to-6955 but applies equally to the other 3 molecules. Firstly the low, real frequencies (30cm-1) were checked and as there were no negative values and it can be assumed the true ground state of the complex had been located for subsequent analysis. Following this the vibrational spectra of the Cyclopentadienyl was produced produced was:
 |
|---|
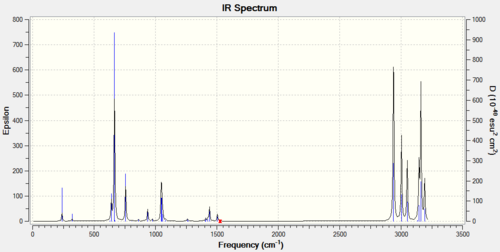The important stretches are the v(Aromatic C-H streching)= 3135-3161cm-1, v (C-C, ring breathing)=1426cm-1, and v (C-CH3)=1405 cm-1. the effect of the substitution can be seen by looking at the stretching frequency of the H3C-A stretch (A is the 1 atom that gets substituted) the results for which were 1404cm-1 C-Me; 1102cm-1 with Si-Me; 1287cm-1N-Me and 1102cm-1 for B-Me. Given that the frequency is proportional to the square root of the force constant (bond strength) divided by the reduced mass of the molecule the stability of the bonded Methyl group can be inferred from the frequencies. As Boron is lighter than Carbon it would be expected to have a lower reduced mass and hence higher vibrational frequency for the stretch However, the much lower frequency shows there is a small force constant and hence a weak bond. In comparison the Silicon and Nitrogen atoms which are heavier give a lower frequency in line with what is expected for increasing the reduced mass. The large difference would be due to a lower force constant for the bond (also an increasing mismatch in the size of the orbitals and hence a worse overlap between the orbitals).
the fact that the the Si and B substituted
NBO Analysis
The Molecular orbitals were produced using the NBO analysis using the same basis set and methods for the optimisation and frequency analysis
| Cylcopentadienyl (Cp) | Silicon Substituted Cp | Nitrogen Substituted Cp | Boron Substituted Cp | ||
|---|---|---|---|---|---|
| LUMO+2 | |||||
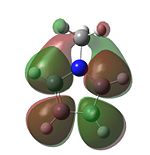
| LUMO+1 |  |
 |
 |
 |
|
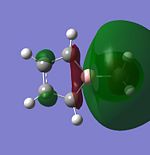
| LUMO |  |
 |
 |
 |
|
| HOMO |  |
 |
 |
 |
|
| HOMO-1 |  |
 |
 |
 |
|
| HOMO-2 |  |
 |
 |
 |
|
| HOMO-3 |  |
 |
 |
 |
General Observations on the Molecular Orbitals Generated
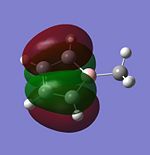
It MOs generated for the Cp and Pyrrole rings are very similar for the HOMO-2 to LUMO+1 range and this is due to the similar size of the orbitals which leads to a interactions between the surrounding orbitals which are very similar in energy. Furthermore, the electronegativities of Nitrogen and carbon are similar to each other and so the orbitals will be of similar energies. A combination of these two factors yields the similar looking molecular orbitals, with the differences arising from the electro-negativity difference giving a slightly different shape to some of the MOs. When the Carbon is substituted for the Boron (to give a Borol like molecule) the form of the MO and the energetic ordering begins to change even more. The HOMO and HOMO-1 are the same as for the Cp anion, however, the orbitals labelled HOMO-2 and HOMO-3 for Carbon swap in energetical ordering for Borol. From the MO diagram it can be seen that there is an interaction between the ring and B-CH3 sigma bond suggesting that with a less electronegative element the B-C bond is high enough in energy to mix with the pi type orbital to stabilise it. Another evident feature of the Borol type molecule is that the LUMO is almost exclusively located on the methyl substitutent which suggests that there is scope for chemistry to be carried out on the fragment possibly including acid-base reactions as the H's could be found to be more acidic than normal Methyl Hydrogens. Furthermore, it is also possible that a strong nucleophile could be used to cleave out the methyl group leading to the possibility of the molecules as a Me transfer reagent.
Finally in the Silicon Cp derivative there is a vast change in the orbitals in the HOMO-LUMO region and this is firstly due to the sp3 hybridised Silicon removing the symmetry (notably the C2 axis of symmetry) that the other 3 molecules had. Secondly Si is a large element and so has more diffuse orbitals, which are significantly higher in energy than the valence orbitals of the row two elements. Hence this leads to the different stabilising interactions and Mos observed. One of the most important features occurs of the Si derivative can be seen in the HOMO where there is a large amount of electron density located on the Si suggesting that a Si lone pair form part of the HOMO This supports the earlier suggestion that the Si was sp3 hybridised with the lone pair playing an active role in the stereochemistry of the molecule. Having the lone pair in the HOMO orbital shows that the reagent will be a strong nucleophile.
Prediction of possible bonding methods when a ligand to a transition metal
From the orbitals derived symmetry arguments can be used to predict how the molecules which orbitals can form bonding interactions with transition metal orbitals (only orbitals in the HOMO-LUMo region will be considered). From these symmetry matches the bonding mode nx where x denotes the number of Carbons bonding to the metal. Taking the pure cyclopentadienyl anion as an example:
 |
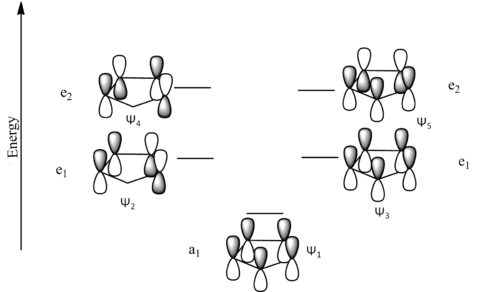In the maximised bonding state (n5): The lowest energy (a1) ligand MO can form bonding interactions with the pz, s and dz2 (for the latter the metal is important as there is a nodal cone in the dz2 which would limit the bonding interactions depending on how diffuse the orbitals are) metal orbitals.
The first of the e1 orbitals (w2) can form bonding interactions with the px and dxz orbitals,
The second e1 orbital (w3) can form bonding interactions with the py and dyz orbitals,
The first e2 orbital (w4) can form a bonding interaction with the dxy orbtial
Finally the second e2 orbital (w4) can form a bonding interaction with the dx2-y2 orbital
Furthermore, it is important to note that n3 and n1 bonding can occur between orbitals of the relevant symmetry The orbitals created in this way can be compared to the calculated orbitals where it can be seen that the HOMO-2 is the a1 orbital, the HOMO-1 is the e1 (w2) orbital and the HOMO is the e1 (w3) orbital. In the cyclopentadienyl anion MO diagram these are degenerate orbitals, but methyl fragment splits this degeneracy as one of it's orbitals has an anti-bonding interaction with the w3 orbital increasing it in energy. As w2 has no electron density on the methyl fragment at all, the orbital is relatively stabilised. It can be seen that the e2 (w4) orbital matches up nicely with the LUMO but the LUMO+1 doesn't take the form expected of it from the LCAO prediction and it can be seen that this is again due to the role of the methyl group which in the case of this orbital the molecular orbital is almost totally on the methyl fragment. Therefore, it can be assumed that methyl based MO has slotted in between the e2 orbitals and that w5 is found at a higher energy.
Assuming that the energy levels of the metal are of the appropriate level for interacting with the ligand orbitals (which can only be shown by calculating the whole complex)the same symmetry treatment to the calculated MOs and the interactions with transition metals can be described:
| Molecule | HOMO-3 | HOMO-2 | HOMO-1 | HOMO | LUMO | LUMO+1 | |
|---|---|---|---|---|---|---|---|
| Cyclopentadienyl | can have an n2 type interaction between the pi symmetry part of the orbital on C3-C4 and the metal's p or d orbitals of appropriate symmetry ie(to pz or dz2) | Can form a n5 interaction with the dz2, pz and s orbitals or a n2 interaction with the d-orbitals of appropriate symmetry | can form an n5 interaction with appropriate p and d orbitals as well as a n2 interaction with appropriate d-orbitals | can form an n5 interaction with appropriate p and d orbitals as well as a n2 interaction with appropriate d-orbitals | n2 interaction between the part of the MO on C3-C4 and d-orbitals of relevant symmetry | The LUMO+1 appears to be non-bonding as there doesn't seem to be any suitable symmetry matches however, further calculation would be needed to prove this as a very weak sigma bonding interaction could occur with the part of the molecular orbital on C3-C4 giving an n2 type interaction | |
| Nitrogen Derivative | can form a n2 interaction with the dz2 orbital when the C3-C4 bond is parallel to the metals z-axis | Can form a n5 interaction with the dz2, pz and s orbitals or a n2 interaction with the d-orbitals of appropriate symmetry and a n2 interaction with the dxy orbital | can form an n5 interaction with the d orbtials of appropriate symmetry as well as an n2 interaction with a d or p orbital of appropriate symmetry | n5 interaction with d-orbitals of appropriate symmetry | n2 bonding with d and p orbitals of relevant symmetry | appears to be non-bonding with respect to symmetry arguments | |
| Boron Derivative | Can form a n5 interaction with the dz2, pz and s orbitals or a n2 interaction with the d-orbitals of appropriate symmetry | can form a n2 (pi) interaction with the p-orbitals appropriate symmetry | can form a n5 bonding interaction between p and d-orbitals of appropriate symmetry | can form a n5 and n2 bonding interaction between p and d-orbitals of appropriate symmetry | can form an n1 interaction with the pz, dz2 and s orbitals | can form a n5 interaction with p and d-obitals of appropriate symmetry. | |
| Silicon Derivative | appears to be non-bonding through symmetry arguments although it is possible n1 and n2 modes could occur. | can form a pi bond (n2 interaction) at the C3-C-4 end of the molecule with p-orbitals of appropriate symmetry | n5 interaction possible with d or p orbitals of appropriate symmetry | can form an n1 interaction with the pz, dz2 and s orbitals or n2 with the d and p orbitals of relevant symmetry | can form n2 bonding at C3-C4 end of the molecule and n1 bonding to the Silicon with dz2 of pz orbitals to form a Si-M bond | can form n1 or n2 (at the C3-C4 end) although this would be substantially weaker) with d and p orbitals of relevant symmetry. |
It is important to note once again that the above has been derived from symmetry only considerations and that energetics will play a very important role in defining which orbitals interact. Furthermore, often "p or d-orbitals of appropriate symmetry" has been used as there will also be steric constraints, especially given the the methyl group, imposed by other ligands on the orientation of the studied molecules relative to the metal centre which will define the exact orbitals that interact. Examples of the interactions are given below:
| Pyrrole HOMO-3 | Cp HOMO-2 | Cp HOMO-1 | Silicon HOMO | |
|---|---|---|---|---|
 |
 |
 |
 |
|
| The dz2 orbital seems have a good overlap with the portion of the molecular orbital about the C3-C4 | It can be seen that interaction between the pz orbital and the C3-C4 end of the Cp ligand can form a bonding interaction with pseudo pi type symmetry in an n2 bonding interaction | The p-orbtial superimposed onto the face of the ligand orbital shows how the n5 bonding interaction could occur | The s-orbital has the potential to overlap well with the lone pair on the Silicon atom to form the n1 bonding interaction |
All of the molecules show potential to bond via both the n2 and n5 modes under the right steric conditions. The exact bonding mode will depend on the electron density of the metal (ie. how highly oxidised it is, the co-ligands and whether it is an early -electron deficient- or late -electron rich- transition metal) the effect of which can be demonstrated by taking the Pyrrole unit. For electron deficient metal, the stabilising (bonding interactions arise from electron density on the Ligand being donated into empty orbitals on the metal. However, exact predictions into the most stable state would take more rigorous analysis with the metal orbitals being included in the analysis as the energetic and steric contributions to the stability of the complex are just important as symmetry matching the orbitals. Unfortunately there was not enough time to run this full analysis and so this is an area which could be expanded on in future work. However, from the interactions previously described suggests that all of the molecules can bond to metal centres via both the n5 and n2 modes, with n1 binding possible with the orbitals lower in energy and is favoured by more ionic bonding and hence hasn't been discussed. However, the n1 bonding would be very stable between the Silicon derivative and electron deficient metals as the lone pair can donate into the appropriate metal orbitals to form a relatively strong covalent bond.
Using a Full basis set instead of the pseudo-potential
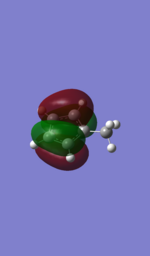
The LAN2DZ basis set that was used to produce all of the MOs gave generally good orbitals that agreed reasonably well with the LCAO derived approximations. However, the lower level of accuracy imparted by this basis set meant that there was the possibility of using a full basis set (the 6-31G basis set) to produce the MOs and see if there was any siginificant difference given by using the two methods. Therefore, the NBO analysis was re-ran for the methyl-cyclopentadienyl ligand and this gave the following molecular orbitals (with original calculated ones for reference):
| Basis set used | HOMO-3 | HOMO-2 | HOMO-1 | HOMO | LUMO | LUMO+1 | |
|---|---|---|---|---|---|---|---|
| 6-31G |  |
 |
 |
 |
 |
 |
|
| LAN2DZ | |
|
|
|
|
|
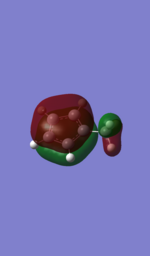
It can be seen that the bonding orbitals produced by the methods shows very similar shapes and therefore, in this region there was little difference in the results produced by the basis sets. However, it can be seen that the shapes of the LUMO and LUMO+1 orbitals are the opposite to each other, whilst the two different methods used means that the exact orbital energies compared by evaluating the bonding and anti-bonding regions of the Molecular orbitals the energy differences can be rationalised. The reason for the different ordering can be seen by evaluating the 6-31G LUMO and comparing it to the LAN2DZ LUMO+1, which are very similar in shape however there are two key differences which influence the energetic ordering of the LUMO and LUMO+1 orbitals. Firstly the contribution to the molecular orbital by the C3 and C4 carbons is lower when the 6-31G basis set is used, as the interaction in this region is anti-bonding (shown by a node) the smaller orbitals reduce the anti-bonding interaction and lower the energy of the 6-31G orbital relative to the one produced by the LAN2DZ. Secondly the phase of the molecular orbital on the Hydrogens at the C2 and C5 carbon (the ortho Hs) is the opposite, the result of which is for the 6-31G there is a bonding interaction with the methyl fragment, which is shown by the component of the orbtials being de-localised over the two Hydrogens and the methyl fragment. In contrast the opposite phase in the LAN2DZ produced orbital means that there is an anti-bonding interaction between the methyl fragments and the ortho Hs which means that it would be higher in energy relative to the 6-31G produced orbitals.
Furthemore, it can be seen that the methyl fragment has a higher contribution to the LUMO+1 in the 6-31G relative to the LUMO in the LAN2DZ method and in fact has 2 nodal planes about the methyl fragment relative to the latter's 1 meaning that it would be higher in energy that the same MO produced by the LAN2DZ method. The result of this combined with the evaluation of the other orbtial means that the ordering of the LUMO and LUMO+1 has been reversed with changing the basis set.
It appears from the above discussion that the LAN2DZ was a reasonable basis set to undertake the mini project as the orbitals are of very similar shape and in general the same ordering. However the approximations taken in the pseudo basis set means that some of the more subtle components of the orbitals were not calculated correctly. Therefore, it can be concluded that the LAN2DZ basis set (for which the calculations ran very effeciently) is a good basis set to use if the approximate shape of an orbital is required, however, the higher level basis sets would be needed if a detailed investigation into the shape and form of the molecular orbitals was going to be undertake.
Conclusion
From the analysis of the electronic structure the possible bonding methods for the substituted Cyclopentadieneyl ligands have been calculated and the possible bonding methods which transition metals were extracted from symmetrical arguments and it could be seen that all the molecules have the potential for multiple bonding modes with a metal centre meaning that they would all be useful as ligands in catalysis as they can slip between the binding modes to accommodate the differing needs of the metal at the different steps in the catalytic cycle. It was found that by replacing the pseudo-potential basis set with the full basis set there was a considerable increase in the time taken for the calculation to run despite being a small molecule without giving vastly different results. However, the ability of the higher basis set to give more information into the subtle parts of the molecular orbital was also demonstrated.
---