IMM: AC5116
Introduction
The purpose of this lab was to learn how to use the software Gaussian to model molecules.
Ammonia, NH3
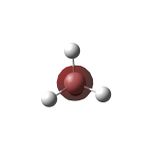
A molecule of ammonia was created in Gaussview 5.0 ADD REFERENCE and initially set to have NH bond lengths of 1.3 angstrom and the HNH bond angle was set to 109.471°.
Optimisation
A OPTF optimisation calculation was ran using the B3LYP method (the approximations made) with the 6-31G(d,p) basis set (this determines the calculation accuracy, in this case a medium accuracy). The point group was C3v.
"Item Table" (Found in the Gaussian output .log File, which can be found here.)
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000072 0.001800 YES
RMS Displacement 0.000035 0.001200 YES
Predicted change in Energy=-5.986283D-10
Optimization completed.
-- Stationary point found.
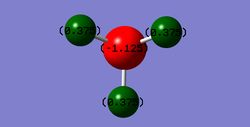
Forces are quoted in au and the displacements(from the saddle point) in UNITS. The optimised geometry of this NH3 molecule was calculated to have an NH bond length of 1.01798 angstrom and a HNH bond angle of 105.741 °. The energy of this structure was calculated as E(RB3LYP)=-56.55776873 au and the RMS gradient was 0.00000485 au. The partial charges on the atoms are expected to be negative on N and positive on H, owing to the greater electronegativity of nitrogen compared to hydrogen; the optimisation calculation supports this (with nitrogen having a charge of 1.125 and with each H having a charge of +0.375).
Optimised Structure of Ammonia |
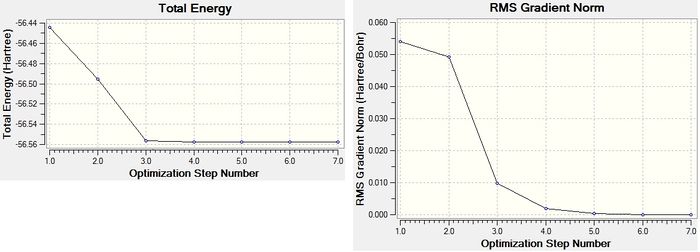
The actual calculation of the optimised structure is an iterative process that finds the nearest local minimum of the molecules potential surface, where dE/dr=0(where r is a given co-ordinate being varied). Each intermediate step has a different energy (and corresponding structure) that approaches the minimum energy.
Vibrational Spectra
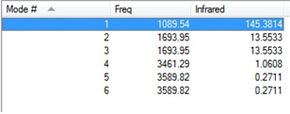
Using an OPTF calculation in Gaussian also calculates the frequencies of NH3 fundamental vibrational modes and the corresponding intensities expected in an infrared spectra. 6 vibrational modes were calculated, this corresponds with the 3N-6 (3*4-6=6) vibrational modes expected of ammonia.
| Header 1 | Frequency/ cm-1 | IR Intensity(Nearest Int.) | Vibration |
|---|---|---|---|
| 1 | 1089.54 | 145 | "Umbrella" Symmetric Bend |
| 2 | 1693.95 | 14 | Asymmetric Stretches |
| 3 | 1693.95 | 14 | Asymmetric Stretches |
| 4 | 3461.29 | 1 | Symmetric Stretch- All bonds stretch equal amounts |
| 5 | 3589.82 | 0 | Asymmetric stretches |
| 6 | 3589.82 | 0 | Asymmetric stretches |
The Gaussview software can display animations of these vibrational modes, as in the image to the left. The table above shows that NH3 has 2 pairs of degenerate vibrational modes (same vibrational frequencies and hence energy), at the 3589.82 cm-1 and 1693.95 cm-1, corresponding to asymmetric stretches and bends, respectively. The 3rd mode is highly symmetric due to all 3 N-H bonds stretching equally and in phase.The IR intensity of the last 2 vibrational modes is very low, signifying these vibrational modes are largely IR inactive; have no or low change in dipole moment.
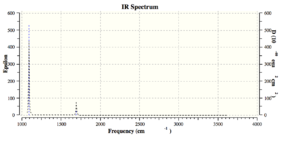
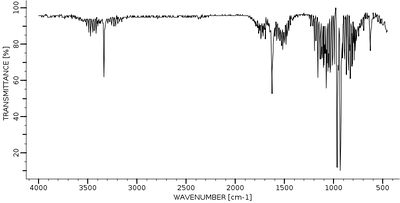
An experimental IR spectra from Bio-Rad Laboratories [1] can be seen below. A notable difference between the two spectra is that the experimental spectrum has 3 intense peaks whereas the calculated spectrum has only 2. This seems to be due to the peak at 3461.29 cm-1 having a relative calculated IR intensity much lower than should be expected, and hence doesn't appear in the Gaussview spectra. It is also possible that the extra experimental peak at ~3400 cm-1 is due to some form of experimental impurity such as a solvent, but it is unlikely as ammonia is a gas.
Hydrogen
Optimisation
A OPTF optimisation calculation was ran using the B3LYP method (the approximations made) with the 6-31G(d,p) basis set (this determines the calculation accuracy, in this case a medium accuracy). The point group was Dh,.
"Item Table" (Found in the Gaussian output .log File, which can be found here.)
(Linear) (Quad) (Total)
R1 1.40369 0.00000 0.00000 -0.00001 -0.00001 1.40368
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000005 0.001800 YES
RMS Displacement 0.000007 0.001200 YES
Predicted change in Energy=-1.939322D-11
Optimization completed.
-- Stationary point found.
Forces are quoted in au and the displacements(from the saddle point) in UNITS. The optimised geometry of this H2 molecule was calculated to have an H bond length of 0.74280 angstrom. No bond angle is requied to define the H-H connectivity as it is diatomic. The energy of this structure was calculated as E(RB3LYP)= -1.17853936 au and the RMS gradient was 0.00000222 au. This energy is significantly higher (i.e. less negative) than that of ammonia, due to the formation of fewer bonds. The partial charges on the atoms are both zero as expected, due to being a homonuclear diatomic molecule.
Optimised Structure of Hydrogen |
The actual calculation of the optimised structure is an iterative process that finds the nearest local minimum of the molecules potential surface, where dE/dr=0(where r is a given co-ordinate being varied). Each intermediate step has a different energy (and corresponding structure) that approaches the minimum energy. This was completed in 4 steps, a fair few less than what was required to calculate the optimum structure of NH3, perhaps due to the greater simplicity of a hydrogen molecule and that only one internal co-ordinate (the H-H bond length) needs to be optimised.
As the Energy gradient(net force) reaches zero, it can be taken as the optimisation of H2 structure was completed.
Vibrations
Very little can be said about the calculated IR vibrations for H2. Only one mode was calculated, matching the expectation that hydrogen has 3N-5 (3*2-5=1) vibrational modes, at 4465.60 cm-1. This mode is a symmetric stretch and is IR inactive due to molecular hydrogen being a homonuclear diatomic and hence absorption of radiation will result in a Transitional Dipole moment of 0.
Nitrogen, N2
Optimisation
A OPTF optimisation calculation was ran using the B3LYP method (the approximations made) with the 6-31G(d,p) basis set (this determines the calculation accuracy, in this case a medium accuracy). The point group was Dh,.
"Item Table" (Found in the Gaussian output .log File, which can be found here.)
R1 2.08909 0.00000 0.00000 0.00000 0.00000 2.08909
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Predicted change in Energy=-1.647237D-14
Optimization completed.
-- Stationary point found.
Forces are quoted in au. The optimised geometry of this N2 molecule was calculated to have an NN bond length of 1.10550 angstrom. No bond angle is required to define the NN connectivity as it is diatomic. The energy of this structure was calculated as E(RB3LYP)= -109.52412868 au and the RMS gradient was 0.00000013 au. This energy is significantly more negative than that of ammonia and hydrogen, owing to nitrogen's extremely strong NN triple bonds. The partial charges on the atoms are both zero as expected, due to being a homonuclear diatomic molecule.
Optimised Structure of Nitrogen |
The actual calculation of the optimised structure is an iterative process that finds the nearest local minimum of the molecules potential surface, where dE/dr=0(where r is a given co-ordinate being varied). Each intermediate step has a different energy (and corresponding structure) that approaches the minimum energy. This was completed in 4 steps, a fair few less than what was required to calculate the optimum structure of NH3, perhaps due to the greater simplicity of a nitrogen molecule and that only one internal co-ordinate (the N-N bond length) needs to be optimised.
As the Energy gradient(net force) reaches approximately zero, it can be taken as the optimisation of N2 structure was completed.
Vibrations
Very little can be said about the calculated IR vibrations for N2. Only one mode was calculated, matching the expectation that nitrogen has 3N-5 (3*2-5=1) vibrational modes, at 2457.33 cm-1. This mode is a symmetric stretch and is IR inactive due to molecular hydrogen being a homonuclear diatomic and hence absorption of radiation will result in a Transitional Dipole moment of 0. This frequency is lower than in hydrogen due to the far heavier nitrogen atoms, despite nitrogen's stronger triple bond.
Molecular Orbitals
Nitrogen has 2 occupied π bonding MOs, that are degenarate, but no occupied π* anti-bonding MOs. There is also one filled σ bonding orbital, made from the overlap of 2 2p orbitals along the bonding axis, but the corresponding σ* orbital is empty. Hence, nitrogen has a bond order of 3.
The Harber-Bosch Process
The Harber-Bosch process is a method of generating ammonia under high pressures and reasonable temperatures, for use in the production of fertilisers, first developed by Fritz Haber in 1910 [2]
The reaction taking place is:
Calculating the energy difference, between the reactants and the products of this reaction, and converting from atomic units to kJ mol-1 using a online converter [3], can be used as an approximation for the change in internal energy, , of the reaction. As the Haber process occurs under fixed pressures and volumes, it is reasonable to assume that .
Determining the Energy of Reaction
| -56.55776873 a.u. | |
| -113.11553746 a.u. | |
| -109.52412868 a.u. | |
| -1.17853936 a.u. | |
| -3.53561808 a.u. | |
| -0.0557907 a.u. | |
| in kJ mol-1 | -146.478494 kJ mol-1 |
Hence the energy change of the reaction is calculated as= -146.48 kJmol-1. This has the expected sign that literature values of have e.g. (= -92.22 kJ mol-1 [4] from 2* enthalpy of formation of ammonia ), indicating that the products (2 equivalents of ammonia) are more thermodynamically stable than the reactants (3 equivalents of H2 and 1 of N2). The calculated value is significantly more negative than the literature value. This is likely due to the fact that the calculated is calculated from the energy of lone molecules at 0 K and hence doesn't account for inter-molecular interactions and the rotational and translational energies of the individual molecules- it'd be very difficult to determine exactly the reason by behind this difference, particularly at this level. Another very important factor is just that this energy is NOT the enthalpy change and only an approximation.
Optimisation and Orbital Calculation of a Borohydride Anion, BH4-
The same procedure used for N2, H2 and NH3 was used to determine the optimum structure of BH4- and it's orbitals.
Results of Structure Optimisation
BH4-'s optimised structure was calculated using the RB3LYP method with the 6-31G(d,p) basis set, as with the other calculations presented in this wiki page. The point group of the optimised structure is Td.
Energy
The final optimised energy of the borohydride anion was calculated to be -27.24992701 a.u. with an RMS gradient of 0.00000671 a.u., indicating the optimisation was complete and a minima energy was found. Supporting the finding of a minima is the lack of any imaginary frequencies (see next section), confirming that the second derivative of the energy (used as an approximation of the force constant of the bonds for calculating the vibrational frequency of the normal modes) was greater than 0 and hence the -27.25 a.u. energy was found at a minimum.
"Item Table" (Found in the Gaussian output .log File, which can be found here.)
Item Value Threshold Converged? Maximum Force 0.097394 0.000450 NO RMS Force 0.052059 0.000300 NO Maximum Displacement 0.150000 0.001800 NO RMS Displacement 0.080178 0.001200 NO Predicted change in Energy=-4.168257D-02
Structure
The minimised structure had a tetrahedral shape( and hence a Td point group, as each of the 4 atoms surrounding the central boron atom are the same). Each of the 4 B-H bonds have an identical length of 1.23933 angstrom. All the HBH bond angles are 109.471 degrees.
Optimised Structure of the Borohydride anion |
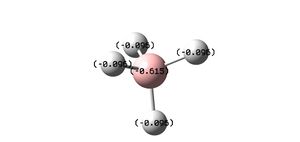
The partial charges on each atom in the above figure make sense. Despite boron having approximately the same electonegativity as hydrogen, the BH4- molecule has a negative charge, so you can't treat the charge on each atom as 0. Formally, this charge resides on the boron atom, as it lacks a complete octet. The calculated charge is less than -1, however as the Hydrogen atoms have slightly higher electro-negativity than the boron atom, so some of the charge is dispersed over those atoms too.
Vibrational modes of BH4- =
The IR vibrational modes of BH4- were calculated as follows
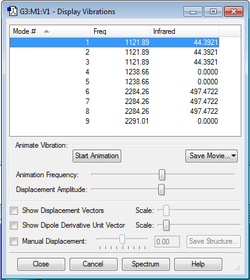
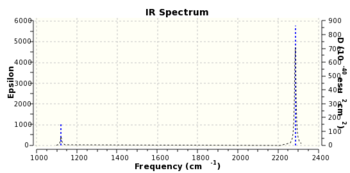
There are 3 sets of degenerate modes of vibration for this molecule:1-3, 4+5 and 6-8. Modes 1-3 are Symmetric "Umbrella" bends and are IR active, vibrations 4 and 5 are IR inactive Asymmetric bends, 6,7 and 8 are very IR active asymmetric stretches, 9 is a symmetric stretch that, is IR inactive due to the tetrahedral shape of BH4- being symmetrical, hence resulting in no change in dipole moment of the molecule. Similar symmetry effects cause result in the other IR inactive modes having a Transitional Dipole moment of 0. BH4- having 9 vibrational modes is consistent with the 3N-6 rule.
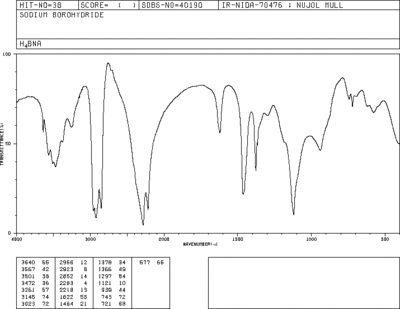
The IR spectra generated by gaussview has 2 peaks, one at 2284 cm-1 and another minor one at 1121 cm-1. Both of these peaks are present in the spectra obtained from the AIST Spectral Database For Organic Compounds(SDBS) [5], among several other peaks- likely due to solvent or the nujol used. Bizarrely the 1121 cm-1 from the SDBS has a similar intensity to the 2284cm-1 peak, whereas in the predicted spectra the 1121 peak is far smaller.
Molecular Orbitals of BH4- =
The molecular orbitals of BH4- determined using the RB3LYP method are depicted in the table below:
| Number | MO Image | Description |
|---|---|---|
| 1 | 
|
This orbital is just the B 1s orbital. Due to being so tightly bound(and far lower in energy than any other orbital (-6.42128 a.u. opposed to -0.222587 a.u. for orbital 2) there is not overlap between the hydrogen s orbitals. This is occupied with a pair of electrons. |
| 2 | 
|
This orbital is constructed from the Boron 2s orbital and the 4 hydrogen 1s orbitals in phase. E= -0.222587 a.u. This orbital is fully occupied by a pair of electrons. This orbital surrounds the tetrahedral shape of the borohydride anion closely, and hence is likely responsible for the tetrahedral shape of the anion. This orbital is responsible for some of the BH bonding. |
| 3,4,5 |   
|
These 3 orbitals are degenerate with E= -0.03183 a.u. and are made up from a boron p orbital with each lobe overlapping in phase with 2 hydrogen 1s orbitals, forming these jelly bean like structures. These orbitals strangely point between the tetrahedral hydrogens, but the lobes cover them. These could be responsible for 3 of the 4 B-H bonds, however surprisingly they are not sigma orbitals that point along the bond axis, but more like pi orbitals.
The fact that the 4 BH bonds can be attributed to 2 different energies of orbitals is surprising, considering all 4 bond lengths are equal. This is either an indication that the no one orbital can be attributed to a single bond, but really all 4 orbitals contribute to BH4- each bond partially. |
| 6,7,8 |   
|
These 3 degenerate orbitals are unoccupied(the LUMOs), with a positive energy of +0.41617 a.u. . They are the corresponding anti bonding orbitals to orbitals 3,4 and 5, made up from the same orbitals as them. |
| 9 | 
|
This anti-bonding orbital is constructed from the Boron 2s orbital and the 4 hydrogen 1s orbitals out of phase. This MO is the opposite of orbital 2. It is formed by the out of phase overlap of the boron 2s and the 4 hydrogen 1s atomic orbitals. This orbitals energy is +0.43601 a.u.. |
Reactivity of BH4-
In curly arrow mechanisms of reduction of carbonyls to alcohols with NaBH4- a B-H bond is shown as breaking and a new C-H bond forming. This results in the formation of BH3 (borane) and an alkoxide intermediate, that gets protonated to form the alcohol product. The breaking of the B-H bond suggests that the HOMO of borohydride is some form of sigma bonding orbital along one of the BH bonds; this is not the case, the HOMOs (as seen in the previous section) are 3 degenerate orbitals of energy that point in between two BH bonds. This further supports the idea mentioned in the previous section that a given bond in borohydride does not have 1 corresponding MO, like in simpler systems such as N2, though could be described as such using VB theory, though hybrids of the 4 bonding MOs in borohydride should point along the tetrahedral bonds. After one of these HOMO's are emptied in a nucleophillic attack, the 3 remaining H's and the boron atom rearrange to give borane.
MO's of BH3
Boranes energy was calculated in attempt to calcluate the energy chagne of the above reaction, however due to time constraints wasn't completed and only the optimisation and orbitals are shown.
Method: RB3LYP
Basis Set:6-31G(d,p)
Energy: -26.61532364 au
RMS Gradient:0.00000211 au
Point group: D3h
IR:
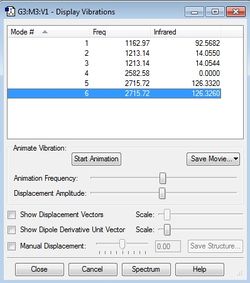
Log File: here
Item Table: "Item Table" (Found in the Gaussian output .log File, which can be found here.)
Item Value Threshold Converged? Maximum Force 0.006105 0.000450 NO RMS Force 0.003997 0.000300 NO Maximum Displacement 0.023278 0.001800 NO RMS Displacement 0.015239 0.001200 NO Predicted change in Energy=-2.135202D-04
| Orbital | Description |
|---|---|
|
B 2s, 3*H 1s |
 ,
|
2 bonding orbitals made from B 2p and 3*H 1s |
| P-orbital | One remaining P-orbital from boron, essentially without overlap with any other orbital. Out of plane of the planar borane molecule. |
References
- ↑ 1.0 1.1 From Bio-Rad Laboratories, found on Sci finder. https://scifinder.cas.org/scifinder/spectral/retrieveImage?id=BR164587&source&type=IR&display=IR+Absorption+Spectrum&hires=false
- ↑ https://en.wikipedia.org/wiki/Haber_process
- ↑ http://www.colby.edu/chemistry/PChem/Hartree.html
- ↑ Atkins and De Paula, Physical Chemistry 10th Edition, page 977
- ↑ 5.0 5.1 The AIST Spectral Database for Organic Compunds, http://sdbs.db.aist.go.jp/sdbs/cgi-bin/direct_frame_top.cgi