IMM2 Hans Chan 01196664

Background

This investigation focuses on finding the optimised structure of molecules using quantum mechanical simulations. Optimisation was achieved by using the software Gaussian. In this workbook the results from optimisation of various molecules are reported. The following are included for each molecule;

Key information about the calculation,
Results.
Item Table,
Rotatable 3D jmol file and image of the optimised structure,
Link to the final file of the optimisation or frequency.

Non-interactive images of relevant molecules were generated using Gaussview.

Molecular Modelling

Ammonia NH₃

Ammonia

Optimisation

The following settings were used for the optimisation of this molecule(click link for the .log file);

Calculation Type	Calculation Method	Basis Set
FREQ	RB3LYP	6-31G(d,p)

The following results were generated;

Final Energy E(RB3LYP) /a.u.	RMS Gradient /a.u.	Symmetry
-56.55776870	0.00004995	C_3v

The item table here shows that the structure has converged;

         Item               Value     Threshold  Converged?
 Maximum Force            0.000080     0.000450     YES
 RMS     Force            0.000053     0.000300     YES
 Maximum Displacement     0.000235     0.001800     YES
 RMS     Displacement     0.000117     0.001200     YES

Geometry

The molecule takes a trigonal pyramidal geometry. As the hydrogen atoms are in an identical chemical environment, they have identical bond angles and bond lengths. The bond angle and bond length are shown in the table below;

Geometry
N-H Length /Å	H-N-H Angle /°
1.01808	105.736

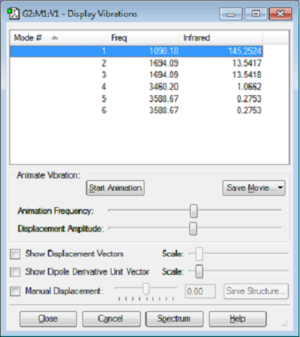
Vibrational Modes

The vibrational modes of the molecule are shown in the table below;

Vibrational Modes
Mode	Freq /Hz	IR
1	1090.18	145.2524
2	1694.09	13.5417
3	1694.09	13.5417
4	3460.20	1.0662
5	3588.67	0.2753
6	3588.67	0.2753

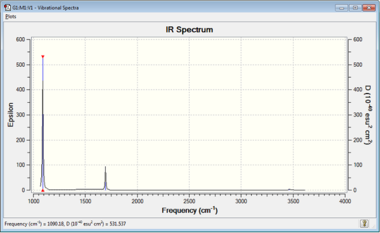
The above information was extracted from Gaussian's 'Vibrations' function (Figure 1).

From the 3N-6 rule 6 modes of vibration are expected in ammonia (N=4). This is consistent with what was calculated.
Modes 2 and 3 (scissoring bends) and 5 and 6 (asymmetric stretches) are degenerate pairs as they have the same energy associated to them.
Modes 1 to 3 corresponds to bends, and modes 4 to 6 corresponds to stretches.
Mode 4 is highly symmetric.
Mode 1 is a symmetric bend and is otherwise known as the 'umbrella' mode.
In an experimental spectra of gaseous ammonia, 4 bands should be expected. All the vibrational modes are associated with a change in dipole moment of the molecule , hence these oscillations are all IR active.^[1] However the degenerate pairs of vibrational modes correspond to the same frequency as given by $E = h f$ , where $f$ is the frequency and $h$ is the Planck's constant.

Note that Gaussian predicts a spectra with apparently two bands instead of four (Figure 2). This is because modes 4 and 5-6 are significantly weaker in comparison with the other three modes. Close observation shows that Gaussian displays them as a very weak peak around 3500cm^-1.

Charges

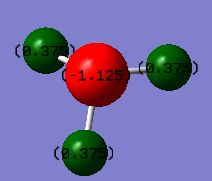
The relative charge distributions on the atoms as calculated by Gaussain are shown below;

Relative Charge
N	H
-1.125	0.375

The charges on the atoms computed by Gaussian are as expected; Due to the relative electronegativity of nitrogen in comparison with hydrogen (nitrogen 3.04 and hydrogen 2.20 on the Pauling Scale),^[2] the assigned relative charge on nitrogen is negative (Figure 3). The sum of the charges on all atoms give zero, which is consistent physically as the molecule has no overall charge.

Hydrogen H₂

Hydrogen

Optimisation

The following settings were used for the optimisation of this molecule(click link for the .log file);

Calculation Type	Calculation Method	Basis Set
FREQ	RB3LYP	6-31G(d,p)

The following results were generated;

Final Energy E(RB3LYP) /a.u.	RMS Gradient /a.u.	Symmetry
-1.17853936	0.00000017	D_∞h

The item table here shows that the structure has converged;

         Item               Value     Threshold  Converged?
 Maximum Force            0.000000     0.000450     YES
 RMS     Force            0.000000     0.000300     YES
 Maximum Displacement     0.000000     0.001800     YES
 RMS     Displacement     0.000001     0.001200     YES

Geometry

The molecule is linear. The bond angle and bond length are shown in the table below;

Geometry
H-H Length /Å	H-H Angle /°
0.60000	180

Vibrational Modes

The vibrational mode of the molecule is shown below;

Vibrational Modes
Mode	Freq /Hz	IR
1	4465.58	0.0000

As it is a diatomic molecule the only vibrational mode is a stretch. No overall change in dipole moment renders the molecule IR inactive, as predicted by Gaussian.

Nitrogen N₂

Nitrogen

Optimisation

The following settings were used for the optimisation of this molecule(click link for the .log file);

Calculation Type	Calculation Method	Basis Set
FREQ	RB3LYP	6-31G(d,p)

The following results were generated;

Final Energy E(RB3LYP) /a.u.	RMS Gradient /a.u.	Symmetry
-109.52412868	0.00000079	D_∞h

The item table here shows that the structure has converged;

         Item               Value     Threshold  Converged?
 Maximum Force            0.000001     0.000450     YES
 RMS     Force            0.000001     0.000300     YES
 Maximum Displacement     0.000000     0.001800     YES
 RMS     Displacement     0.000001     0.001200     YES

Geometry

The molecule is linear. The bond angle and bond length are shown in the table below;

Geometry
N-N Length /Å	N-N Angle /°
1.10550	180

Vibrational Modes

The vibrational mode of the molecule is shown below;

Vibrational Modes
Mode	Freq /Hz	IR
1	2457.33	0.0000

As it is a diatomic molecule the only vibrational mode is a stretch. No overall change in dipole moment renders the molecule IR inactive, as predicted by Gaussian. Note that the vibration frequency of the nitrogen molecule is lower. The vibrational angular frequency is given by $ω = \sqrt{k / μ}$ , where $k$ is the bond spring constant and $μ$ is the system's reduced mass. Although nitrogen has a stronger bond (a larger $k$ ), the much lighter hydrogen molecule give an appreciably smaller reduced mass, resulting in a higher vibrational frequency.

Reaction Energy Consideration - Bosch-Haber Process

The Bosch-Haber Process converts nitrogen and hydrogen gas into ammonia;

N₂ + 3 H₂ → 2 NH₃

The energy change of the reaction can be predicted using the energies of the molecules as calculated by Gaussian. The following table summarises the energies of the molecules computed above.

Energy /a.u.
E(NH₃)	E(N₂)	E(H₂)
-56.55776870	-109.52412868	-1.17853936

The total energy change of the process is thus;

ΔE = 2 × E(NH₃) - [ E(N₂) + 3 × E(H₂) ]

= 2 × -56.55776870 - [ -109.52412868 + 3 × -1.17853936 ]

= -113.1155374 - [ -109.52412868 + -3.53561808 ]

= -0.05579064 a.u. = -146.478 kJ·mol⁻¹.

A negative solution shows that the reaction is exothermic, and the sum of energies of the product is lower than the sum of energies of the reactants. This products are hence more stable than the reactants. The solution is by no means accurate compared to an empirical value of −91.88kJ·mol^-1 under standard conditions. ^[3] This can be attributed to the fact that computational calculations do not take reaction conditions into account.

Silanone H₂SiO

Silanone

Note that silanone is also the general name assigned to the silicon analogues of ketones. Here the silicon equivalent of formaldehyde is concerned.

Optimisation

The following settings were used for the optimisation of this molecule(click link for the .log file);

Calculation Type	Calculation Method	Basis Set
FREQ	RB3LYP	6-31G(d,p)

The following results were generated;

Final Energy E(RB3LYP) /a.u.	RMS Gradient /a.u.	Symmetry
-365.90001403	0.00000941	C_2v

The item table here shows that the structure has converged;

         Item               Value     Threshold  Converged?
 Maximum Force            0.000023     0.000450     YES
 RMS     Force            0.000009     0.000300     YES
 Maximum Displacement     0.000023     0.001800     YES
 RMS     Displacement     0.000017     0.001200     YES

Geometry

The molecule is roughly trigonal planar around the central silicon. The bond angles and bond lengths are shown in the table below;

Geometry
Si=O Length /Å	Si-H Length /Å	H-Si=O Angles /°	H-Si-H Angle /°
1.53172	1.48652	124.156	111.686

It can be seen that the H-Si=O angle and the H-Si-H angle are not exactly 120°, which would be the case if the molecule was indeed trigonal planar. This is a result of the higher electron density in the Si=O double bond repelling the Si-H single bonds.

Vibrational Modes

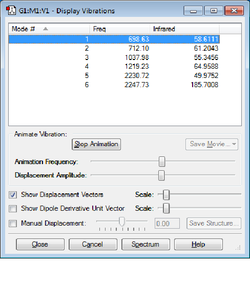
The vibrational modes of the molecule is shown below;

Vibrational Modes
Mode	Freq /Hz	IR	Type
1	698.63	58.6111	Bending (Wagging)
2	712.10	61.2043	Bending (Rocking)
3	1037.98	55.3456	Bending (Scissoring)
4	1219.23	64.9588	Scissoring Bend and Stretch
5	2230.72	49.9752	Symmetric Stretch
6	2247.73	185.7008	Asymmetric Stretch

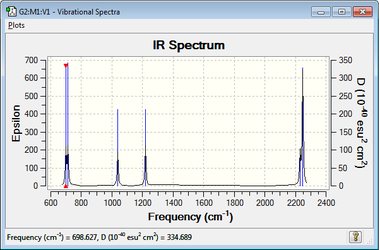
All of the above are associated with a change in dipole moment in silanone and are therefore IR active. None of the modes are degenerate so six distinct vibrational frequencies are expected (Figure 5). The wide peaks at both ends of the spectrum are two unresolved peaks - the low frequency 'doublet' corresponds to Modes 1 and 2 and the peak at around 2200cm^-1 are Modes 5 and 6.

Charges

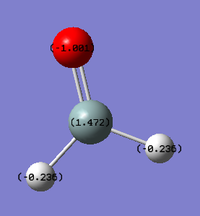
The relative charge distributions on the atoms as calculated by Gaussain are shown below;

Relative Charge
Si	H	O
1.472	-1.001	-0.236

The sum of the charges is again zero, which is consistent theoretically as the molecule has no overall charge (Figure 6). Oxygen is, relative to the other atoms, the most electronegative (3.44 on the Pauling Scale) and is thus assigned the most negative charge value. Silicon has the lowest electronegativity (1.9 on the Pauling Scale)^[2] and has a positive charge distribution. The hydrogen atoms have an electronegativity between the two, accounting for the charge distribution.

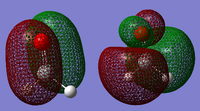
Molecular Orbitals

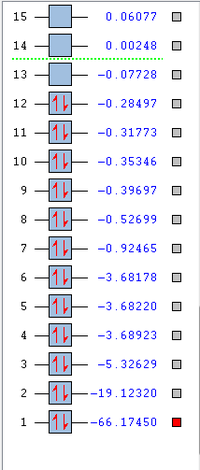
The electronic energy levels of the molecule is shown in Figure 7. The following are some of the molecular orbitals of silanone;

Energy Level	Surface	Description
1-3		These are the core s-electrons from the silicon and oxygen atom. E(1) cannot be seen on Gaussview because it is hidden within the atom. These electrons do not contribute too much to the overall MO. The oribtals shown on the left are the 2s electrons from both atoms.
4-6		These are the 2p orbitals from the silicon core. These do not contribute a lot to the MO either.
7		Orbital 7 contribute to some form of σ-bond between silicon and oxygen. The absence of a different phase on the smaller node is of interest; the silicon is expected to be sp² hybridised, which should generate a smaller green node on the opposite side of the silicon atom. This could be a result of further integration of AO's between the hydrogen atoms and silicon.
8,10		E(8) seems to be the σ-bonds joining the hydrogen atoms to the silicon. E(10) is possibly the corresponding σ* orbital. When joined together however they do not completely cancel as expected in an occupied bond-antibond MO pair; the node on the Si-H σ-bonds remain. It is possible that these two combine to give the σ-bonds between silicon and hydrogen.
9,12		E(9) is some form of extended π-bond in the whole molecule. It is in the plane of the trigonal molecule, as opposed to being vertical in a conventional π-bond. E(12), the HOMO, appears to be the complimentary π-antibond. As both orbitals are occupied, it might be in agreement with the fact that this bond is not predicted in Valence Bond theory.
11,13		E(11) is a π-bond between the silicon and the oxygen. The unoccupied E(13) is the complimentary π*-antibond, and also the LUMO.

Detailed knowledge of fragment point groups should allow better analysis.

Reaction Energy Consideration - Silanone Synthesis

The following process converts ethylene oxide and silylene into silanone and ethene in SF₆ bath gas;^[4]

H₄C₂O + H₂Si → H₂SiO + H₄C₂

The energy change of the reaction can be predicted using the energies of the molecules as calculated by Gaussian. The following table summarises the energies of the molecules computed in Gaussian.

Energy /a.u.
E(H₄C₂O)	E(H₂Si)	E(H₂SiO)	E(H₄C₂)
-153.79194941	-290.61526271	-365.90001403	-78.59380796

Relevant .log files:

The total energy change of the process is thus;

ΔE = [ E(H₄C₂) + E(H₂SiO) ] - [ E(H₂Si) + E(H₄C₂O) ]

= ( -78.59380796 - 365.90001403 ) - ( -290.61526271 - 153.79194941 )

= -0.08660987 a.u. = -227.394 kJ·mol⁻¹

The first calculations used to predict this reaction, executed at the MP2 and QCISD levels of theory using 6-31G basis, gave a value of -61.8kcal·mol⁻¹, or -258.57kJ·mol⁻¹.^[5] Both suggest a highly exothermic reaction, however without an experimental value for comparison no conclusions can be drawn.

References

↑ P. Atkins and J. de Paula, Atkins' Physical Chemistry, Tenth Edition, 2014, 416.
↑ ^2.0 ^2.1 J.E. Huheey, E.A. Keiter, and R.L. Keiter, Inorganic Chemistry : Principles of Structure and Reactivity, 4th edition, HarperCollins,1993.
↑ K. T. Klemola, Chem. Eng. Ed., 48 (2), 2014, 115–120.
↑ R. Becerra, J. P. Cannady, O. Goulder, R. Walsh, J. Phys. Chem. A, 114 (2), 2010, 784–793.
↑ Y. Apeloig, S. Sklenak, Can. J. Chem., (78), 2000, 1496–1510.

[Atkins-1] P. Atkins and J. de Paula, Atkins' Physical Chemistry, Tenth Edition, 2014, 416.

[electronegativity-2] 2.0 ^2.1 J.E. Huheey, E.A. Keiter, and R.L. Keiter, Inorganic Chemistry : Principles of Structure and Reactivity, 4th edition, HarperCollins,1993.

[Haber-Bosch-3] K. T. Klemola, Chem. Eng. Ed., 48 (2), 2014, 115–120.

[Silanone-4] R. Becerra, J. P. Cannady, O. Goulder, R. Walsh, J. Phys. Chem. A, 114 (2), 2010, 784–793.

[Silanone2000-5] Y. Apeloig, S. Sklenak, Can. J. Chem., (78), 2000, 1496–1510.

[1]

[2]

[3]

[4]

[5]

Background

Molecular Modelling

Ammonia NH3

Optimisation

Geometry

Vibrational Modes

Charges

Hydrogen H2

Optimisation

Geometry

Vibrational Modes

Nitrogen N2

Optimisation

Geometry

Vibrational Modes

Reaction Energy Consideration - Bosch-Haber Process

Silanone H2SiO

Optimisation

Geometry

Vibrational Modes

Charges

Molecular Orbitals

Reaction Energy Consideration - Silanone Synthesis

References

Ammonia NH₃

Hydrogen H₂

Nitrogen N₂

Silanone H₂SiO