IMM2 : Jae Eun Lee CID : 01076523
NH3 molecule
Optimisation of NH3 molecule
Key information about NH3 molecule
Molecule Name : Ammonia(NH3)
Calculation method : RB3LYP
Basis set : 6-31G(d.p)
Final energy E(RB3LYP) in atomic units (au) : -56.55776873
RMS gradient in atomic units (au) : 0.00000323
The point group of the molecule : C3V
N-H bond distance = 1.01798 Å
H-N-H bond angle = 105.745 °
Item table of NH3 molecule
The optimisation file is linked to here
Item Value Threshold Converged?
Maximum Force 0.000006 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000014 0.001800 YES
RMS Displacement 0.000009 0.001200 YES
Predicted change in Energy=-1.141685D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.018 -DE/DX = 0.0 !
! R2 R(1,3) 1.018 -DE/DX = 0.0 !
! R3 R(1,4) 1.018 -DE/DX = 0.0 !
! A1 A(2,1,3) 105.7446 -DE/DX = 0.0 !
! A2 A(2,1,4) 105.7446 -DE/DX = 0.0 !
! A3 A(3,1,4) 105.7446 -DE/DX = 0.0 !
! D1 D(2,1,4,3) -111.8637 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
Table 1. Item table of NH3 molecule
The table above shows that the energy of the NH3 molecule is the minimum and therefore the structure of the NH3 is optimised.
Jmol dynamic image of NH3 molecule
Figure 1. NH3 Molecule at the lowest energy state CID : 01076523 |
Animating the Vibrations
Image of display vibrations of NH3 molecule
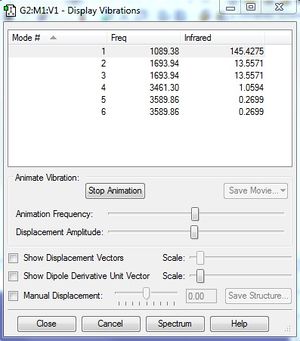
Q&A
Q1 : How many modes do you expect from the 3N-6 rule?
A : Number of modes = 3(4) - 6 = 6 modes.
Q2 : Which modes are degenerate?
A : mode 2 and 3 (frequency = 1693.94 cm-1), and mode 5 and 6 (frequency = 3589.86 cm-1) are degenerate.
Q3 : Which modes are 'bending' vibrations and which are 'bond stretch' vibrations?
A : mode 1, 2 and 3 are bending vibrations and mode 4, 5 and 6 are bond stretch vibrations.
Q4 : Which mode is highly symmetric?
A : Mode 4 is highly symmetric (symmetric stretching of N-H bond).
Q5 : One mode is known as the 'umbrella' mode, which one is this?
A : Mode 1 is known as the 'umbrella' mode (symmetric bending of N-H bond).
Q6 : How many bands would you expect to see in an experimental spectrum of gaseous ammonia?
A : There are two peaks in the experimental spectrum of gaseous ammonia. The intensity of the peaks is dependent on the change of the dipole moment of the molecule. The intensity of the peak of mode 1 is much higher than other modes because the symmetric bending vibrations lead to a large change of dipole moment. However, the other modes have much smaller change of dipole moment and this leads to lower intensity of the peaks. Mode 2 and 3 have less symmetric bending vibrations and this minimizes the change in dipole moment. The stretching vibrations of mode 4, 5 and 6 lead to insignificant change in dipole moment and therefore the intensities of the peaks are insignificant such that they not observable on the spectrum.
Charge Analysis
Charge of the N-atom : - 1.125
Charge of the H-atom : + 0.375
Expectation of the charges of the N and H atoms :
The charge of the N atom would be negative and the charge of the H atom would be positive. It is because the N atom is more electronegative than the H atom. Since NH3 is a neutral atom the sum of the charges is equal to 0.
Reactivity
H2 molecule
Key information about H2 molecule
Molecule Name : Hydrogen molecule(H2)
Calculation method : RB3LYP
Basis set : 6-31G(d.p)
Final energy E(RB3LYP) in atomic units (au) : -1.17853936
RMS gradient in atomic units (au) : 0.00000017
The point group of the molecule : D∞H
Item table of H2 molecule
The optimisation file is linked to here
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000001 0.001200 YES
Predicted change in Energy=-1.164080D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 0.7428 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
Table 2. Item table of H2 molecule
The table above shows that the energy of the H2 molecule is the minimum and therefore the structure of the H2 is optimised.
Jmol dynamic image of NH3 molecule
Figure 3. H2 Molecule CID : 01076523 |
Image of display vibrations of H2 molecule
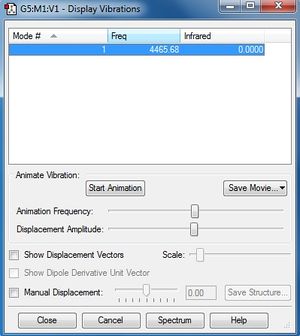
frequency : 4465.68 cm-1
There is only one frequency because a diatomic molecule has only one mode of vibration.
The intensity of the H2 molecule is zero because there is no dipole moment for the H2 molecule.
N2 molecule
Key information about N2 molecule
Molecule Name : Nitrogen molecule(N2)
Calculation method : RB3LYP
Basis set : 6-31G(d.p)
Final energy E(RB3LYP) in atomic units (au) : -109.52412868
RMS gradient in atomic units (au) : 0.00000060
The point group of the molecule : D∞H
Item table of N2 molecule
The optimisation file is linked to here
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Predicted change in Energy=-3.401007D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1055 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
RMS Displacement 0.000000 0.001200 YES
Table 3. Item table of N2 molecule
The table above shows that the energy of the N2 molecule is the minimum and therefore the structure of the N2 is optimised.
Jmol dynamic image of N2 molecule
Figure 5. N2 Molecule CID : 01076523 |
Image of display vibrations of N2 molecule

frequency : 2457.33 cm-1
There is only one frequency because a diatomic molecule has only one mode of vibration.
The intensity of the peak of the N2 molecule is zero because there is no dipole moment for the stretching vibration of the N2 molecule.
Calculating the energy of the reaction
E(NH3) = -56.55776873 au
2*(NH3) = -113.11553746 au
E(N2) = -109.52412868 au
E(H2) = -1.17853936 au
3*E(H2) = - 3.53561808 au
ΔE = 2*(NH3)-[E(N2)+3*E(H2)] = -0.0557907 au
By converting the energy difference into KJ/mol,
ΔE = -0.0557907 * 2625.5 = -146.47848285 KJ/mol = -146.48 KJ/mol.
Q : Identify whether the gaseous reactants are more stable or the ammonia product is more stable.
A : The ammonia product is more stable than the gaseous reactants because the energy is released when the ammonia product is formed. Thus, the ammonia product has lower energy compared to the gaseous reactants. Therefore the ammonia product is more stable.
Choosing my own molecule : HCl
Key information about HCl molecule
Molecule Name : Hydrogen Chloride molecule(HCl)
Calculation method : RB3LYP
Basis set : 6-31G(d.p)
Final energy E(RB3LYP) in atomic units (au) : -460.80077875
RMS gradient in atomic units (au) : 0.00005211
The point group of the molecule : C∞V
Item table of HCl molecule
The optimisation file is linked to here
Item Value Threshold Converged?
Maximum Force 0.000090 0.000450 YES
RMS Force 0.000090 0.000300 YES
Maximum Displacement 0.000139 0.001800 YES
RMS Displacement 0.000197 0.001200 YES
Predicted change in Energy=-1.256951D-08
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.286 -DE/DX = 0.0001 !
--------------------------------------------------------------------------------
Table 4. Item table of HCl molecule
The table above shows that the energy of the HCl molecule is the minimum and therefore the structure of the HCl is optimised.
Jmol dynamic image of HCl molecule
Figure 7. HCl Molecule at the lowest energy state CID : 01076523 |
Vibrations of N2 molecule
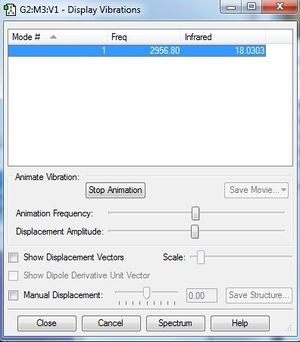
Analysis
HCl has 1 mode of vibration based on the calculation below.
Number of modes = 3N - 5 = 3(2)- 5 = 1 mode.
Diatomic molecules such as HCl have only one mode of vibration because only stretching vibration is possible for linear diatomic molecules.
Based on Figure 8, the stretching vibration of HCl molecule has the absorption frequency at 2956.80 cm-1.
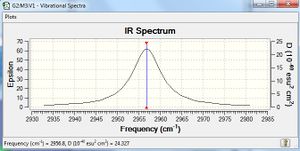
Figure 9 shows the IR spectrum of the HCl molecule. It has only one peak because it has only one stretching vibration at 2956.80 cm-1. The broad absorption band is observed due to the hydrogen bonding formed between the HCl molecules. The extent of hydrogen bonding between HCl molecules varies in the sample and as a result, IR absorption occurs at slightly different frequencies. Different extents of absorption broaden the peak of the HCl molecule in the IR spectrum.
Unlike N2 and H2 molecules, HCl has a dipole moment due to different electronegativities of H atom and Cl atom. Thus, the peak is observed.
Comparing with the literature value
The literature value of the frequency of the HCl peak is 2990.946 cm-1. Since the frequency determined by using Gaussview is 2956.80 cm-1, the value is accurate.
Atomic charges of HCl
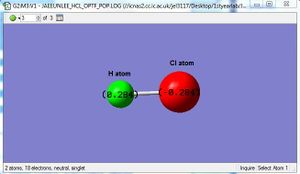
Analysis
The charge on the H atom is positive while the charge on the Cl atom is negative because the Cl atom is more electronegative compared to the H atom. Since HCl is a neutral molecule, the sum of the charges of the H and Cl atom is equal to zero.
Molecular Orbitals of HCl molecule
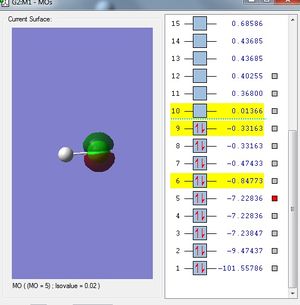
Analysis
The inner 1s, 2s and 2p orbitals of Cl atom do not interact with 1s orbital of H atom because they are tightly bounded to the nucleus of Cl atom. As a result, they remain as non-bonding orbitals in HCl molecular orbital. Since they are tightly bounded, they have much lower energies than 3s and 3p orbitals.
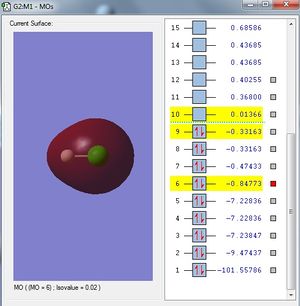
Analysis
3s orbital of Cl atom is large enough to interact with 1s orbital of H atom. In this case, both 1s orbital of H and 3s orbital of Cl are in-phase such that they have a constructive overlap of orbitals to form a bonding orbital.
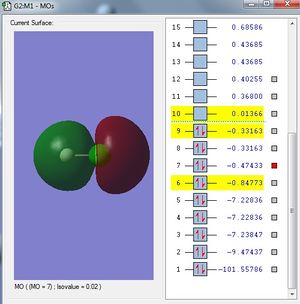
Analysis
In this case, the 1s orbital of H atom is out of phase and the 3pz orbital of Cl atom is in the right orientation and phase to interact with the out of phase H atom. Thus, it forms the sigma bond.
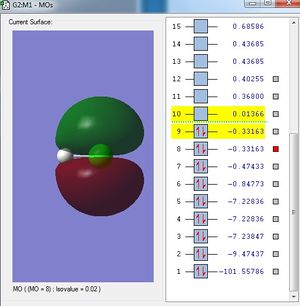
Analysis
The 3px and 3py orbitals are orientated in such a way that they are not able to overlap with 1s orbital of the H atom. Thus, those 3p orbitals remain as non-bonding molecular orbitals.
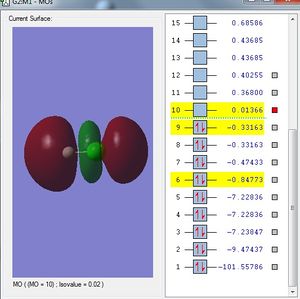
Analysis
In this case, the 1s orbital of H atom is in-phase but the side of 3pz orbital that overlaps with the 1s orbital of the H atom is out of phase. As a result it forms an anti-bonding molecular orbital.
