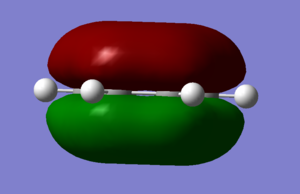
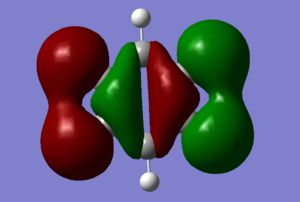
ICC2 01053372
EX3 Section
BH3
Method & Basis Set
RB3LYP
6-31G(d,p)
Summary Table
Item Table
Item Value Threshold Converged?
Maximum Force 0.000006 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000022 0.001800 YES
RMS Displacement 0.000015 0.001200 YES
Predicted change in Energy=-1.868217D-10
Optimization completed.
-- Stationary point found.
Frequency .log File
Low Frequency Analysis
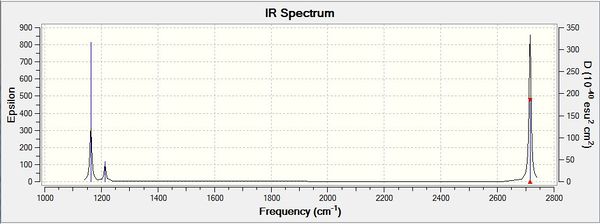
Low frequencies --- -2.2126 -1.0751 -0.0055 2.2359 10.2633 10.3194 Low frequencies --- 1162.9860 1213.1757 1213.1784
Frequency Table
| wavenumber (cm-1 | Intensity (arbitrary units) | symmetry | IR active? | type |
| 1163 | 93 | A2 | yes | out-of-plane bend |
| 1213 | 14 | E | yes | bend |
| 1213 | 14 | E | yes | bend |
| 2582 | 0 | A1 | no | symmetric stretch |
| 2700 | 126 | E | yes | asymmetric stretch |
| 2715 | 126 | E | yes | asymmetric stretch |
IR Spectrum
There are only 3 peaks produced from 6 different vibrations. This can be explained by the fact that two pairs of degenerate vibrations (the vibrations at 2715-1, and the vibrations at 1213 -1) which will each produce only one IR peak, as they abosrb at the same energy. Also the vibration at 2582cm-1 is symmetric and therefore IR inactive, it does not absorb IR radiation. This reduces the 6 vibrations to only 3 observed peaks
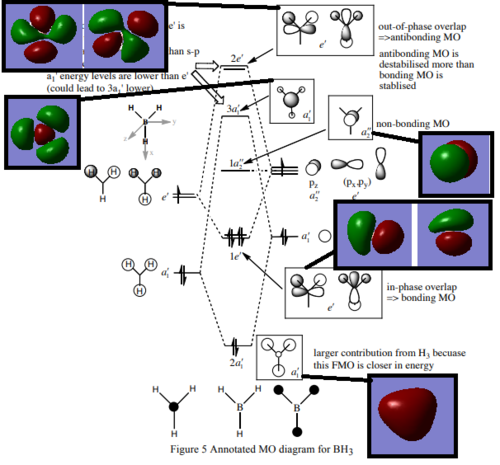
MO Diagram
Q: Are there any significant differences between the real and LCAO MOs? What does this say about the accuracy and usefulness of qualitative MO theory?
There are no major differences between the MO we calculated and the MO's produced from LCAO. This suggests that for the basic shape and structure of MO's, LCAO is an accurate and useful method. However LCAO assumes that only neighboring orbitals contribute to a MO. In reality all AO from the system contribute to form all the MO's, which explains the small differences between the LCAO and calculated MO's
Dynamic Image
BH3 |
NH3
Method & Basis Set
RB3LYP
6-31G(d,p)
Summary Table
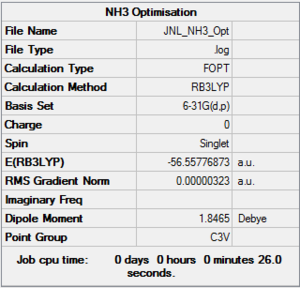
Item Table
Item Value Threshold Converged?
Maximum Force 0.000006 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000012 0.001800 YES
RMS Displacement 0.000008 0.001200 YES
Predicted change in Energy=-9.843916D-11
Optimization completed.
-- Stationary point found.
Frequency .log File
Low Frequency Analysis
Low frequencies --- -8.5646 -8.5588 -0.0044 0.0454 0.1784 26.4183 Low frequencies --- 1089.7603 1694.1865 1694.1865
Dynamic Image
NH3 |
NH3BH3
Method & Basis Set
RB3LYP
6-31G(d,p)
Summary Table
Item Table
Item Value Threshold Converged?
Maximum Force 0.000123 0.000450 YES
RMS Force 0.000058 0.000300 YES
Maximum Displacement 0.000515 0.001800 YES
RMS Displacement 0.000296 0.001200 YES
Predicted change in Energy=-1.635696D-07
Optimization completed.
-- Stationary point found.
Frequency .log File
Low Frequency Analysis
Low frequencies --- -0.0007 0.0004 0.0015 18.3844 27.7829 40.0656 Low frequencies --- 266.4161 632.3928 639.8576
Dynamic Image
NH3BH3 |
ΔE
E(NH3)= -26.615 a.u
E(BH3)= -56.558 a.u
E(NH3BH3)= -83.225 a.u
ΔE=E(NH3BH3)-[E(NH3)+E(BH3)] = -0.052 a.u ≈ 137 kJ/mol
Q: Based on your energy calculation is the B-N dative bond weak, medium or strong? What comparison have you made to come to this conclusion?
B-N Bond dissociation energy is 377.9 ± 8.7 kJmol-1 [1] Therefore the B-N dative bond is weak compared to a diatomic B-N bond.
Ng611 (talk) 13:47, 5 June 2018 (BST) Unfortunately, you've rounded to too few decimal places (3 dp instead of 5 dp, and this has caused your final value to be off by a few kJ/mol)
BBr3
Method & Basis Set
B3LYP
B: 6-31G(d,p)
Br: LANL2DZ
Summary Table
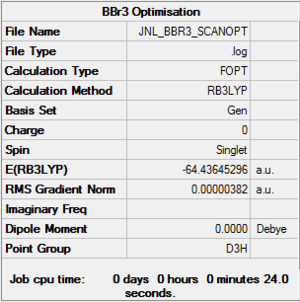
Item Table
Item Value Threshold Converged?
Maximum Force 0.000008 0.000450 YES
RMS Force 0.000005 0.000300 YES
Maximum Displacement 0.000036 0.001800 YES
RMS Displacement 0.000023 0.001200 YES
Predicted change in Energy=-4.026880D-10
Optimization completed.
-- Stationary point found.
Frequency .log File
Low Frequencies
Low frequencies --- -0.0137 -0.0064 -0.0046 2.4315 2.4315 4.8421 Low frequencies --- 155.9631 155.9651 267.7052
Dynamic Image
BBr3 |
Project
Benzene
Method & Basis Set
B3LYP 6-31G (d,p)
Summary Table
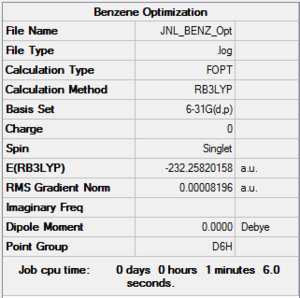
Item Table
Item Value Threshold Converged?
Maximum Force 0.000193 0.000450 YES
RMS Force 0.000079 0.000300 YES
Maximum Displacement 0.000830 0.001800 YES
RMS Displacement 0.000294 0.001200 YES
Predicted change in Energy=-4.437902D-07
Optimization completed.
-- Stationary point found.
Frequency .log File
Low Frequencies
Low frequencies --- -17.2053 -14.9372 -14.9372 -0.0054 -0.0054 0.0005 Low frequencies --- 414.1053 414.1053 620.9426
Dynamic Image
Benzene |
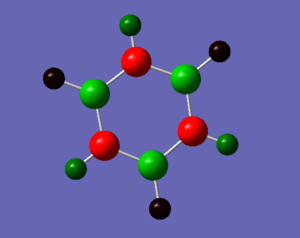
Borazine
Method & Basis Set
B3LYP 6-31G (d,p)
Summary Table
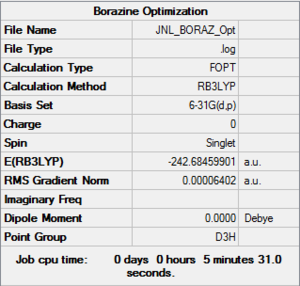
Item Table
Item Value Threshold Converged?
Maximum Force 0.000085 0.000450 YES
RMS Force 0.000033 0.000300 YES
Maximum Displacement 0.000250 0.001800 YES
RMS Displacement 0.000075 0.001200 YES
Predicted change in Energy=-9.266551D-08
Optimization completed.
-- Stationary point found.
Frequency .log File
Low Frequencies
Low frequencies --- 0.0004 0.0008 0.0012 3.4393 4.3291 6.8386 Low frequencies --- 289.7037 289.7792 404.4212
Dynamic Image
Borazine |
Charge Analysis
| Molecule | Comparison Charge Colour Diagram | Charge Values | Comment |
|---|---|---|---|
| Benzene |  |
C=-0.239 H=0.239 | Seeing as Carbon and Hydrogen have similar electronegativity values, 2.55 & 2.20 respectively, the bonds are not very polarized and mostly display covalent character. Therefore carbon will only carry a little more electron density than Hydrogen, as it is slightly more electronegative. This can be seen on the charge analysis where both Carbon and Hydrogen atoms are a dark shade of red or green, representing a small charge of -0.239 and 0.239 on each atom respectively. |
| Borazine |  |
N=-1.102 H=0.432 B=0.747 H=-0.077 | On the other hand in Borazine, the Nitrogen atoms are much more electronegative than the Hydrogen atoms, with a Pauling electronegativity of 3.04 compared to 2.20. Therefore the nitrogen Hydrogen bond is quite polarized resulting in an electron rich Nitrogen and an electron deficient Hydrogen. This can be seen in the Charge-Colour Diagram where the Nitrogen atoms are a bright shade of red, representing a charge of -1.102, and the Hydrogen's attached to them are a bright green colour (compared to the dark B-H hydrogens, or C-H hydrogens found in Benzene), representing a high positive charge of 0.432.
The Boron atoms are less electronegative compared to Hydrogen. This results in a reversal of charges that we previously saw in benzene C-H and Borazine N-H bonds. The Hydrogen is represented as black in the charge colour diagram, due to it's small negative charge of -0.077, and the Boron is represented as a light green colour due to it's 0.747 positive charge. |
Ng611 (talk) 13:50, 5 June 2018 (BST) Good discussion of the effects of electronegativity on the overall charge distribution. What do the partial charges sum to, and is there any difference in partial charge for atoms related by symmetry?
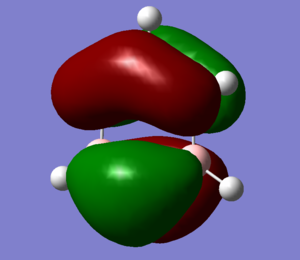
MO Analysis
| Energy Level | Benzene | Borazine | Comment |
|---|---|---|---|
| Benzene:21 Borazine:20 |  |
 |
The MO displayed here is the HOMO for Benzene, however it was found at one energy level below the HOMO in Borazine. It can be classified as a π-bonding MO since a rotation of 180 degrees about the internuclear axis will result in a change of sign. The overall character of the MO is bonding due to the in phase contributions below and above the nodal plane through the middle of the molecule, however this nodal plane is an anti-bonding contribution to the MO, and is quite significant as it is internuclear. The contributing atomic orbitals in both cases are pz orbitals of the same phase on the bottom half of the molecule, and pz orbitals of the opposite phase on the top half. Borazine has a slightly less symmetric system than benzene in this orbital, as can be seen from the larger contributions on each Boron atom. This is because this MO is quite high energy and will have a larger contribution from the more electropositive boron atom. |
| Benzene:17 Borazine:17 |  |
 |
This MO was found at Energy Level 17 for both Benzene and Borazine. It can be classified as a π-bonding MO since a rotation of 180 degrees about the internuclear axis will result in a change of sign. It is in fact the first and most symmetrical π-bonding MO, giving it a strong bonding character due to the all in phase AO interactions. The contributing AO's are the same phase pz orbitals on each atom in the hexagonal ring. For Benzene the electron distribution is much more symmetrical, however for Borazine the electron distribution is more hexagonal, due to the low energy electronegative nitrogen AO's giving a larger contribution to this low energy bonding MO. |
| Benzene:15 Borazine:13 |  |
 |
The final MO being compared was found at E15 for Benzene and E13 for Borazine. It can be classified as a σ-bonding MO seeing as a rotation about the internuclear axis does not result in a change of phase. In both benzene there is a bonding contribution between the px/y orbitals in the centre of the molecule, and a bonding interaction between the px/y orbital and the Hydrogen 1s orbitals. This occurs with opposite phase on the other side of the molecule resulting in a nodal plane down the centre of the system which is antibonding. The same basic structure can be seen in Borazine, however there seems to be an extra contribution on the bottom nitrogen atom, maybe from its lone pair in a px/y orbital. |
Aromaticity
The structure of Benzene, the archetypal aromatic molecule, was deduced from 3 main properties associated with it. Firstly Benzene had bond lengths which were all equal, as determined by X-Ray diffraction, and the bond length was somewhere between a double and single bond. Secondly the energy of hydrogenation was -152kJmol-1 less than would have been expected for a hexatriene, as determined by calorimetry. Finally the chemical shift for the hydrogen atoms outside of the Benzene ring were very high (7.27 ppm) compared to a typical alkene proton. Famously using this information, Kekule discovered the ring structure of alternating double and single bonds for Benzene.[3]
In this way aromaticity can be simply described as a cyclical series of pz on each atom of a system, each contributing some electron density to produce an overall delocalised cloud of electrons above and below the ring. Therefore 4 rules were empirically determined to define Aromaticity:
1) a conjugated delocalised π system (found in an alternating single-double bond pattern)
2) A flat structure
3) A Cyclical structure
4) There must be 4n + 2 π-electrons (Known as Hückel's rule) [4]
However, this description is insufficient to fully describe aromaticity. Firstly aromaticity has been observed in non-planar molecules, for example para-/meta- cyclophanes, and even 3D systems like polyhedral boranes. Additionally scientists have postulated that the σ-electron structure may have an important contribution to aromaticity, in addition to the π-electrons[5]. It can be seen from the MO's of benzene & Borazine that only 1 out of 21 corresponds directly to the overlapping pz atomic orbital description . In reality aromaticity is better understood through MO theory. For Benzene 6 pz atomic orbital combine to form 6 MO's, 3 of which are bonding orbitals and occupied. for Borazine and Benzene MO's 17, 20 & 21.
- ↑ http://staff.ustc.edu.cn/~luo971/2010-91-CRC-BDEs-Tables.pdf.
- ↑ https://en.wikipedia.org/wiki/Electronegativity
- ↑ https://www.imperial.ac.uk/media/imperial-college/research-centres-and-groups/spivey-group/teaching/org1aromatics/lecture11718.pdf
- ↑ https://en.wikipedia.org/wiki/Aromaticity
- ↑ Application of AIM Parameters at Ring Critical Points for Estimation ofp-Electron Delocalization in Six-Membered Aromatic andQuasi-Aromatic Rings, DOI: 10.1002/chem.200700250