Hw4717
NH3 molecule
General Molecular Information
| N-H bond distance | 1.01798 Angstrom radius |
| H-N-H bond angle | 105.741 degrees |
Optimisation Information
| molecule name | NH3 |
|---|---|
| calculation method | RB3LYP |
| basis set | 6-31G(d,p) |
| final energy E in (a.u.) | -56.55776873 |
| RMS gradient in (a.u.) | 0.00000485 |
| point group | C3V |
Item Table
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES
Jmol Dynamic Image
NH3 molecule |
The optimisation file is linked to here
Vibrations
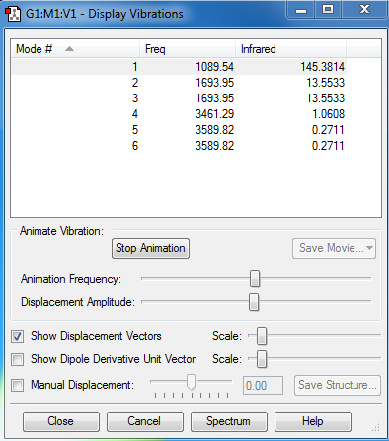
The rule to calculate vibration modes for a non-linear molecule is 3N-6, where the symbol N represents the number of atoms inside one molecule. As there are in total 4 atoms in one NH3 molecule, there should be (3*4 - 6 = ) 6 vibration modes to be expected.
From the graph, it can be seen that vibration modes #2 and #3 (with frequency at 1693.95 cm-1) are degenerate. Similarly, vibration modes #5 and #6 (with frequency at 3589.82 cm-1) are of degeneracy.
What is more, vibration modes #1, #2 and #3 are considered as "bending" vibrations. On the other hand, vibration modes #4, #5 and #6 are called "bond stretch" vibrations.
There are two modes which are highly symmetric. In the first one (with frequency at 1089.54 cm-1), all three bonds are bending inwards. In the fourth mode (with frequency at 3461.29 cm-1), all three bonds are stretching outwards. The rotating angles of symmetry are both 120 degrees.
The first vibration mode (with frequency at 1089.54 cm-1) is known as the "umbrella" mode.
In an experimental spectrum of gaseous ammonia, there are four bands would be expected, with frequency at 1089.54 cm-1, 1693.95 cm-1, 3461.29 cm-1 and 3589.82 cm-1.
Atomic Charges
Due to much higher electronegativity of nitrogen compared to the hydrogen, the electrons are theoretically pushed towards the nitrogen atom. This will result in a negative charge on the nitrogen atom and the positive charge on the hydrogen atom. Based on the computed data, the atomic charge of nitrogen is -1.125 and that of hydrogen is 0.375 in one ammonia molecule.
N2 molecule
General Molecular Information
| N-N bond distance | 1.10550 Angstrom radius |
| bond angle | linear (no bond angle) |
Optimisation Information
| molecule name | N2 |
|---|---|
| calculation method | RB3LYP |
| basis set | 6-31G(d,p) |
| final energy E in (a.u.) | -109.52412868 |
| RMS gradient in (a.u.) | 0.00000060 |
| point group | D*H |
Item Table
Item Value Threshold Converged? Maximum Force 0.000001 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES
Jmol Dynamic Image
N2 molecule |
The optimisation file is linked to here
Vibrations
| vibration mode number | frequency |
| 1 | 2457.33 cm-1 |
Atomic Charges
N2 is a non-polar molecule. Therefore, there is no charge on each of the nitrogen atom and there is no dipole moment.
H2 molecule
General Molecular Information
| N-N bond distance | 0.74279 Angstrom radius |
| bond angle | linear (no bond angle) |
Optimisation Information
| molecule name | H2 |
|---|---|
| calculation method | RB3LYP |
| basis set | 6-31G(d,p) |
| final energy E in (a.u.) | -1.17853936 |
| RMS gradient in (a.u.) | 0.00000017 |
| point group | D*H |
Item Table
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000001 0.001200 YES
Jmol Dynamic Image
H2 molecule |
The optimisation file is linked to here
Vibrations
| vibration mode number | frequency |
| 1 | 4465.68 cm-1 |
Atomic Charges
H2 is a non-polar molecule. Therefore, there is no charge on each of the hydrogen atom. In addition, there will be no dipole moment.
The Haber-Bosch process
Reaction Energies
| Energy required | Value in a.u. | Value in kJ/mol |
| E(NH3) | -56.55776873 | -148492.4218 |
| 2*E(NH3) | -113.1155375 | -296984.8436 |
| E(N2) | -109.52412868 | -287555.5998 |
| E(H2) | -1.17853936 | -3094.25509 |
| 3*E(H2) | -3.53561808 | -9282.765269 |
| ΔE=2*E(NH3)-[E(N2)+3*E(H2)] | -0.05579074 | -146.4785879 |
The gaseous reagents are more stable than the ammonia product due to lower energy. The positive value of the energy change during the reaction makes the product higher in energy. In addition, H-H bond and nitrogen triple bond are strong bonding, which is difficult to be broken.
CH4 molecule
General Molecular Information
| C-H bond distance | 1.09197 Angstrom radius |
| H-C-H bond angle | 109.471 |
Optimisation Information
| molecule name | H2 |
|---|---|
| calculation method | RB3LYP |
| basis set | 6-31G(d,p) |
| final energy E in (a.u.) | -40.52401404 |
| RMS gradient in (a.u.) | 0.00003263 |
| point group | TD |
Item Table
Item Value Threshold Converged? Maximum Force 0.000063 0.000450 YES RMS Force 0.000034 0.000300 YES Maximum Displacement 0.000179 0.001800 YES RMS Displacement 0.000095 0.001200 YES
Jmol Dynamic Image
CH4 molecule |
The optimisation file is linked to here
Vibrations
| vibration mode number | frequency |
| 1 | 1356.20 cm-1 |
| 2 | 1356.20 cm-1 |
| 3 | 1356.20 cm-1 |
| 4 | 1578.58 cm-1 |
| 5 | 1578.58 cm-1 |
| 6 | 3046.46 cm-1 |
| 7 | 3162.33 cm-1 |
| 8 | 3162.33 cm-1 |
| 9 | 3162.33 cm-1 |
The vibration modes from 1 to 5 are the "bending" modes and the vibration modes from 6 to 9 are considered as the "stretching" modes. The first three vibration modes are degenerate. The infrared value of 14.1008 indicates one band to be expected in the experimental spectrum. In addition, vibration mode #1 and #2 are symmetric. The vibration modes #4 and #5 are also degenerate; however, they are not symmetric. The last three vibration modes are of degeneracy as well, while the vibration mode #7 and #8 are highly similar. The vibration mode #6 is highly symmetric. Based on the infrared value of 25.3343, there will be another band expected in the experimental spectrum of methane.
Atomic Charges
CH4 is a polar molecule. Therefore, there should be slightly negative charge, which is -0.930 on the carbon atom due to higher electronegativity of carbon than hydrogen. Positive charge of 0.233 will be allocated on each of the hydrogen atom.
Molecular Orbital Theory
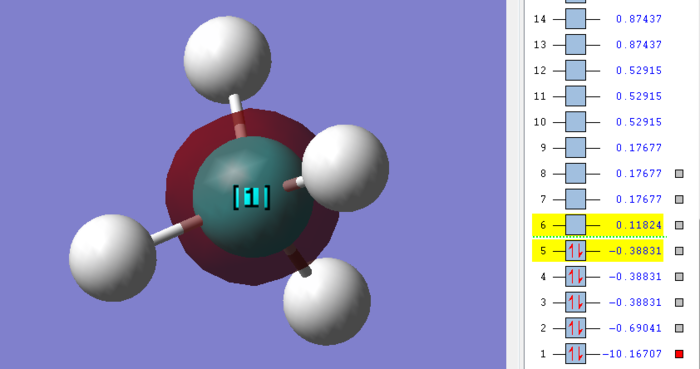
This is a graph of 1s atomic orbital of carbon atom, which contributes to the molecular bonding of methane. The orbital is a bonding orbital and is occupied. In order to form bonding between atoms in a molecule, the outer shell electrons are the elements taken into account. Therefore, this molecular orbital is deep in energy and will not be involved in the chemical reaction.
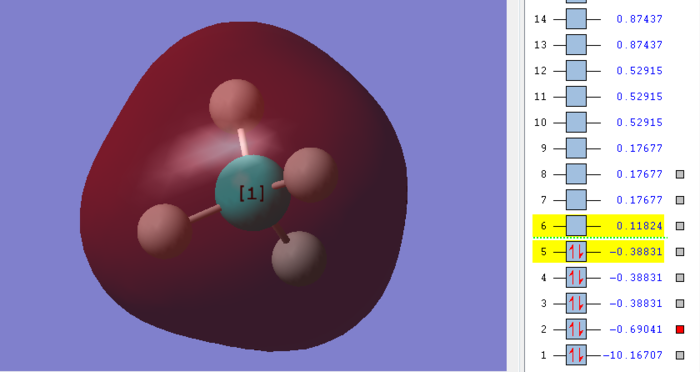
The diagram above shows the hybridization of 2s orbital and 1s orbital. The 2s atomic orbital is contributed from the carbon atom and the 1s atomic orbital is contributed from the hydrogen atom. This molecular orbital is a bonding orbital. What is more, this molecular orbital is deep in energy. Due to the assumption of sp3 hybridized orbital of methane, this molecular orbital is likely to be involved in the reaction. The two molecular orbitals of the lowest energy are fully occupied based on the Aufbau and Paulli exclusion principles. In the bonding molecular orbital, which is assigned due to the same sign on each side of the nodal plane, the density and probability of electrons between two nuclei increases. Furthermore, the energy becomes lower than its original level. it is easier to form bonding.
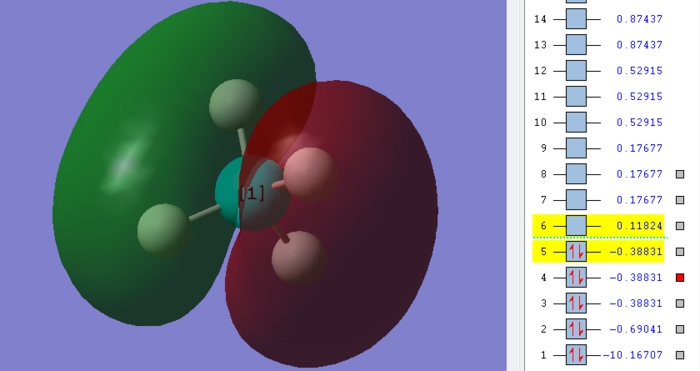

These two are 2p - 1s molecular orbital. The linear combination is contributed from the 2p valence orbital of carbon and the 1s valence orbital of hydrogen. This is a bonding molecular orbital and it is fully occupied. There are in total three orbitals which are highly similar, which are 2px, 2py and 2pz. The diagrams above are two of those three orbitals. They are all considered as HOMO (highest occupied molecular orbital).

This is the diagram of a 3s molecular orbital, which is contributed from the carbon atom. It is an anti-bonding orbital and is also called "LUMO" (lowest unoccupied molecular orbital). In this orbital, the density and probability of electrons between two nuclei are much smaller. Thus the energy will sharply increase and makes it vey difficult to form a bond.
