Hsh16 inorgcomp
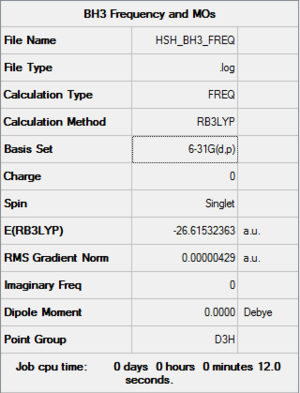
Day 1: BH3
- Computational method used: RB3LYP
- Basis set: 6-31G (d,p)
- Log file: Here!
- Jmol Representation:
Borane |
- Item table:
Item Value Threshold Converged?
Maximum Force 0.000009 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000034 0.001800 YES
RMS Displacement 0.000017 0.001200 YES
Predicted change in Energy=-4.343399D-10
Optimization completed.
-- Stationary point found.
- Low frequency table:
Low frequencies --- -2.2126 -1.0751 -0.0054 2.2359 10.2633 10.3194 Low frequencies --- 1162.9860 1213.1757 1213.1784
Additional Information
1. Include a table listing the vibrations,their intensity and symmetry in your wiki. Careful with the accuracy of your numbers, check the accuracy page! Indicate in your table if a vibration is IR active or not and describe what kind of vibration it is.
| Mode | Frequency (cm-1) | Infrared Intensity | What type of vibration is it? | Is it IR active? |
|---|---|---|---|---|
| 1 | 1163 | 93 | Out of plane bend. | Yes. |
| 2 | 1213 | 14 | Bend. | Yes. |
| 3 | 1213 | 14 | Bend. | Yes. |
| 4 | 2582 | 0 | Symmetric stretch. | No. |
| 5 | 2715 | 126 | Asymmetric stretch. | Yes. |
| 6 | 2715 | 126 | Asymmetric stretch. | Yes. |
2. Take a snap-shot of the spectrum and include it in your wiki.
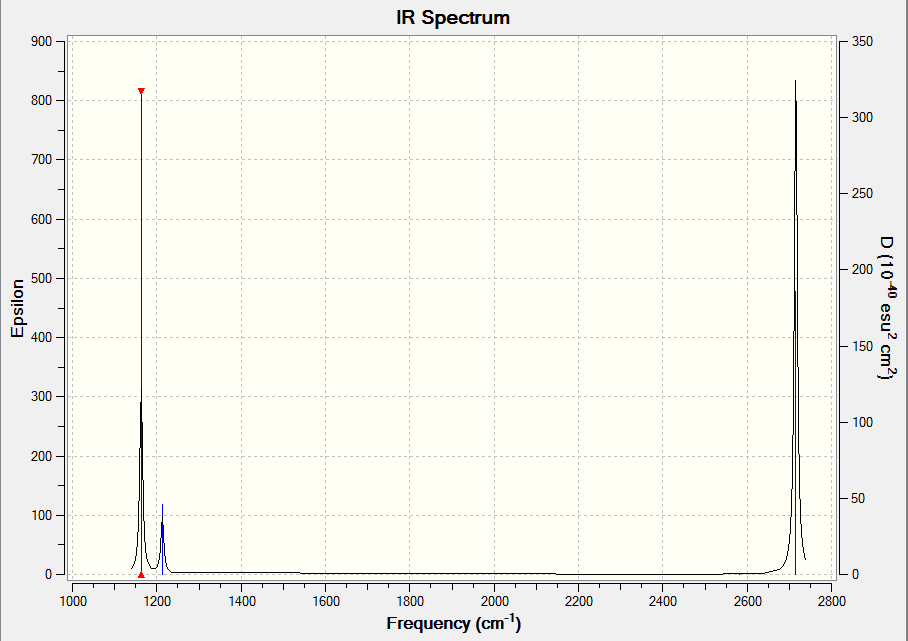
3. In your wiki explain why are there less than six peaks in the spectrum, when there are obviously six vibrations.
The IR spectrum shows only three peaks, which is less than the six vibrational modes described by Gaussian.
The fourth vibrational mode, with zero absorption intensity, is IR inactive as it does not lead to a change in the dipole moment of the molecule. Meanwhile, the remaining two missing peaks occur due to the degeneracy present in some of the other vibrational modes. The second vibrational mode, for instance, has the same frequency as the third vibrational mode. Additionally, the fifth vibrational mode has the same frequency as the sixth. Sharing of vibrational frequencies leads to degeneracy of the vibrational mode, which is manifested as absorptions on the same wavenumber as opposed to separate signals. This leads to a higher peak as absorptions at that frequency become stronger. As two of the modes are doubly degenerate, this accounts for the remaining two absorption peaks which are expected but missing on the IR spectrum leading to only three peaks being present on the IR spectrum.
Smf115 (talk) 16:34, 26 May 2018 (BST)Correctly assigned vibrational modes however, the symmetry assignments are missing. Nice explaination discussion both the degeneracy and the IR inactive peaks.
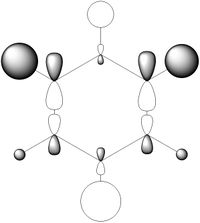
- MO diagram of BH3 with attached screenshots of computed orbitals.
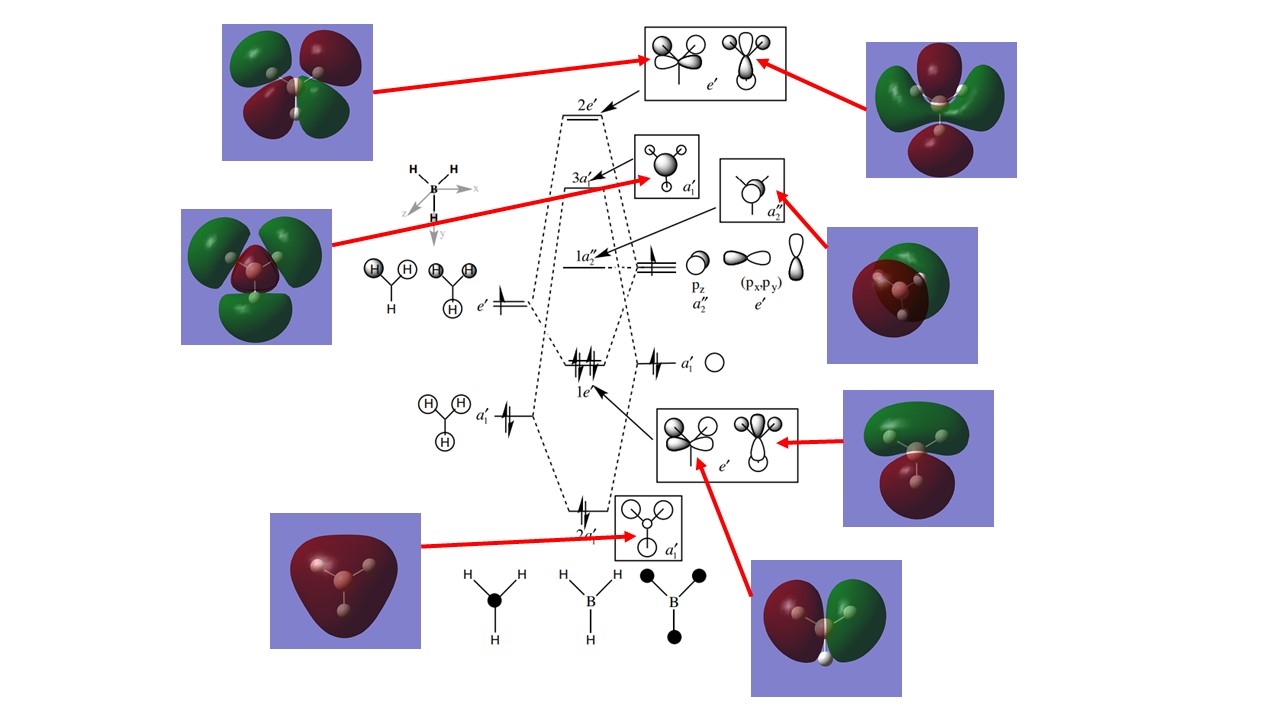
1. Are there any significant differences between the real and LCAO MOs?
Although the shapes of the computer and LCAO MOs are similar, the lobes of the real MOs are much larger than would be expected from the LCAO predictions. This can be seen in the 3a'1 MO, which has much larger lobes surrounding the hydrogen nuclei despite having a smaller contribution than boron under the LCAO version of the orbital. In addition to this, the LCAO models represent the fragment orbitals as separate entities as opposed to being combined as seen in the computed MOs. Additionally, the energetic ordering of the LCAO orbitals follows that of the computed model but it is not able to give exact values for the energies of the MOs.
2. What does this say about the accuracy and usefulness of qualitative MO theory?
From the differences above we can clearly say that qualitative MO theory is not the most accurate method available as it is unable to accurately represent real orbitals or give complete information on the physical quantities associated with a molecule. It is still, however, able to predict many properties of a given molecule such as its reactivity, charge distributions and structure and thus remains a useful tool for chemists especially when advanced computational methods are troublesome or unavailable.
Day 1: NH3
- Computational method used: RB3LYP
- Basis set: 6-31G (d,p)
- Log file: Here :)
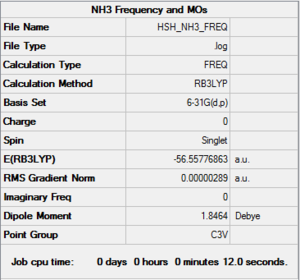
- Jmol Representation:
Ammonia |
- Item table:
Item Value Threshold Converged?
Maximum Force 0.000005 0.000450 YES
RMS Force 0.000003 0.000300 YES
Maximum Displacement 0.000012 0.001800 YES
RMS Displacement 0.000008 0.001200 YES
Predicted change in Energy=-9.075206D-11
Optimization completed.
-- Stationary point found.
- Low frequency table:
Low frequencies --- -11.5223 -11.4866 -0.0038 0.0245 0.1415 25.6160 Low frequencies --- 1089.6618 1694.1735 1694.1738
Day 1: NH3BH3
- Computational method used: RB3LYP
- Basis set: 6-31G (d,p)
- Log file: Here :)
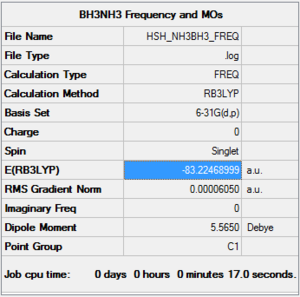
- Jmol Representation:
Borane-Ammonia Adduct |
- Item table:
Item Value Threshold Converged?
Maximum Force 0.000128 0.000450 YES
RMS Force 0.000057 0.000300 YES
Maximum Displacement 0.000769 0.001800 YES
RMS Displacement 0.000422 0.001200 YES
Predicted change in Energy=-1.750920D-07
Optimization completed.
-- Stationary point found.
- Low frequency table:
Low frequencies --- -0.0010 0.0010 0.0014 18.2560 22.7884 41.2425 Low frequencies --- 266.2735 632.3263 639.2585
Association Energy Questions
- E(NH3)= -26.62 Hartrees
- E(BH3)= -56.56 Hartrees
- E(NH3BH3)= -83.22 Hartrees
Association energy = E(Adduct) - E(BH3 + NH3)
= (-83.22) - (-56.56 + -26.62)
= -0.05 Hartrees
= 135 kJ mol-1
The B-N dative bond is weak relative to most covalent bonds. However it is still in the same order of magnitude of other bond energies of early periodic table elements (eg: C-C (348 kJ mol-1 or O-H (366 kJ mol-1)) so it is an acceptable value[1].
Day 1: BBr3
- Computational method used: GEN
- Basis sets: 6-31G (d,p) (B) and (LanL2DZ) (Br)
- Log file (via D-Space): DOI:10042/202420
- Jmol Representation:
Boron Tribromide |
- Item table:
Item Value Threshold Converged?
Maximum Force 0.000008 0.000450 YES
RMS Force 0.000005 0.000300 YES
Maximum Displacement 0.000036 0.001800 YES
RMS Displacement 0.000023 0.001200 YES
Predicted change in Energy=-4.026879D-10
Optimization completed.
-- Stationary point found.
- Low frequency table:
Low frequencies --- -0.0137 -0.0064 -0.0046 2.4315 2.4315 4.8421 Low frequencies --- 155.9631 155.9651 267.7052
Day 2: Aromaticity
Benzene
- Computational method used: B3LYP
- Basis set: 6-31G (d,p)
- Log file: Here :)
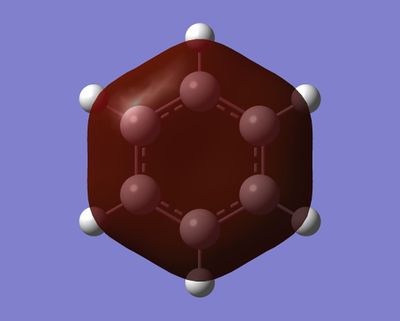
- Jmol Representation:
Benzene |
- Item table:
Item Value Threshold Converged?
Maximum Force 0.000197 0.000450 YES
RMS Force 0.000085 0.000300 YES
Maximum Displacement 0.000780 0.001800 YES
RMS Displacement 0.000333 0.001200 YES
Predicted change in Energy=-4.121162D-07
Optimization completed.
-- Stationary point found.
- Low frequency table:
Low frequencies --- -3.5606 -3.5606 -0.0088 -0.0042 -0.0042 10.0905 Low frequencies --- 413.9582 413.9582 621.1416
Borazine
- Computational method used: B3LYP
- Basis set: 6-31G (d,p)
- Log file: Here :)
- Jmol Representation:
Borazine |
- Item table:
Item Value Threshold Converged?
Maximum Force 0.000026 0.000450 YES
RMS Force 0.000010 0.000300 YES
Maximum Displacement 0.000097 0.001800 YES
RMS Displacement 0.000041 0.001200 YES
Predicted change in Energy=-5.708962D-09
Optimization completed.
-- Stationary point found.
- Low frequency table:
Low frequencies --- -9.0780 -8.7457 -8.4876 -0.0102 -0.0084 0.1180 Low frequencies --- 289.2035 289.2122 403.8165
An NBO Charge Comparison of Benzene & Borazine
| Benzene | Borazine | |
|---|---|---|
| Charge(s) on H | +0.239 (Bonded to C) | -0.077 (Bonded to B) +0.432 (Bonded to N) |
| Charge(s) on Ring Atoms | -0.239 (C) | -1.102 (N) +0.747 (B) |
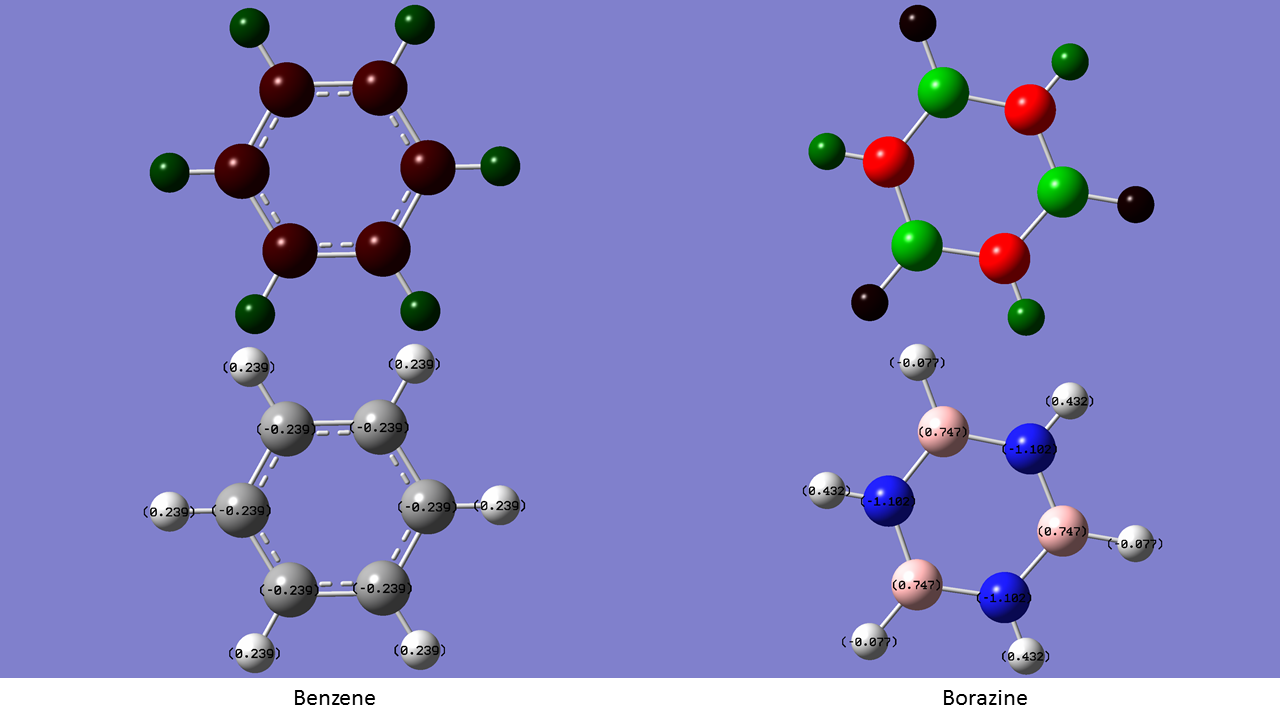
The charge distribution on benzene is very symmetric, with uniform charge distributions throughout the molecule. Neither carbon nor hydrogen are very highly polarised, with carbon having a NBO charge value of -0.239 and hydrogen having +0.239. This can be attributed to the similar Pauling electronegativities of the atoms (2.2 on H, 2.5 on B) leading to a relatively nonpolar bond. On borazine, boron and nitrogen can be found instead of carbon. Boron has a similar electronegativity value to hydrogen of 2.0. Nitrogen meanwhile is far more elctronegative at 3.0. As a result, the charge distribution on borazine is less symmetric than that of benzene. The boron atoms, being the most electropositive in the molecule take on a positive charge value of +0.747. Nitrogen, being the most electronegative, attracts the most electron density to itself and takes on the most negative value of -1.102. The charge on hydrogen in borazine differs based on the atom it is bonded to. When bonded to boron, it takes on a negative value as it is more elctronegative than boron, thus taking on the negative charge density in the B-H bonds. The converse is true when bonded to nitrogen, with hydrogen taking on the positive charge density instead[2].
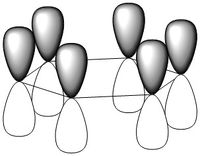
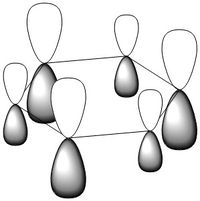
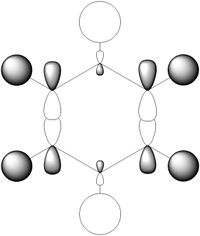
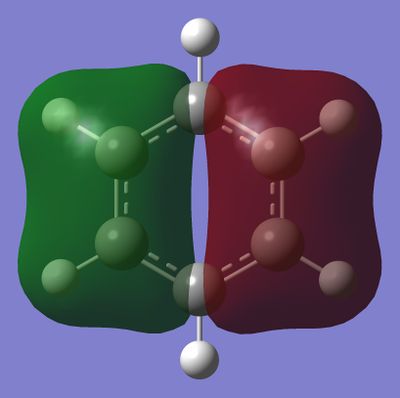
MO Comparison Between Benzene and Borazine
| MO Number | Benzene | Borazine | Similarities | Differences |
|---|---|---|---|---|
| 17 (π-type, bonding) |    |
   |
These are MOs that fit the "traditional"/qualitative depiction of the π orbital in an aromatic system with the strongest bonding character, having a contiguous pi-orbital system above and below the plane of the ring formed from the in-phase linear combination of pz orbitals of the ring atoms. As there are no contribution from the hydrogen atoms in the traditional model of aromaticity, there is no electron density surrounding the hydrogen nuclei in either molecule. | The shapes of the orbitals are slightly different for both molecules. The MO on benzene is shaped like a regular hexagon while the MO on borazine is a slightly irregular hexagon. This can be attributed to the nature of the atoms forming the aromatic ring. Benzene is made up of six identical carbon atoms which contribute equally from their isoenergetic 2p orbitals to this MO, leading to a regular shape and charge density around the ring. This is not the case with borazine which is comprised of electronegative nitrogen atoms and relatively electropositive boron atoms. This leads to differing contributions from the two species owing to the difference in energy of the atomic orbitals. As this MO is formed from a bonding combination, it receives greater contribution from the more electronegative nitrogen atoms which are lower and therefore closer in energy to the final orbital. |
| 18 (σ-type, some antibonding character) |   |
  |
These orbitals are high energy occupied σ orbitals with significant antibonding character present in both molecules. They are both higher in energy than the π orbitals of both molecules with the highest bonding character. This can be attributed to the strength of σ type interactions being greater than π type, allowing the combination of a σ interaction with significant antibonding character to rise in energy above a bonding π combination. Both orbitals have four nodes each, which is indicative of their antibonding character. These nodes, however, are through atoms, not through bonds so the destabilisation of the molecule is not severe. Additionally, there is some bonding character present in these MOs, as can be inferred from the interatomic regions with electron density. | The contributions on benzene are much more 'even' than those on borazine due to its higher symmetry resulting from the D6h point gorup. For instance, the benzene hydrogens on this MO either contribute a 'medium lobe' or a 'large lobe' to this MO. On borazine meanwhile, the fragment contributions are less symmetric. A 'very small lobe' is present on the hydrogen atom bonded to nitrogen in addition to the two mentioned for benzene. This is indicative of the differences in contribution from the two atom fragments which again results from the differences in energy between the boron and nitrogen atoms. |
| 8 (σ-type, bonding) |   |
  |
These are both bonding orbitals derived from symmetry adapted linear combinations of 2s atomic orbitals in a ring merging in phase with their same-symmetry counterparts of the 1s orbitals of the hydrogens grouped together in the same symmetry adapted linear combination. They are also not the orbitals with the highest bonding character becuase they are not totally symmetric. This can be attributed to the single nodal plane present in both MOs. | Owing to the symmetry of the molecules, these two orbitals are derived from combinations under two different symmetry adapted fragments. The orbital on benzene (which falls under the D6h point group) is derived from the doubly degenerate bonding combination of an L6 fragment whereas the orbital on borazine is derived from the doubly degenerate antibonding combination of the L3 fragment (which falls under the D3h point group). |
Smf115 (talk) 23:05, 26 May 2018 (BST)Excellent MO comparison, good range of MOs selected and the similarities and differences are clearly presented with the use of accurate terminology.
Aromaticity Discussion
The most basic definition of aromaticity originates from benzene. From there it was defined that aromatic molecules were planar, cyclic hydrocarbon molecules with a contiguous conjugated series of p-orbitals above and below the plane of the ring, with an occupancy of 4n + 2 electrons in the conjugated system (under Huckel's rule). This leads to the unexpected stability of the molecule due to a new set of delocalised orbitals being formed from the linear combination of the 2p orbitals around the ring. In addition to the stability, various other properties would result, including the formation of a ring current when exposed to an external magnetic field and the intermediate length of the carbon-carbon bonds in the ring between that of a double and a single bond. This definition was then generalised to accommodate molecules which displayed similar properties, like borazine or the P42- anion. In our investigation of benzene and borazine, this description fits the real orbitals quite well, with the frontier orbitals formed from the 2pz orbitals in the ring resembling the shape expected from the linear combinations of the orbitals involved.
However, this description of aromaticity has been disputed, as discussed in previous work by Palusiak and Krygowski[3]. For instance, it has been proven that aromatic molecules do not necessarily have to be planar and that even (initially) planar aromatic molecules can have their planarity disrupted while retaining their delocalised bonds. This would go against the traditional description of aromaticity which requires the planarity in order to allow for the interactions of the orbitals in the plane of the ring. Furthermore, hypotheses about the origin of aromaticity have been proposed that conflict with the traditional definition given above. This relates primarily to the contribution of the σ to the overall aromaticity of the molecule. This has not been concluded and remains a possibility to be looked into. Additionally, aromaticity has been shown to result from orbitals dz2 orbitals as well which do not fall under the traditional definition of aromaticity[4]. Owing to the numerous examples of aromaticity which do not fall under the basic definition, the concept of overlapping pz orbitals is therefore too rigid a criterion for defining aromaticity and should be reexamined.
Smf115 (talk) 00:24, 27 May 2018 (BST)Good discussion of aromaticty from the basic concepts and covering a range of ideas. To improve, consider the MOs just viewed and how these might illustrate how overlapping pZ AOs is a bad descriptor of aromaticity.
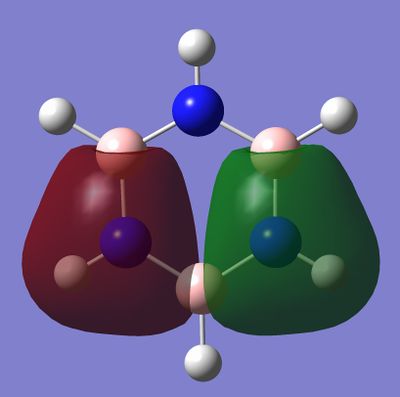
Stuff I Found Interesting lol
Most of the orbitals in benzene and borazine were similarly shaped with only minor differences in lobe distribution, however there were some orbitals which were very different (see thumbnails in this section). These were occupied at the ground state of both molecules, which would lead to differences in electron distribution, more so in borazine. This asymmetric orbital shape is perhaps the reason as to why borazine is considered a polar molecule.
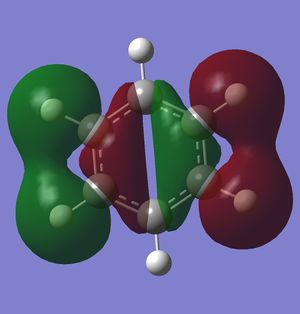
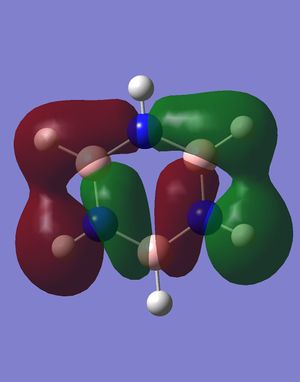
Smf115 (talk) 00:26, 27 May 2018 (BST)Nice to see something interesting highlighted and overall a very good wiki report.
References
- ↑ http://www.science.uwaterloo.ca/~cchieh/cact/c120/bondel.html
- ↑ Clayden, J., Greeves, N., & Warren, S. G. (2012). Organic chemistry. Oxford: Oxford University Press.
- ↑ Palusiak M, Krygowski TM. Application of AIM parameters at ring critical points for estimation of pi-electron delocalization in six-membered aromatic and quasi-aromatic rings. Chemistry. 2007;13(28):7996-8006.
- ↑ J. Am. Chem. Soc. 127, 15, 5701-5705