Hhc16Y2

Molecular Reaction Dynamics

Introduction

Triatomic reactions have the general form:

$\text{<mrow data-mjx-texclass="ORD">A<mo stretchy="false">+</mo>BC</mrow>}\to \text{<mrow data-mjx-texclass="ORD">AB<mo stretchy="false">+</mo>C</mrow>}$

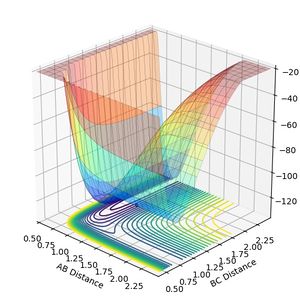
Molecular dynamics in triatomic reactions can be approximated in terms of a potential surface $V(x,y)$ generated (partly) by superimposing two orthogonal potential energy curves ('Leonard-Jones'-like potentials) complemented with quantum mechanical calculations, with one axis representing the incoming diatomic bond and the other representing the resulting diatomic bond. The potential energy surface contains three stationary points;

• the reactants at the beginning of the reaction;
• the products after the reaction and;
• the transition state.

The two former structures exist as local minima, where the the potential gradients along the initial bond and formed bond are both zero. The latter exist as a saddle point, where the gradients of the two components are equal and opposite thus cancelling out the overall gradient to zero. Once the potentials are known and stationary points found (by computing $\mathrm{\nabla }V(x,y)=0$), the two types of structures can be distinguished using the second partial differential test:

• If structure is a minima, then the Hessian of the potential function:$V_{xx}(x,y)V_{yy}(x,y)-{(V_{xy}(x,y))}^2>0$ and $V_{xx}(x,y)>0$
• If structure is a saddle, then the Hessian of the potential function: $V_{xx}(x,y)V_{yy}(x,y)-{(V_{xy}(x,y))}^2<0$

Where the Hessian is the determinant of the Hessian matrix applied to the potential function[1]. The reaction will proceed as described if the species collide with an energy greater than the local potential barrier at the transition saddle point.

(Very nice to see a concise introduction! Fjs113 (talk) 21:52, 17 May 2018 (BST))

H-H-H System

Consider a three hydrogen triatomic reaction:

${\mathrm{H}}_{\mathrm{2}}\mathrm{+}\mathrm{H}\to \mathrm{H}\mathrm{+}{\mathrm{H}}_{\mathrm{2}}$

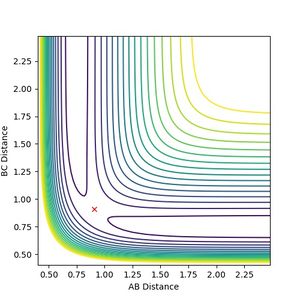
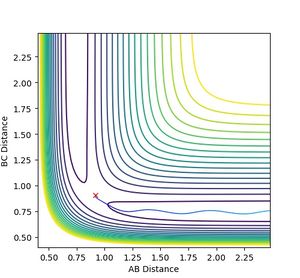
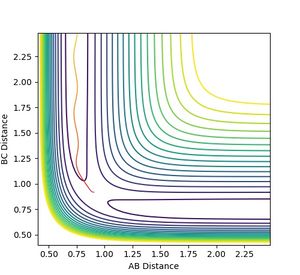
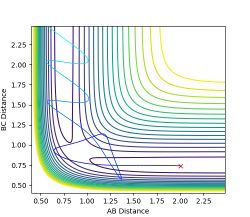
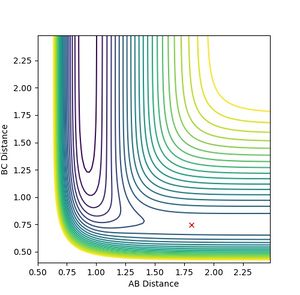
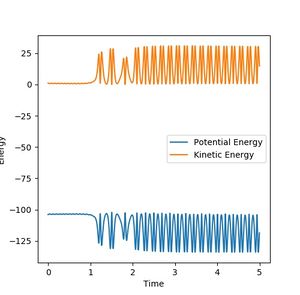
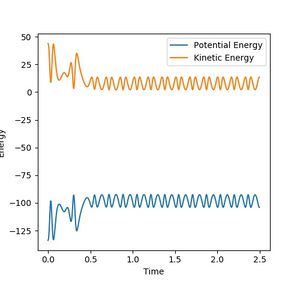
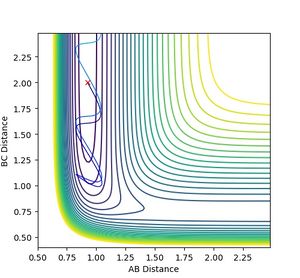
As the three atoms are identical, the potential surface is symmetrical. Hence the transition state is expected to occur when the three atoms are equidistant to each other. Using the simulator lepsgui.py, the transition state was found by setting the particle momenta to 0 and locating a bond distance on the saddle structure where the particle remains stationary on the potential surface. It is as though the molecule has potential to collapse into either reactant or product, yet does not have the inertia to do so. This distance was found to be 0.9075 A. The distance between the two end nuclei was found to be 1.815 A, consistent with double of the previous observation. Neither kinetic nor potential energy showed any change over time, consistent with theoretical behaviour at a stationary transition state.

• 
  Figure 1: Transition state on the saddle point of the hydrogen triatomic reaction potential.
• 
  Figure 2: Internuclear distances at the transition state.
• 
  Figure 3: Energy of the system.

Reaction Paths

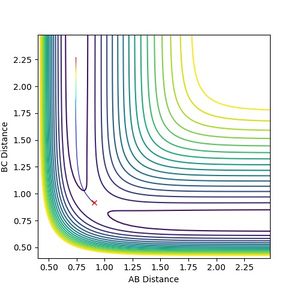
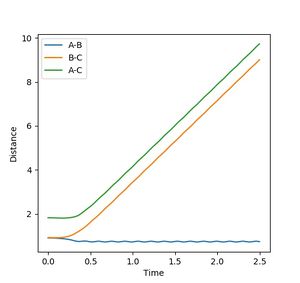
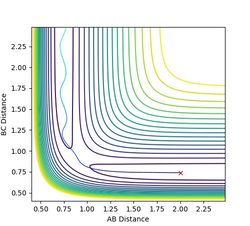
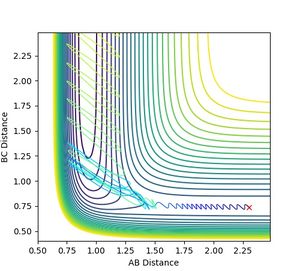
From the transition state it was also possible to find the minimum energy path (MEP) for the transition state to collapse into the product. This was achieved by starting the simulation with the particle displaced at a small distance (0.01 A) from the transition state and having no momentum. The particle effectively 'rolled off' the saddle point and travelled along the bottom of the potential valley, mapping out the path of minimum energy. It is useful for extracting information about the reaction: if the one dimensional path was mapped relative to only the height, a reaction profile plot can be obtained. Equilibrium geometries can also be found this way.

• 
  Figure 4a: Minimum energy path.
• 
  Figure 4b: Internuclear distance when reaction proceeds via minimum energy path.

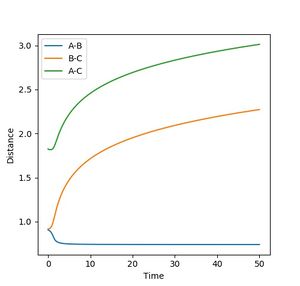
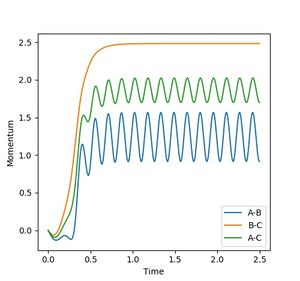
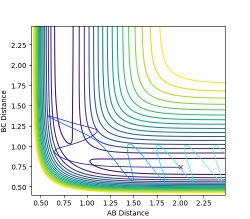
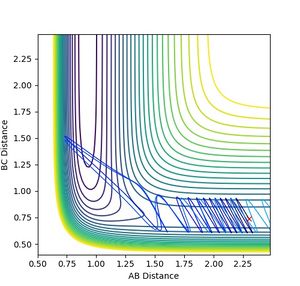
The MEP assumes an infinitely slow reaction where the velocity self adjusts. A more realistic representation would be one where the bond in the product oscillates. The path generated still follows that of the potential valley, but oscillates within the well. In this model the reaction collapses into the product much quicker as evident in the internuclear distance plot, where the dynamic system diverges further in shorter time.

• 
  Figure 5a: Dynamic reaction path. Notice the oscillation in the bond.
• 
  Figure 5b: Internuclear distance when reaction proceeds via the dynamic energy path. Components move away much faster than previous example.
• 
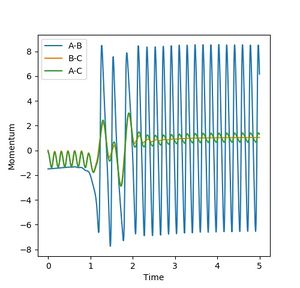
  Figure 5c: Internuclear momenta shows that the product is oscillating.

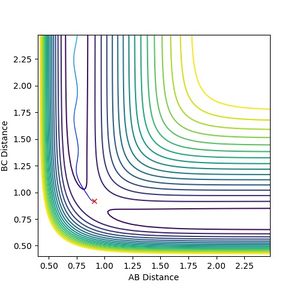
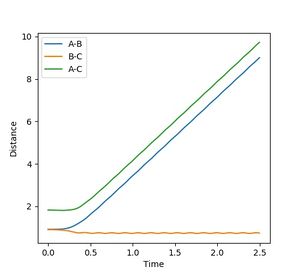
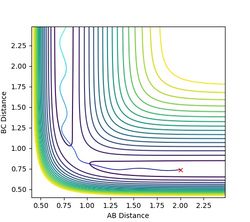
As the potential surface is symmetrical, regardless of which bond has an added small displacement the result will be the same but the reaction will proceed backwards.

• 
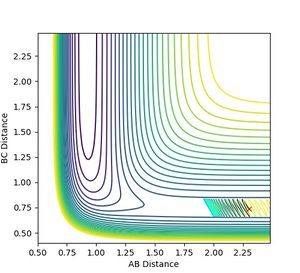
  Figure 6a: A reaction trajectory going the other way.
• 
  Figure 6b: The internuclear distance is the same but with labels swapped.

The final momenta and positions from the dynamic simulation were fed back into the simulator with reversed momentum. The resulting reaction path is the same but in the opposite direction, where the products return to the transition state and stays there.

• 
  Figure 7: Reverse reaction trajectory with system returning to transition state.

(Very good! Fjs113 (talk) 21:52, 17 May 2018 (BST))

Path Energy Considerations and Reactivity

Not all paths will lead to the crossing of the energy barrier via the transition state and result in a reaction. By fixing reactant H₂ bond at 0.72 A and distance between H and H₂ at 2.0 A, a range of momenta were tested to investigate whether or not they are reactive.

p1	p2	ETotal	Reactive	Path	Comments
-1.25	-2.5	-99.018	Yes		Trajectory passes over transition state.
-1.5	-2.0	-100.456	No		Trajectory bounces off the energy barrier and returns to the well.
-1.5	-2.5	-98.956	Yes		Trajectory passes over transition state with larger initial oscillation than case one.
-2.5	-5.0	-83.956	No		Although the trajectory passes over the energy barrier, the high momenta hence energy made the particle pass it again and return to the reactant state.
-2.5	-5.2	-83.416	Yes		Trajectory passes the barrier multiple times before collapsing into product.

Transition State Theory

The Transition State Theory[2] assumes that:

1. Particles behave classically.
2. Reactions proceed via the lowest energy saddle point
3. Once a system reaches the transition state, it collapses to products and reaction goes to completion.

In essence, all molecules must have enough energy to overcome the saddle point in order to generate product, hence the rate of product generation must be determined in some way by how high the energy barrier is.

This however breaks down when reactions occur via a much higher energy barrier instead of the transition state, or proceeds in some obscure way like crossing back to the reactant state (as the last case above). The rate of reaction will therefore be lower than predicted by the theory. It also fails to account for quantum mechanical effects such as tunneling, which will allow the particle to bypass the energy barrier without having the energy required to overcome it. Given tunneling only occurs with small masses and low energy barriers, the transition state theory will in most cases overestimate the rate of reaction.

(Barrier recrossing is definitely not "some obscure way". ;) Otherwise very good! Fjs113 (talk) 21:52, 17 May 2018 (BST))

F-H-H System

Consider a triatomic reaction between a fluorine atom and hydrogen:

$\mathrm{F}\mathrm{+}{\mathrm{H}}_{\mathrm{2}}\to \mathrm{H}\mathrm{F}\mathrm{+}\mathrm{H}$

The forward reaction (generation of HF) is exothermic, and the backward reaction (generation of hydrogen from hydrogen fluoride) is endothermic. The thermodynamics is evidenced by the potential surface for this reaction: the potential well for the H-F bond is deeper than that for H₂, in agreement with the former having a stronger bond than the latter. Using the same method for the triatomic hydrogen, the transition state bond distance was found to be 1.8112 A for H-F and 0.7452 A for H-H.

(Simply stating the TS initial conditions is not quite enough. You need to show your working, even if it's just an educated guess! Fjs113 (talk) 21:52, 17 May 2018 (BST))

• 
  Figure 8a: Potential surface for this system. Notice the deeper valley for the hydrogen fluoride product.
• 
  Figure 8b: Transition state for this system.

Activation Energy

The activation energy was determined by subtracting the reactant energies with the transition state energy. For the forward hydrogen fluoride generation reaction the activation was 0.23 kcal/mol, and the backward hydrogen generation reaction was 30.25 kcal/mol. There is some discrepancy between that reported in literature[3], possibly due to quantum effects lowering the energy requirement.

(Where did these values come from? What did you use to determing the different energy levels? Again, you need to show your working. Bare values don't show understanding. Fjs113 (talk) 21:52, 17 May 2018 (BST))

Reaction Dynamics

Forward Reaction

The forward reaction involves crossing a low transition barrier relative to the reactants (an early transition state). One of the various reaction trajectories leading to a successful forward reaction is H-H = 0.74 A, F - H2 = 2.3 A, fluorine hydrogen momentum -1.5, hydrogen bond momentum -0.1. As illustrated, the reaction almost returns to the reactants but crosses the potential barrier back to the products. Given the total energy of the system must stay the same by virtue of energy conservation, when the reactants collapse to the product, the drop in potential must be converted into both vibrational kinetic energy observed in the higher frequency oscillation of the product bond, and translational kinetic energy as the product moves away, as seen below. If the resulting oscillation is too rigorous or movement too rapid, it can cross the potential barrier again and return to the reactant. The nature of the kinetic energy evolution being a reflection of the potential energy evolution evidenced the interchange hence conservation of energy. Eventually the reaction proceeded into higher energy oscillations in the product. This can be verified experimentally using calorimetry - the higher kinetic energy will manifest itself as heat in the system, thus should be detectable as a temperature increase and in line with the exothermic nature of the forward reaction.

• 
  Figure 9a: Forward reaction trajectory.
• 
  Figure 9b: Energy evolution of the forward reaction. As the system collapses into the product notice the increase in kinetic energy and decrease in potential energy. Fluctuations are due to bond vibrations, with oscillations interchanging with potential stored in bond stretching/compression.
• 
  Figure 9c: Internuclear momenta evolution. The drop in potential after crossing the energy barrier makes the oscillation of the H-F bond large.

For hydrogen bond momenta around 3 or -3, with hydrogen fluorine momentum -0.5, H-H = 0.74 A and F - H2 = 2.3 A, the system pertained high vibrational but low translational energy. Despite total energy exceeding that of the activation energy, the reaction crossed the potential barrier but returned to products. It would appear that high vibrational energy does not favour the forward reaction as much as high translational energy.

• 
  Figure 10: Reaction does not proceed with p(F - H2) = -0.5, p(H-H) = 3.

However when the bond momentum is reduced, there are certain values that allowed the reaction to still proceed. For instance at bond momentum 2.29, the reaction was able to go to completion. This is in agreement with Polyani's Rules, which states that crossing of a late transition state is favoured by high vibrational energy modes than translational modes, whereas higher translational modes favour the crossing of early transition states. Below 1.48 reaction does not have enough energy to reach the transition state.

• 
  Figure 11: Reaction proceeds for p(F - H2) = -0.5 and p(H-H) = 3.
• 
  Figure 12: At or below 1.48 reaction does not pass transition state.

When the positions were kept the same but fluorine hydrogen momentum at -0.8 and hydrogen bond momentum at 0.1 the system goes through again. This is consistent with recent theoretical revisiting of the Rules which said that the Rules apply except when collision energies are low[4].

• 
  Figure 13: Low collision energy allows reaction to proceed as well.

Backward Reaction

The backward reaction involves crossing a high transition barrier relative to the reactants (a late transition state). One of the various reaction trajectories leading to a successful backward reaction is FH - H = 2.0 A, F-H = 0.925 A, hydrogen fluoride bond momentum -12.0, hydrogen fluorine momentum -4.0, obtained by setting low H-F bond momentum and high incident hydrogen momentum then tuning the two until a reaction occurs.

• 
  Figure 14a: Successful reaction.
• 
  Figure 14b: Kinetic energy drops and potential energy increases.

Note that the high vibrational energy of the H-F bond aids the crossing of the transition state more so than high translational energy. This again appears consistent with Polanyi's Rules.

• 
  Figure 15: Reaction does not proceed at p(H-F) = -0.05, p(H - HF) = -4.

(It seems that you never actually stated Polanyi's rules. But good that you provided results supporting them. Fjs113 (talk) 21:52, 17 May 2018 (BST))

(Would've been better if you had provided a list of references at the end. Fjs113 (talk) 21:52, 17 May 2018 (BST))