Molecular Orbital Calculations using Gaussian

In this laboratory molecular properties were derived from quantum mechanical calculations computed using the program Gaussian. Unless otherwise specified, the following calculations were performed using:

Method: B3LYP, where the Hamiltonian is obtained from a combination of different approximations and density functional theory, with calculations placing particular emphasis on the exchange integral.
Basis sets derived by Pople:
- 3-21G, where a linear combination of three time-averaged Gaussian density functions are used to model each core electron orbital.
- 6-31G(d,p), where six time-averaged Gaussian density functions are used instead of only three, with polynomial coefficients that allow for the presence of nodes and thus population of p and d orbitals.

Smf115 (talk) 12:10, 25 May 2018 (BST)Very nice additional detail showing awareness of the methods used (just missing the pseudopotential!)

Borane

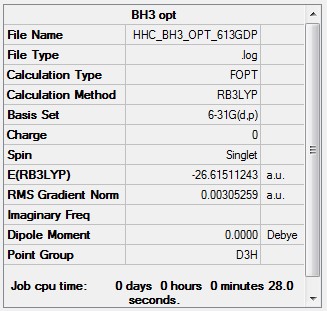
Optimised borane

Formula: BH₃
Method: B3LYP
Basis: 6-31G(d,p)
Optimisation:

         Item               Value     Threshold  Converged?
 Maximum Force            0.000004     0.000450     YES
 RMS     Force            0.000003     0.000300     YES
 Maximum Displacement     0.000017     0.001800     YES
 RMS     Displacement     0.000011     0.001200     YES
 Predicted change in Energy=-1.021830D-10
 Optimization completed.

Smf115 (talk) 12:09, 25 May 2018 (BST)Great structure information and the correct point group for the molecule. However, I think you've used the summary from the first step of your optimisation as the energy value is incorrect and different from the one of the optimised structure within the log file.

Frequencies:

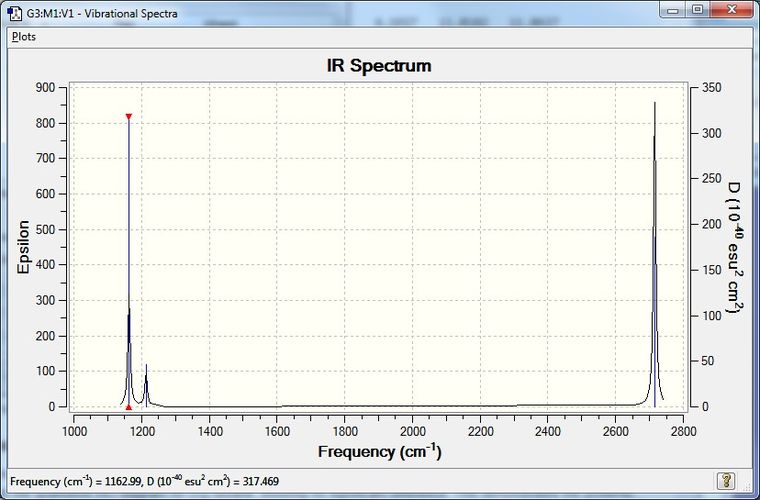
Low frequencies ---   -1.1800   -1.0028   -0.0055    4.1927   11.0182   11.0637
Low frequencies --- 1162.9912 1213.1792 1213.1819

Infrared Spectroscopy

The following are the vibrational modes for borane:

Vibrational Mode	Frequency /cm^-1	Intensity	IR Active	Type
1	1163	93	Yes	out-of-plane bend
2	1213	14	Weakly	bend
3	1213	14	Weakly	bend
4	2582	0	No	symmetric stretch
5	2715	126	Yes	asymmetric stretch
6	2715	126	Yes	asymmetric stretch

Note that mode 4 is not IR active, as the oscillation does not generate a transition dipole moment. Note also that modes 2-3 and 5-6 form degenerate pairs, thus have the same IR absorption frequency. The expected spectrum thus contains only three peaks, with spectral features for the degenerate modes superimposing.

Figure 1: Predicted IR spectrum of borane.

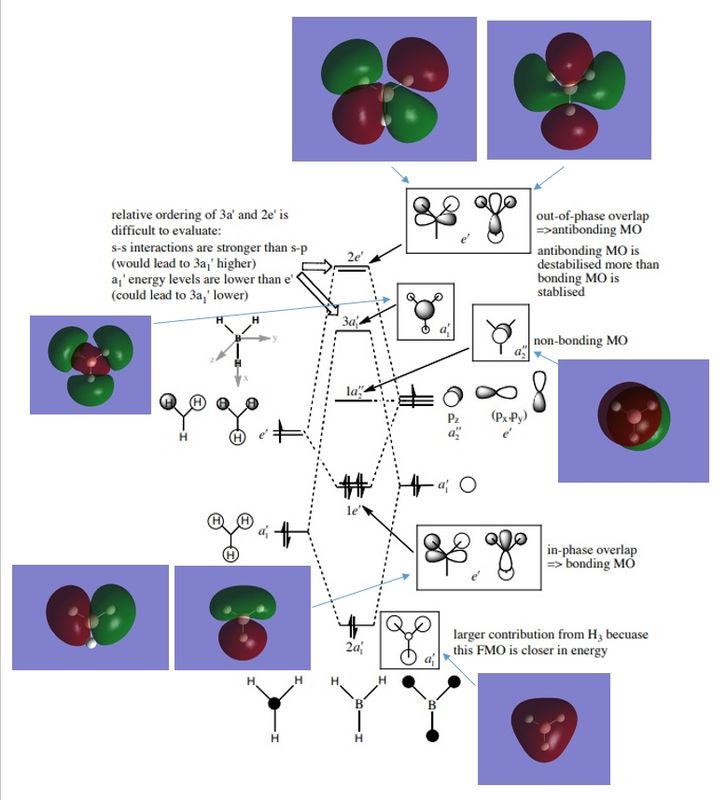
Molecular Orbital

The molecular orbitals for borane were generated. As illustrated, the calculated molecular orbitals seem to agree with the qualitative MO diagram for D_3h borane[1] when lobes are combined according to phase. There are however some discrepancies: for example the Gaussian computed 3a₁ orbital has large hydrogen lobes, where MO theory predicts a low hydrogen contribution. This demonstrates that qualitative molecular orbital diagrams have relatively good predictive power for behaviour of simple molecules when computation is unavailable, however it does not provide relative energies (incredibly useful for predicting reaction thermodynamics) and may break down at times.

Figure 2. Qualitative MO diagram compared with Gaussian computed MO's.

Ammonia

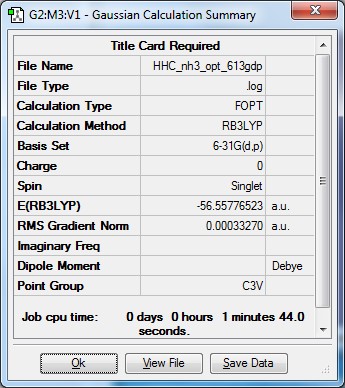
Optimised ammonia

Formula: NH₃
Method: B3LYP
Basis: 6-31G(d,p)
Optimisation:

         Item               Value     Threshold  Converged?
 Maximum Force            0.000005     0.000450     YES
 RMS     Force            0.000003     0.000300     YES
 Maximum Displacement     0.000010     0.001800     YES
 RMS     Displacement     0.000007     0.001200     YES
 Predicted change in Energy=-7.830785D-11
 Optimization completed.

Frequencies:

Low frequencies ---   -0.0253   -0.0069   -0.0030   41.5002   61.8483   61.8549
 Low frequencies --- 1102.3714 1695.4596 1695.4600

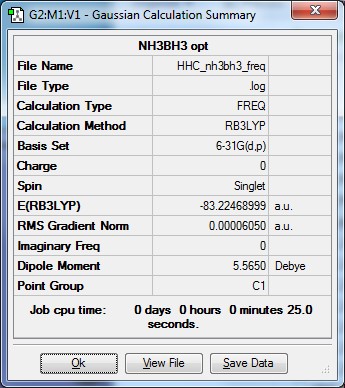
Ammonia Borane

Optimised ammonia borane

Formula: NH₃BH₃
Method: B3LYP
Basis: 6-21G(d,p)
Optimisation:

         Item               Value     Threshold  Converged?
 Maximum Force            0.000139     0.000450     YES
 RMS     Force            0.000063     0.000300     YES
 Maximum Displacement     0.000771     0.001800     YES
 RMS     Displacement     0.000338     0.001200     YES
 Predicted change in Energy=-2.028054D-07
 Optimization completed.

Frequencies:

Low frequencies ---   -0.0014   -0.0014   -0.0006   18.2561   22.7884   41.2426
 Low frequencies ---  266.2735  632.3263  639.2586

Energy of Formation

The energy of formation for this molecule, in this case the association energy of the can be determined from energies calculated above.

E(NH₃) = -56.56 hartree
E(BH₃) = -26.62 hartree
E(NH₃BH₃) = -83.22 hartree
ΔE = E(NH₃BH₃)-[E(NH₃)+E(BH₃)] = -0.05 hartree = 131 kJmol^-1

Compared with a C-C bond (on the order of 300 kJmol^-1), the B-N bond is mildly stable. This likely explains its relative chemical stability, making it a prime candidate for hydrogen storage in automobiles [2]

Smf115 (talk) 12:06, 25 May 2018 (BST)Very nice reference to a relevant application for the molecule and correct calculation procedure. To improve make sure the literature value for the C-C bond is referenced too and consider the accruacy of the numbers used within calculations.

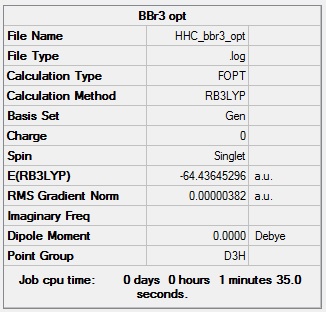
Boron Tribromide

Optimised boron tribromide

Formula: BBr₃
Method: B3LYP
Basis: GEN (General basis set: 6-31G(d,p) for B and LanL2DZ for Br)
Optimisation:

         Item               Value     Threshold  Converged?
 Maximum Force            0.000008     0.000450     YES
 RMS     Force            0.000005     0.000300     YES
 Maximum Displacement     0.000036     0.001800     YES
 RMS     Displacement     0.000023     0.001200     YES
 Predicted change in Energy=-4.027377D-10
 Optimization completed.

Frequencies:

Low frequencies ---   -0.0137   -0.0064   -0.0046    2.4315    2.4315    4.8421
 Low frequencies ---  155.9631  155.9651  267.7052

DSpace: DOI:10042/202421

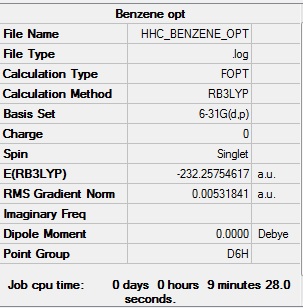
Benzene

Optimised benzene

Formula: C₆H₆
Method: B3LYP
Basis: 6-31G(d,p)
Optimisation:

Item               Value     Threshold  Converged?
 Maximum Force            0.000199     0.000450     YES
 RMS     Force            0.000081     0.000300     YES
 Maximum Displacement     0.000847     0.001800     YES
 RMS     Displacement     0.000299     0.001200     YES
 Predicted change in Energy=-4.636467D-07
 Optimization completed.

Frequencies:

 Low frequencies ---   -4.6046   -4.6046   -0.0088   -0.0042   -0.0042    9.6590
 Low frequencies ---  413.9386  413.9386  621.1428

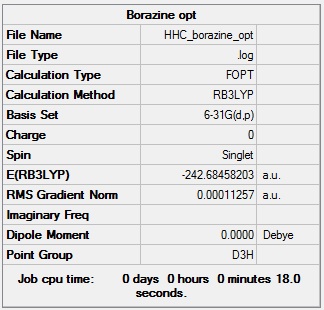
Borazine

Optimised borazine

Formula: N₃B₃H₆
Method: B3LYP
Basis: 6-31G(d,p)
Optimisation:

        Item               Value     Threshold  Converged?
 Maximum Force            0.000187     0.000450     YES
 RMS     Force            0.000057     0.000300     YES
 Maximum Displacement     0.000412     0.001800     YES
 RMS     Displacement     0.000137     0.001200     YES
 Predicted change in Energy=-2.989844D-07
 Optimization completed.

Frequencies:

 Low frequencies ---  -13.3559  -13.0443   -9.1055   -0.0110    0.0395    0.0599
 Low frequencies ---  288.9091  288.9205  403.4014

Aromaticity Investigation

Aromaticity is a property attributed to molecules that are:

cyclic
planar
contiguous, and
have 4n+2 π-electrons

Empirically, the behaviours of these compounds are dramatically different from their analogues of the same atomic arrangement, in particular displaying increased stability. Different models for molecular bonding offer different explanations for the properties of aromatic compounds. Consider the aromatic molecule benzene (C₆H₆):

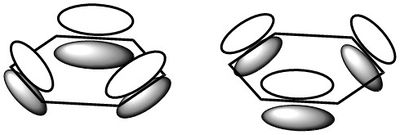
In valence bond theory, the 6 carbons form sp² hybridised orbitals, with two equatorial hybrid orbitals joining with neighbouring carbons (σ-bond), one hybrid orbital bonding with a hydrogen (σ-bond) and one p-orbital with one electron each orthogonal to the plane. The p-orbitals pair up to form π-bonds - this leads to the commonly known representation of benzene being a six-membered carbon ring with a double bond at every other carbon. The stability arises from the fact that the π-bonds can form one way or another, producing two structures that electrons can resonate between. The system is described as conjugated. One step further from this is the linear combination of all six in phase p-orbitals to form a large ring-like bonding orbital, which will give a volume where each of the one p-electron from the carbons can move freely as delocalised charges. Electrons are distributed over a wider space, rendering it more stable. This also accounts for other experimental facts such as evidence of ring current when the molecule is placed in a magnetic field, or electron densities above and below the ring.

Figure 3a: VBT model of benzene.
Figure 3b: 'Traditional' view of benzene bonding and resonance, giving rise to its stability.
Figure 3c: Delocalised π-electron model of benzene.

Finally using MO theory and quantum mechanics of conjugated systems set down by Hückle, a more complete picture of aromaticity can be illustrated. Not only are the p-orbitals combined, but when ever symmetry allows, other atomic orbitals present are also added together. The result from the simple linear combination of p-orbitals is observed, as well as out of phase anti-bonding molecular orbitals. This is used to further explain aromatic unique reactions, such as aromatic electrophilic substitutions and nucleophilic substitutions. In the following study, the aromatic nature of benzene and borazine as described by MO theory quantitatively computed by Gaussian is contrasted and compared. Borazine is also aromatic as all six atoms have p-orbitals orthogonal to the ring, with nitrogen providing all of the electrons into the delocalisation π-system.

Smf115 (talk) 17:24, 26 May 2018 (BST)Good discussion of the main concepts of aromaticity. Considering the benzene MO's visualised or more complex ideas of aromaticity, such as sigma-aromaticity, would help develop the discussion further.

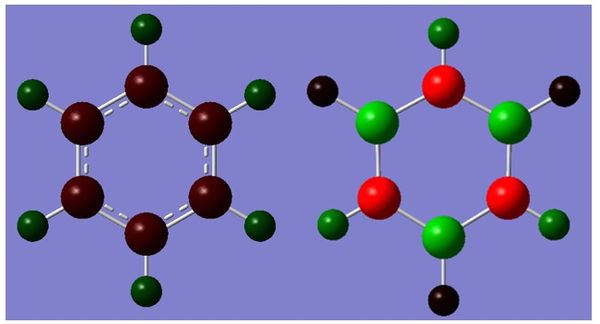
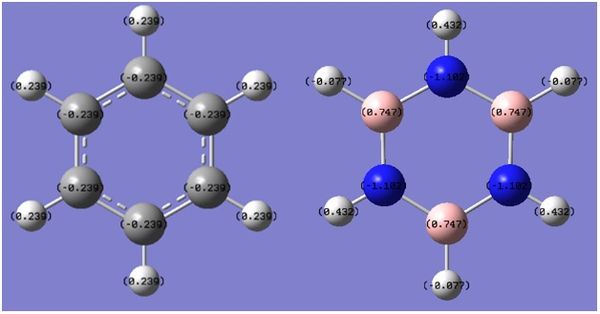
Charge Distribution

The distribution of charge as computed by Gaussian can be found below. The charge distribution of benzene is as expected: carbon is more electronegative and 'houses' the delocalised π-electrons, and is therefore more negative than hydrogen. The high order of symmetry means that charge is evenly distributed between all six C-H pairs. Borazine on the other hand has three species of different electronegativity. For instance nitrogen is very electronegative, hence when placed next to both hydrogen and boron it draws most of the electron density towards itself thus making it negative. Boron is less electronegative than hydrogen, so hydrogen attached draws a small amount of negative charge. The polarity between bonds in borazine have a much larger magnitude than benzene, due to the larger difference in electronegativity between respective species.

Figure
Figure

Molecular Orbitals

Smf115 (talk) 17:21, 26 May 2018 (BST)A good range of MOs selected with a thorough comparison given for each. Nice attempt at the corresponding LCAO diagrams too. To improve, when mentioning symmetry identify the symmetry label for the orbital or name the symmetry elements themselves, also energies between the molecules can't be compare, only the relative ordering of the MOs. Great answer with correct identification of charcter and orbital type though. Smf115 (talk) 17:22, 26 May 2018 (BST)Overall a good report with a strong project section and clear discussion throughout.

Orbital	Gaussian MO	LCAO	Description
π-type			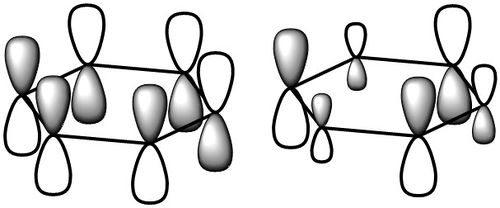This is one of the degenerate HOMO's of the system. It has some anti-bonding character, showing one nodal plane cutting through the ring. However the largely in phase combinations of solely p-orbitals above and below the plane of the ring with no hydrogen orbital contribution makes this a stabilised π-type bonding orbital. As expected, the more symmetrical benzene shows a more symmetrical 'gerade' orbital, whereas the borazine is lopsided, with large p contribution projecting from the nitrogen atoms and almost none from boron. This can be attributed to the greater electronegativity hence relative stability of nitrogen compared to boron, thus in a bonding orbital between the two, nitrogen will have a much larger contribution than boron. The borazine MO is stabilised by -0.28 hartree, whereas the benzene by -0.25. It would appear that the benzene HOMO is actually less stabilised (hence probably more reactive) than borazine. An interesting feature here is that larger lobes on nitrogen is consistent with the experimental observation[3] that aromatic electrophilic substitution, where electrons in this orbital donates to the LUMO of an electrophile, occurs preferentially at nitrogen, whereas no such selectivity is observed in benzene.
σ*-type		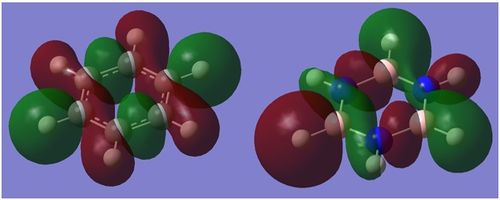	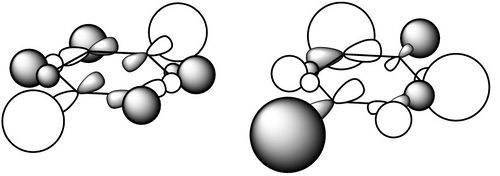This is one of the degenerate MO's just under the π-type described above. It is clearly σ-type as all the combinations are happening along the axis of bonds. All p-orbitals are parallel with the plane, and form four nodes, which then combine with equatorial hydrogens, notably with 'end' hydrogens contributing most to the overall MO. It has a mixture of bonding and antibonding character; for instance, the four nodal planes seem to cut through atoms instead of through bond (bonding), but it is also clearly complementary with a bonding pair lower in energy (not shown here), and through inspection of contributing LCAO shows phase cancellation. Overall it appears to be a populated high energy (benzene = 0.34 hartree, borazine = 0.32 hartree) antibonding σ-type orbital. The benzene is again more symmetrical with three planes of reflection as opposed to borazine which has two. Notice that the D_3h point group of borazine leads to a familiar orbital observed here: the doubly degenerate hydrogen chemical fragment for forming D_3h borane has two hydrogens in one phase and one in the other, just like the three large hydrogen lobes observed for the borazine here. Where there are large hydrogen lobes coincide with locations of borane atoms, also expected to have a larger contribution in anti-bonding than nitrogen.
σ-type		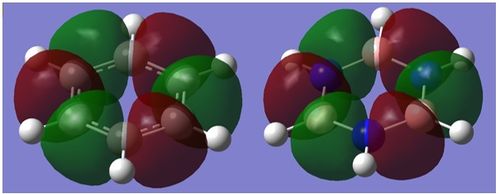	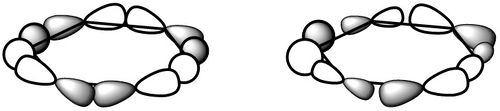This is a σ-type bonding MO found at -0.43 hartree for borazine and -0.44 hartree for benzene. This is very much a bonding orbital, with p-orbitals parallel to the plane of the ring along the bond axes combining in phase resulting in all nodes on atoms. These again appear to have no hydrogen contribution at all, and feels like the σ analogue of the first case. Although qualitative MO predicts larger lobes on the nitrogen by virtue of the MO's bonding nature, there is no observable distinction. Both MO's are very similar and equally symmetrical. Overall all the above show notable similarities, and hence will probably display similar aromatic properties.