Ggr07Module1:version1

Molecular Mechanics

The Hydrogenation of Cyclopentadiene Dimer

Thermodynamic evaluation of Endo and Exo Products

Endo and Exo Products

Properties	Exo	Endo
Total Energy (Kcal/mol)	34.0136	34.0153

It is known(reference) that the Endo product is specifically formed in this Diels-Alder reaction. Using Molecular Mechanics the stability of both isomers can be approximated and from this we can deduce whether the reaction is governed by thermodynamics or kinetics.

From the values obtained in table 1 it is seen that there is only marginal differences in relative energy between the two isomers. The Exo product is the thermodynamic product as it is slightly lower in energy. Knowning that the endo product is specifically formed in this reaction explains that this reaction is governed by it's kinetics.

Hydrogenation of Endo Product

The two possible mildly hydrogenated endo products

Properties	3	4
Stretch	1.2279	1.1366
Bend	18.6932	13.0252
Stretch-Bend	-0.7442	-0.564
Torsion	12.8241	12.4289
Non-Van der Waals	-1.3366	-1.3408
Van der Waals	6.039	4.4279
Dipole-Dipole	0.1632	0.141
Total Energy	36.8666	29.2548

Under mild hydrogenation conditions molecular mechanics can suggest the most stable dihydro product. It is known that under mild conditions one product is formed and after prolonged time the tetrahydro product is formed. This suggests that the kinetics initialy governs reactivity however the tetrahydro is formed after a prolonged amount of time showing that the activation energy barrier is obtainable under mild conditions for both alkenes.

In table 2 it is observed that all positive contributing aspects to the total energy are larger for product 3 than product 4. The non van der waals attractions are greater for product 4 (more negative). Therefore only the stretch-bend contribution is lower for product 3. This results in the overall energy of product three is comparetively far higher therefore it is the kinetic product initially formed. Then with time the second alkene bond is hydrogenated.

Stereochemistry of Nucleophilic additions to a pyridinium ring (NAD+ analogue)

First pyridinium derivative

The methylation of reagent 5

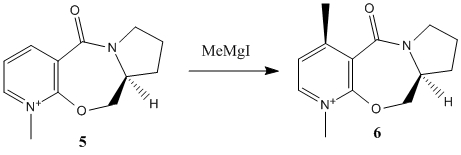
It is appreciated that only some atoms have been configured to run using Molecular Mechanics and thus the use of such elements as Mg (grignard reagents) is prohibited as calculations can not be computed with "unassigned atoms".

The Nucleophilic addition to a pyridinium ring can be analysed by the study of the confomer of the reactant. In the first example MM2 calculations can suggest the dihedral angle between the carbonyl bond and the pyridinium plane. It is worth noting that MM2 calculations are based on inputed parameters and therefore there is more than one minimum well which can be approached depending on the starting positions of atoms. By exploring different starting cartesian coordinates of atoms a range of carbonyl dihedral angles with low energy were discovered and the lowest energy geometry having the dihedral angle of 9⁰ being the closest approximation.

9⁰ of the dihedral angle of reagent 5

Properties	11 degrees	10 degrees	9 degrees	8 degrees
Total Energy	43.0827	43.0577	43.0512	43.0679

Second Pyridinium Derivative

The anilation of reagent 7

Another derivative of the pyridinium ring can be analysed to study the carbonyl dihedral bond angle. The values obtained are shown below. A common observation in both derivatives is that the carbonyl bond seems most stable when it is on the opposite side of the pyridinium ring to the stereospecific(proton in reactant) and methyl(in reactant 7).

In both reactions the approaching electrophile is on the opposite plane of the pyridinium ring in the product to the carbonyl bond. This can be rationalised as the electron rich oxygen of the carbonyl would deter a nucleophile from approach the pyridinium ring from this side.

Properties	-130 degrees	-21 degrees	-20 degrees	21 degrees	119 degrees	121 degrees
Total Energy (kcal/mol)	190.0599	63.4987	62.6549	63.4801	181.432	181.3535

Potential orientations of nucleophilic attack

It is worth noting that an improvement to the model would be the inclusion of the lone pair repulsion with other parts of the molecule.

Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol

Atropisomers of Taxinol

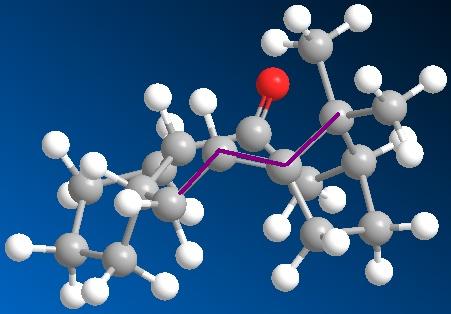
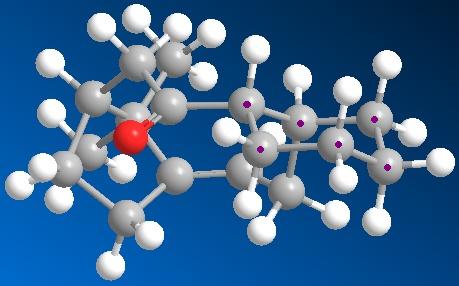
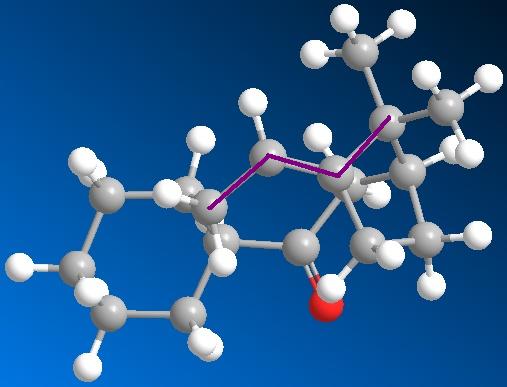
The application of MM2 can also be used for identifying Atropisomers and their relative stability. In taxinol there are two main atropisomer 9 has the carbonyl pointing upwards with the cyclohexane proton and the small bridge while 10 has the carbonyl pointing downwards relative to the proton and small bridge.

There are certain geometrical aspects of Taxol which can't be compromised during MM2 calculations to lower the energy.

1. The carbonyl has to be aligned vertical with respect to the small bridge and the indicated hydrogens
2. The hydrogens need to be both pointing upwards to retain stereochemistry at both centres
3. The alkene must maintain its E isomer geometry.
4. The conformation of the outer cyclohexane can vary.

As seen in table these conditions were met during MM2 calculations and the atropisomers energies are shown in table below. The observed more stable atropisomer of Taxol is 10 and also interestingly the outer cyclohexane adopts two different confomers to compensate for the carbonyl orientation with atropisomer 9 forming a twist-boat and 10 a chair conformation.

The Estimated Energy of the Atropisomers

	Geometry 9	Geometry 10
Energy (kcal/mol)	65.6793	53.2805
End Hexane	twist boat	chair

The important aspects of the conformations

Atropisomer	Carbonyl Position & protons conformation	Cyclohexane Conformation	Alkene isomer
9
10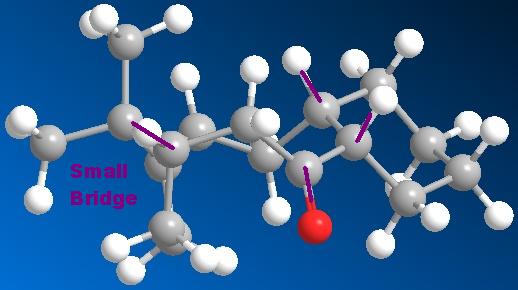

Semi-empirical Molecular Orbital Method

Until this point all calculations have been based purely on geometric conformations and their relative energy. However advanced computational calculations offers vaster and deeper applications in theoretical chmistry than just conformation analysis.

Using the calculation methods of MM2 solely it is possible to get a rough estimate of the geometry of a molecule. However this geometry can be fine tuned using semi-empirical calculations. In this example Mopac was used which is a programme which implements Semi-Empirical quantum chemistry Algorithms.

By considering the valence electron wavefunctions in Mopac calculations the geometry optimisation (via energy minimisation) can be improved but further a diagrammatic epresentation of the Molecular Orbitals of the molecule can be displayed. Further to these two calculations the geometry can be further optimised using a programe called Gaussian(9.0) and additionaly detailed predictions of bond stabilities can be correlated to IR stretches using the same programme.

Regioselective Addition of Dichlorocarbene

Predictions Using MM2 and MOPAC Calculations

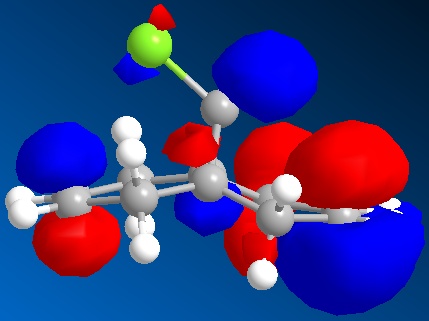
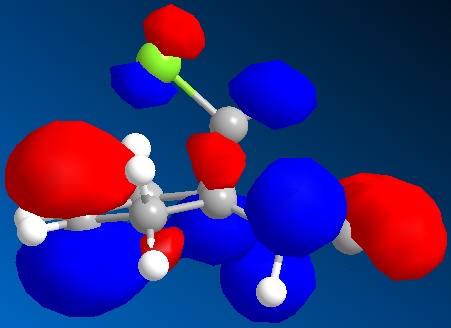
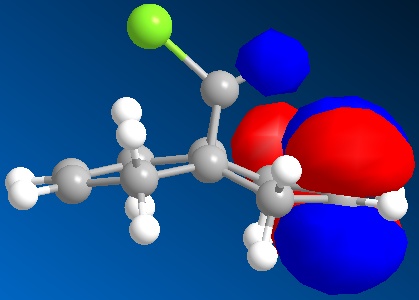
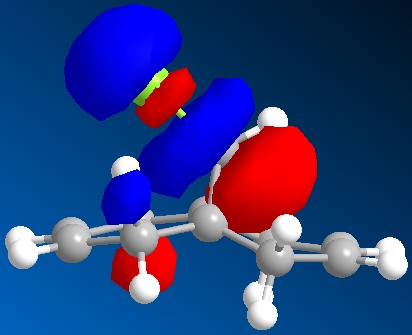
In this section we discuss the reactivity of the diene using theoretical computational methods. The rough approximation of the geometry was calculated using MM2 and then refined by consideration of the valence electrons wavefunctions. As described it is possible to display the Molecular Orbitals on the surface of the atoms. The HOMO and LUMO and one above and below are shown in the table below.

One key observation is that the position of the Cl in this rugged structure has large impact on the contributions of both alkenes to the molecules MO's.

The MO's of the Diene

HOMO-1	HOMO	LUMO	LUMO+1

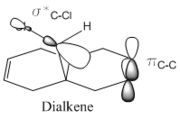
What can be extracted from these MO's is a comparison of both alkenes reactivity. If we were to hypothesise that a Dichlorocarbene were to react with this molecule then a prediction as to the more reactive alkene can be made. Knowing that the Dichlorocarbene is an electrophile the targeted MO is the molecules HOMO. In table it is observed that the alkene on the same side as the chlorine has a large contribution to the HOMO. Further the contribution of the anti alkene (alkene anti to the the C-Cl) to the HOMO is almost unapparent. Thus it can be deduced that the dichlorocarbene would most likely react at the alkene on the same side as the chlorine. It is however worth mentioning that the anti-alkene's contribution to the HOMO could increase in the product of this reaction due to molecules geometry change and could make the anti-alkene susceptible to another electrophile.

A possible interpretation as to the anti-alkene's surprising low contribution to the HOMO could be due to the constrained geometry. Under this geometry the σ*_C-Cl π_C-C are perfectly aligned for interaction. Therefore meaning that the electron density of the anti-alkene susceptible to nucleophilic attack is drawn away.

An image showing the angle with a dumy-bond

The Orbital Interactions

Corroborating with Gaussian Calculations

Absorption Frequencies (cm^-1)

	Diene	Monoene	DieneBH2
π C=C (Anti-Alkene)	1737.05	N/A	1657.18
π C=C (Same Side)	1757.44	1753.76	1756.55
σ C-Cl	770.83	779.93	759.05

The values collected in the table were calculated using Gaussian. This was done after initial MM2 and Mopac calculations on all structures.

The first thing to note is the anti-alkene has a lower frequency stretch. This indicates that lower energy is required to probe this bond and a lower energy means a weaker bond. This directly correlates with the findings that the bond is weakened (less reactive with nucleophiles). In the diene the σ_C-Cl bonds frequency is within the expected range(journal). Comparing it with the monalkene's σ_C-Cl at 779.93 we can see the diene's is stronger (higher frequency) as there is less electron density being donated to the σ* _C-Cl orbital which would destabilise it.

Monoene C=C stretch is approximately the frequency expected. It is expected to be similar to the diene and there is less than 4cm^-1 difference. The slight discrepancy might be due to the anti-alkene not apparent in the monene thus less constraints on the rings.

In order to further corroborate the data a BH2 unit was substitued for a H in the anti-alkene of the diene. This was intentionaly substituted. Boron is a more electropositive element than carbon but even so it is known to have many derivatives as useful synthetic Lewis acid. It is known that such Vinyllic Boroanes will attract electron density in to it's empty P_z orbital when the Boranes trigonal planar geometry is aligned parallel to the alkene. And this is shown to be the most stable geometry. It would be expected that the attraction of electron density will further weaken the anti-alkene C=C bond and less electron density will be available to donate in to the σ*_C-Cl therefore strengthening the σ_C-Cl relative to the non-substituted diene. And these observations are confirmed in terms of the frequencies stated.

Structure based Mini project using DFT-based Molecular orbital methods

Stereoselective synthesis of the hormonally active (25S)-D7-dafachronic acid,(25S)-D4-dafachronic acid, (25S)-dafachronic acid, and (25S)-cholestenoic acid via Evans Aldol Reaction

The reaction steps proposed for forming the intermediate and followed by the synthesis of the first acid

This published journal states the stereoselective and regioselective isomers described in the title. It was chosen as potential reactivity to be studied for many reason.

1. The journal is based on the successful synthesis of all of these acids and have a regioselective and stereoselective aspect.
2. The carbon framework is quite rigid due to the steroid backbone of the structures.
3. The regio and stereoselective attributes of the acids to be investigated are all apparent in one key intermediate.
4. And finally the stereo and regioselective aspects both happen in one step.

What can therefore be extrapolated from these points is that if we assume that the following reactivity of the intermediate to the acids can't effect the regio/stereo selective outcome then comparing one products spectroscopic data is enough to confirm the validity of all other acids.

Therefore the first acid is chosen to be the focus of study.

Stereoselective - Using an Evans Oxazolidinone auxiliary

The Aldol reaction which would give a racemic mixture of products.

The stereoselective chemistry of this synthesis is defined as whether the methane group becomes R or S during the reaction. If the reaction was followed directly by adding base, a racemic mixture of products would be expected as shown.

One method of proceeding with the aldol reaction stereoselectivly is by FGI in which the aldehyde is converted in to an Evans auxiliary.

The Evans Carbonyl Auxiliary

By forming this auxiliary one side of the enolates "alkene" is stericaly hindered by the isopropyl group and thus depending on the stereochemistry of the isopropyl group the nucleophile will attack at the opposite side. A 3D applet is provided to show the steric hinderence of the enol alkene by the isopropyl group.

Evans Carbonyl Auxiliary

Unfortunately the optical rotation or Circular Dichroism were not supplied in the journal.

As these are diastereoisomers and vary only at one chiral centre and not enantiomers we would expect them to have the same sign (+/-) with a slight variance in the angle (as opposed to enantiomers which are the same angle of opposite sign).

Note - Due to the vast number of heavy-atoms in the molecule the Conformation optimisation of the two isomers over ran the maxcycle=25 stated and therefore produced errors. However the log output files are readable and therefore the optimised geometry had been submitted for a 2nd attempt at Optical Rotation calculations but was unsucessful.

Regioselective - Cross-Aldols

Aldol reactions are known to have issues with regioselectivity as their is the potential for both compounds to enolise therefore giving regioselective issues. Depicted is the undesired product which can be formed if the steroid forms the enolate.

The cross-aldol reaction giving an undesired product

By adding Bu₂BOTf the Evan's auxiliary is favoured for enolisation rather than the aldehyde due to kinetically controled steps.

The Boron forms the enol with high reactivity towards the steroids aldehyde and proceeds through to give the regioselective product.

If it were to be hypothesised that the regioselectivity does not occur with such high yields or indeed only the undesired product is formed then carbon NMR could be used to distinguish between the two regioisomers.

The two regioisomers which would show a slight variance in the C13 NMR spectrum.

Note - As for previous section due to the vast number of heavy-atoms in the molecule the Conformation optimisation of the two isomers over ran the maxcycle=25 stated and therefore produced errors. However the log output files are readable and therefore the optimised geometry has been applied for a 2nd attempt at NMR calculations.

C13 NMR Spectrum of Suggested Product 1

The Difference between the journal and calculated value of the ¹³C NMR

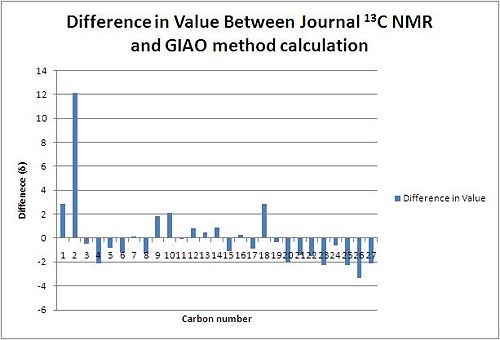
C13 NMR Chemical Shift (δ) of Suggested Product 1
Journal Values	Calculated Values	Difference	sqrt((Value)^2)	< 5		Standard Deviations	Below 1
212.17	209.316	2.854	2.854	TRUE		1.427	FALSE
182.55	170.401	12.149	12.149	FALSE		6.0745	FALSE
139.48	139.976	-0.496	0.496	TRUE		0.248	TRUE
117	119.104	-2.104	2.104	TRUE		1.052	FALSE
56.02	56.8396	-0.8196	0.8196	TRUE		0.4098	TRUE
54.9	56.1321	-1.2321	1.2321	TRUE		0.61605	TRUE
48.81	48.7028	0.1072	0.1072	TRUE		0.0536	TRUE
44.22	45.5189	-1.2989	1.2989	TRUE		0.64945	TRUE
43.35	41.534	1.816	1.816	TRUE		0.908	TRUE
42.83	40.6968	2.1332	2.1332	TRUE		1.0666	FALSE
39.4	39.479	-0.079	0.079	TRUE		0.0395	TRUE
39.36	38.5149	0.8451	0.8451	TRUE		0.42255	TRUE
38.75	38.2866	0.4634	0.4634	TRUE		0.2317	TRUE
38.11	37.221	0.889	0.889	TRUE		0.4445	TRUE
36.04	37.1449	-1.1049	1.1049	TRUE		0.55245	TRUE
35.68	35.4283	0.2517	0.2517	TRUE		0.12585	TRUE
34.38	35.2939	-0.9139	0.9139	TRUE		0.45695	TRUE
34.01	31.1287	2.8813	2.8813	TRUE		1.44065	FALSE
30.04	30.3898	-0.3498	0.3498	TRUE		0.1749	TRUE
27.92	29.9867	-2.0667	2.0667	TRUE		1.03335	FALSE
23.79	25.2169	-1.4269	1.4269	TRUE		0.71345	TRUE
22.92	24.4107	-1.4907	1.4907	TRUE		0.74535	TRUE
21.68	23.9405	-2.2605	2.2605	TRUE		1.13025	FALSE
18.74	19.3722	-0.6322	0.6322	TRUE		0.3161	TRUE
17.01	19.2379	-2.2279	2.2279	TRUE		1.11395	FALSE
12.45	15.8117	-3.3617	3.3617	TRUE		1.68085	FALSE
11.89	13.9978	-2.1078	2.1078	TRUE		1.0539	FALSE

From reading the table it can be seen that all (apart for one) calculated values of the carbon chemical shifts are within 5(ppm) of the journal values. The value of Carbon 27 with a predicted frequency of 170.401 is the only value above 5ppm different to the journal. This can be attributed to the spin-orbit coupling error (that arrises with ester,amide carboxylic acid type bonds) and thus the value must be scaled using the factor of δ_corr=0.96δ_Calc+12.2 giving a corrected value of δ=175.78 which has a difference from the journal of Δδ=6.77. This is still larger than five. Judging from the standard deviations of all the other carbon atoms of the suggested product 1 it is unlikely that the assigned regioselectivity of the journal is incorrect and further the carboxylic acid deviance from the journal value could be contributed to a factor of inaccuracy of the correction factor for carboxylic acids and the slight discrepancy in conformation as the minimum energy conformation of the product 1 might not have been reached.