First steps with ONIOM : excited state of Bicyclo(10,2,2)Hexadeca-1(15),12(16)13-triene
Introduction
In order to introduce the ONIOM methodology some calculations will be run on BICYCLO(10.2.2)HEXADECA-1(15),12(16),13-TRIENE
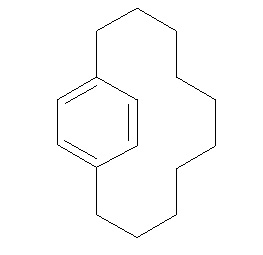
Ultimately, we wish to include a CASSCF calculation in the high level of theory in order to optimize the ground state. This can then be used to explore the first excited state of the molecule and find any points of interest on the potential energy surface (PES). In this example AM1 will be used for the low level model.
Advice break
First read the parts Introduction, and First steps with ONIOM
First, draw the molecule as below, then select the high and low layers as was done in the previous tutorial. The high layer should include the benzene ring, and the environment should be in the low layer.
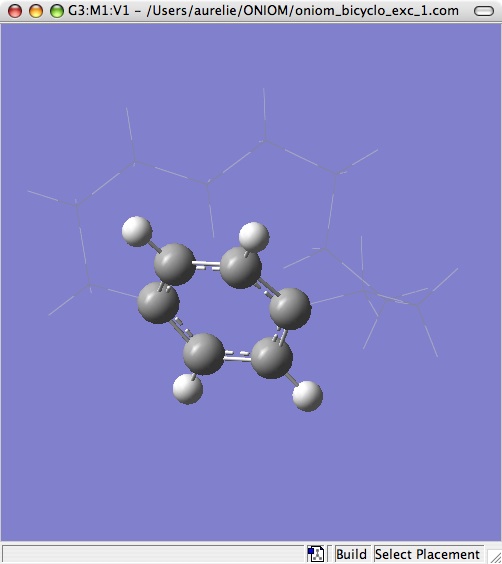
The orbitals
Advice break
Before beginning this part make sure that you read the part ONIOM for excited states.
We need initial orbitals for the CASSCF computation. The active orbitals shall be chosen from these molecular orbitals.
Calculation
In order to specify the correct orbitals for the CASSCF active space they must be calculated on the high model separately and then read these back into the ONIOM calculation. This is done using the onlyinputfiles option. It is important to use the nosymm keyword in the route section so that the molecular specification is consistent throughout. The first calculation was carried out on the STO-3G basis set using Hartree-Fock theory and then the size of the basis set was increased to 4-31G.
#p oniom(RHF/STO-3G:am1)=onlyinputfiles pop=full nosymm
Results
The output gives the three parts of the ONIOM calculation as three separate input files. The high model input can then be used to calculate initial orbitals at the STO-3G level.
#P Test IOp(2/15=1,5/32=2,5/38=1) RHF/STO-3G
sto3g starting orbital calc of bchdt
Point 2 -- high level on model system.
0 1
H(Iso=12) 0.243857585655 1.123532208217 1.625607623259
Bq-#1(Iso=1.00782504,Spin=1,GFac=2.792846) 0.365994000000 0.235394000000 0.711838000000
Bq-#1(Iso=1.00782504,Spin=1,GFac=2.792846) -0.935727000000 0.660481000000 1.789731000000
Bq-#1(Iso=12) -0.323129000000 2.285691000000 0.484179000000
Bq-#1(Iso=1.00782504,Spin=1,GFac=2.792846) -0.702530000000 3.047859000000 1.132295000000
Bq-#1(Iso=1.00782504,Spin=1,GFac=2.792846) -1.048587000000 2.060305000000 -0.269354000000
Bq-#1(Iso=12) 0.983896000000 2.798525000000 -0.203538000000
Bq-#1(Iso=1.00782504,Spin=1,GFac=2.792846) 1.332005000000 2.051805000000 -0.886275000000
Bq-#1(Iso=1.00782504,Spin=1,GFac=2.792846) 0.772907000000 3.702462000000 -0.735781000000
Bq-#1(Iso=12) 2.093084000000 3.060075000000 0.850709000000
Bq-#1(Iso=1.00782504,Spin=1,GFac=2.792846) 2.278899000000 2.141164000000 1.366436000000
Bq-#1(Iso=1.00782504,Spin=1,GFac=2.792846) 1.774786000000 3.806383000000 1.548284000000
Bq-#1(Iso=12) 3.415381000000 3.524574000000 0.158930000000
Bq-#1(Iso=1.00782504,Spin=1,GFac=2.792846) 3.295725000000 4.491963000000 -0.282365000000
Bq-#1(Iso=1.00782504,Spin=1,GFac=2.792846) 3.670954000000 2.817601000000 -0.602497000000
Bq-#1(Iso=12) 4.543434000000 3.528876000000 1.220662000000
Bq-#1(Iso=1.00782504,Spin=1,GFac=2.792846) 5.495493000000 3.727181000000 0.774388000000
Bq-#1(Iso=1.00782504,Spin=1,GFac=2.792846) 4.367924000000 4.260174000000 1.981779000000
Bq-#1(Iso=12) 4.456281000000 2.127451000000 1.796023000000
Bq-#1(Iso=1.00782504,Spin=1,GFac=2.792846) 3.479403000000 2.046995000000 2.225133000000
Bq-#1(Iso=1.00782504,Spin=1,GFac=2.792846) 4.574031000000 1.434144000000 0.989574000000
Bq-#1(Iso=12) 5.463634000000 1.714145000000 2.887830000000
Bq-#1(Iso=1.00782504,Spin=1,GFac=2.792846) 5.108574000000 0.758074000000 3.211499000000
Bq-#1(Iso=1.00782504,Spin=1,GFac=2.792846) 6.456876000000 1.631187000000 2.498615000000
Bq-#1(Iso=12) 5.526159000000 2.646486000000 4.124035000000
Bq-#1(Iso=1.00782504,Spin=1,GFac=2.792846) 5.836259000000 2.016484000000 4.931399000000
Bq-#1(Iso=1.00782504,Spin=1,GFac=2.792846) 6.221698000000 3.449776000000 3.998138000000
H(Iso=12) 3.852485354805 3.091818942897 4.262001608287
Bq-#1(Iso=1.00782504,Spin=1,GFac=2.792846) 4.114326000000 3.568051000000 5.434101000000
Bq-#1(Iso=1.00782504,Spin=1,GFac=2.792846) 4.123134000000 4.212585000000 3.804036000000
C 3.003688000000 2.488547000000 3.914278000000
C 2.972790000000 1.096362000000 3.761867000000
C 1.918003000000 3.272905000000 3.546773000000
C 1.938222000000 0.548655000000 2.964640000000
H 3.717611000000 0.472056000000 4.209510000000
C 0.910010000000 2.742444000000 2.788282000000
H 1.880394000000 4.301750000000 3.838260000000
C 0.975169000000 1.418853000000 2.399498000000
H 1.893799000000 -0.504464000000 2.780608000000
H 0.086018000000 3.353573000000 2.484210000000
The input file created by the inputfilesonly option, shown above, contains a number of ghost atoms. It is not known the exact purpose of these, however, it appears that they act as 'place-holders' for the other atoms in the system that are outside the specific part of the model being calculated. Indeed, if they are not used then, when the orbitals are fed into the full ONIOM calculation, an error message is obtained:
Unable to project occupied orbitals !
Initial Orbitals
A single point energy calculation can be carried out using the above input file, remembering to use the nosymm keyword. Once the single point energy calculation with the STO-3G basis set has been carried out, these orbitals can be used to calculate a single-point energy with a 4-31G basis set, using the guess=read keyword.
Visualize the orbitals
The correct CASSCF active space must be specified in the relevant checkpoint file prior to the ONIOM calculation. This can be done using the orbitals from the RHF/4-31g single point energy calculation in conjunction with the guess=alter keyword to obtain a CASSCF/6-31g* single point energy calculation.
By visualizing the orbitals in GaussView it can be determined that the relevant molecular orbitals are 17, 20, 21, 22, 23, 30. A new input file can then be constructed to obtain the correct CAS space, so that the correct orbitals have been swapped into it. The correct input file should appear, therefore, as below:
%chk=/work/lmt09/bchdt/cas631gd_full_mo_2
%mem=800mb
#P Test IOp(2/15=1,5/32=2,5/38=1) CAS(6,6)/6-31G(d) guess=(read,alter) geom=check pop=full nosymm
631gd starting orbital calc of bchdt
Point 2 -- high level on model system.
0 1
17 19
24 30
Input and output files
Media:oniom_rhfsto3g_am1_inputfile_nosymm.log
Media:rhfsto3g_full_mo_nosymm.log
Media:rhf431g_full_mo_2.log
Media:cas631gd_full_mo_2.log
Oniom Ground State Optimization
Calculation
The correctly ordered active space is now held in the checkpoint file of the CASSCF(6,6)/6-31G* single point energy calculation. This must now be read in using the guess=input keyword. The checkpoint file must be specified below the molecule coordinate data so that it is in the following order:
Low Real
High Model
Low Model
The low model and low real systems have not been calculated in this example and so generate must be put so that these are calculated during the oniom calculation
#p oniom(CAS(6,6)/6-31G(d):am1) guess=input nosymm pop=full opt ''Molecular Specification'' generate /work/lmt09/bchdt/cas631gd_full_mo_2.chk generate
NOTE: Gaussian versions previous to GDV H08 require the orbital files to be entered on consecutive lines so if you receive an error message relating to blank lines or otherwise this may be due to how these are entered in the input file. Further information can be found at the bottom of the ONIOM user reference.
Results
The output should indicate that the high model initial orbitals have optimized within a few iterations, indicating that these have been read in correctly from the checkpoint file. The calculation should converge in 41 steps giving the following energies:
ONIOM: calculating energy. ONIOM: gridpoint 1 method: low system: model energy: 0.039218019520 ONIOM: gridpoint 2 method: high system: model energy: -230.774789631291 ONIOM: gridpoint 3 method: low system: real energy: -0.049880009326 ONIOM: extrapolated energy = -230.863887660137
Input and output files
Media:oniom_cas631gd_am1_opt_2.gjf
Media:oniom_cas631gd_am1_opt_2.log
Calculate the S1 Franck-Condon vertical excitation energy
Calculation
The vertical excitation energies can be calculated from this optimised geometry. The force keyword can be used to provide information about the gradient of the potential energy surface at this geometry.
Keyword break
You must include nroot=x in the CAS keyword ==> Calculations on excited states of molecular systems may be requested using the NRoot option. (Note that a value of 1 specifies the ground state, not the first excited state)
#p oniom(CAS(6,6,nroot=2)/6-31G(d):am1) guess=read geom=check force nosymm pop=full
Results
Advice break
When calculating an energy difference between two states it is important to use the same basis set that was used to print the orbitals for the optimized ground state of the molecule.
You should get this energy in the output file. Ensure that the orbitals have converged within a few iterations so that we know they have been read in correctly.
ONIOM: calculating energy. ONIOM: gridpoint 1 method: low system: model energy: 0.039218019520 ONIOM: gridpoint 2 method: high system: model energy: -230.593515342634 ONIOM: gridpoint 3 method: low system: real energy: -0.049880009324 ONIOM: extrapolated energy = -230.682613371479
The difference between the energy of the excited state and the ground state is:
ΔE = ES1FC - ES0min = (-230.68261) - (-230.86389) = 0.18127 Har = 113.75 Kcal mol-1
Input and output files
Media:oniom_nroot2_cas631gd_am1_fc_dir.gjf
Media:oniom_nroot2_cas631gd_am1_fc_dir.log
Optimize the S1 minimum
Calculation
We will optimize the minimum on the S1 to be able to give the energy difference between the S1 minimum and the conical intersection.
#p oniom(casscf(6,6,nroot=2)/6-31g(d):am1) geom=check Guess=read nosymm pop=full opt
Results
The geometry optimizes in 11 steps with this geometry :
Input orientation:
---------------------------------------------------------------------
Center Atomic Atomic Coordinates (Angstroms)
Number Number Type X Y Z
---------------------------------------------------------------------
1 6 0 -0.397359 1.509315 1.703924
2 1 0 -0.432226 0.447000 1.337085
3 1 0 -1.392518 1.722582 2.184654
4 6 0 -0.239846 2.435995 0.506433
5 1 0 -0.330737 3.499987 0.851183
6 1 0 -1.096600 2.238934 -0.191836
7 6 0 1.065374 2.251667 -0.246153
8 1 0 1.445215 1.207509 -0.088833
9 1 0 0.882412 2.374662 -1.346028
10 6 0 2.117507 3.248383 0.196432
11 1 0 2.175856 3.234268 1.319725
12 1 0 1.801000 4.282972 -0.100125
13 6 0 3.486247 2.954955 -0.385458
14 1 0 3.574340 3.439175 -1.393106
15 1 0 3.612447 1.850879 -0.539702
16 6 0 4.595463 3.464365 0.517914
17 1 0 5.532928 3.598957 -0.082608
18 1 0 4.313296 4.474335 0.916714
19 6 0 4.863430 2.506758 1.662173
20 1 0 3.909598 1.980824 1.943231
21 1 0 5.583962 1.715919 1.324675
22 6 0 5.414016 3.200554 2.891729
23 1 0 6.442359 3.587508 2.665657
24 1 0 4.774424 4.087958 3.142193
25 6 0 5.477464 2.266800 4.086731
26 1 0 5.573918 1.206157 3.733289
27 1 0 6.396688 2.501584 4.687019
28 6 0 4.277815 2.374278 5.017766
29 1 0 4.425555 1.649431 5.866112
30 1 0 4.259951 3.404760 5.467312
31 6 0 2.999475 2.093391 4.351312
32 6 0 2.741107 0.794121 3.782971
33 6 0 2.012118 3.132321 4.201999
34 6 0 1.592039 0.584429 2.953048
35 1 0 3.447729 -0.001227 3.927629
36 6 0 0.849471 2.914428 3.393373
37 1 0 2.168143 4.089945 4.662020
38 6 0 0.670414 1.663055 2.700639
39 1 0 1.442771 -0.369114 2.482431
40 1 0 0.142500 3.709566 3.249263
hexadiene_anti |
And this energy :
ONIOM: calculating energy. ONIOM: gridpoint 1 method: low system: model energy: 0.054177360561 ONIOM: gridpoint 2 method: high system: model energy: -230.599106815981 ONIOM: gridpoint 3 method: low system: real energy: -0.037302631996 ONIOM: extrapolated energy = -230.690586808537
Input and output files
Media:oniom_nroot2_cas631gd_am1_opt_dir.gjf
Media:oniom_nroot2_cas631gd_am1_opt_dir.log
Find the S1/S0 conical intersections
Advice break
Before beginning this part make sure that you read the part ONIOM for crossings.
In order to find the conical intersection we will start from the Franck-Condon geometry. As was done in the CASSCF tutorial, the planar structure of the benzene ring must be broken by moving one of the carbon atoms out of the plane. The molecule has C2 symmetry so there are three possible carbon atoms to move out the plane. This suggests that there may be multiple different S1/S0 crossings that can be located by the conical intersection optimization.
Calculation
In order to locate a conical intersection the Opt=conical option must be specified.
#p oniom(CAS(6,6,nroot=2)/6-31g(d):am1) guess=read nosymm pop=full opt=conical
In the versions of Gaussian prior to GDVH08 (G09A.02 and GDVH01) there is a bug which results in the low level parts of the molecule not being included in the gradient calculation. Until this is resolved the route must be modified. This can be done by using the testrt command and then inputting the above route when requested. The non-standard route must then be copied and pasted into the input file and appended with the bold type as below:
# nonstd 1/9=11,11=1,14=-1,18=20,19=9,26=1,38=1,52=2/1,3; 2/9=110,12=2,15=1,17=6,18=5,40=1/2; 1/9=11,11=1,14=-1,18=20,19=9,38=1,52=2,53=3172/20; 3/5=2,16=1,25=1,41=700000,71=1,116=-2/1,2,3; 4/5=1,17=6,18=6,35=1/1; 5/5=2,17=30000000,35=1,38=6/2; 6/7=3,28=1/1; 7/7=1,30=1,33=-1/1,2,3,16; <========================== 1/9=11,11=1,14=-1,18=20,19=9,52=2,53=2032/20; 3/5=1,6=6,7=1,16=1,25=1,32=1,71=1,116=101/1,2,3; 4/5=1,17=6,18=6/1,5; 5/5=2,17=31000200,28=2,38=6/10; 8/6=4,10=90,11=11/1; 11/31=1,42=1,45=1/1; 10/10=900005,28=2,31=1/3; 6/7=3/1; 7/7=1,30=1,33=-1/16; 1/9=11,11=1,14=-1,18=20,19=9,52=2,53=1022/20; 3/5=2,16=1,25=1,41=700000,71=1,116=-2/1,2,3; 4/5=1,17=6,18=6,35=1/1; 5/5=2,17=30000000,35=1,38=6/2; 6/7=3,28=1/1; 7/7=1,30=1,33=-1/1,2,3,16; <=========================== 1/9=11,11=1,14=-1,18=20,19=9,52=2,53=3015/20; 7/9=1,44=-1/16; 1/9=11,11=1,14=-1,18=20,19=9,52=2/3(2); 2/9=110,15=1/2; 99//99; 2/9=110,15=1/2; 1/9=11,11=1,14=-1,18=20,19=9,52=2,53=3173/20; 3/5=2,16=1,25=1,41=700000,71=1,135=20/1,2,3; 4/5=5,16=3,17=6,18=6,35=1/1; 5/5=2,17=30000000,35=1,38=5/2; 7/7=1,30=1,33=-1/1,2,3,16; <=========================== 1/9=11,11=1,14=-1,18=20,19=9,52=2,53=2033/20; 3/5=1,6=6,7=1,16=1,25=1,32=1,71=1,116=101/1,2,3; 4/5=5,16=3,17=6,18=6/1,5; 5/5=2,17=31000200,23=1,28=2,38=5/10; 8/6=4,10=90,11=11/1; 11/31=1,42=1,45=1/1; 10/10=900005,28=2,31=1/3; 7/7=1,30=1,33=-1/16; 1/9=11,11=1,14=-1,18=20,19=9,52=2,53=1023/20; 3/5=2,16=1,25=1,41=700000,71=1,135=20/1,2,3; 4/5=5,16=3,17=6,18=6,35=1/1; 5/5=2,17=30000000,35=1,38=5/2; 7/7=1,30=1,33=-1/1,2,3,16; <=========================== 1/9=11,11=1,14=-1,18=20,19=9,52=2,53=3015/20; 7/9=1,44=-1/16; 1/9=11,11=1,14=-1,18=20,19=9,52=2/3(-21); 2/9=110,15=1/2; 99//99;
Results
Three different conical intersection (CI) geometries can be found to exist by comparison of the extrapolated energies for the completed CI optimization. An image of each CI geometry and its energy is given below:
CIUP1: Optimized in 23 steps
hexadiene_anti |
and with the following energy:
ONIOM: calculating energy. ONIOM: gridpoint 1 method: low system: model energy: 0.211163466995 ONIOM: gridpoint 2 method: high system: model energy: -230.569085296465 ONIOM: gridpoint 3 method: low system: real energy: 0.112316208274 ONIOM: extrapolated energy = -230.667932555186
ΔE = ECIUP1 - ES1min = (-230.56909) - (-230.69059) = 0.02265 Har = 14.22 Kcal mol-1
CIUP3: Optimized in 54 steps
hexadiene_anti |
and with the following energy:
ONIOM: calculating energy. ONIOM: gridpoint 1 method: low system: model energy: 0.222741936300 ONIOM: gridpoint 2 method: high system: model energy: -230.562330862710 ONIOM: gridpoint 3 method: low system: real energy: 0.144329339459 ONIOM: extrapolated energy = -230.640743459551
ΔE = ECIUP3 - ES1min = (-230.64074) - (-230.69059) = 0.04985 Har = 31.28 Kcal mol-1
CIDOWN3: Optimized in 28 steps
hexadiene_anti |
and with the following energy:
ONIOM: calculating energy. ONIOM: gridpoint 1 method: low system: model energy: 0.216660845836 ONIOM: gridpoint 2 method: high system: model energy: -230.569464938114 ONIOM: gridpoint 3 method: low system: real energy: 0.122156322610 ONIOM: extrapolated energy = -230.663969461340
ΔE = ECIDOWN3 - ES1min = (-230.66397) - (-230.69059) = 0.02662 Har = 16.70 Kcal mol-1
CIDOWN1: Optimized in 32 steps
hexadiene_anti |
and with the following energy:
ONIOM: calculating energy. ONIOM: gridpoint 1 method: low system: model energy: 0.227957830383 ONIOM: gridpoint 2 method: high system: model energy: -230.560046131581 ONIOM: gridpoint 3 method: low system: real energy: 0.147593210079 ONIOM: extrapolated energy = -230.640410751885
ΔE = ECIDOWN1 - ES1min = (-230.64041) - (-230.69059) = 0.05018 Har = 31.49 Kcal mol-1
CIDOWN2: Optimized in 32 steps
hexadiene_anti |
and with the following energy:
ONIOM: calculating energy. ONIOM: gridpoint 1 method: low system: model energy: 0.216199244003 ONIOM: gridpoint 2 method: high system: model energy: -230.569023708297 ONIOM: gridpoint 3 method: low system: real energy: 0.123880540105 ONIOM: extrapolated energy = -230.661342412195
ΔE = ECIDOWN2 - ES1min = (-230.66134) - (-230.69059) = 0.02925 Har = 18.35 Kcal mol-1
Input and output files
Media:oniom_nroot2_cas631gd_am1_con_dira.gjf
Media:oniom_nroot2_cas631gd_am1_con_dir.log
Media:oniom_nroot2_cas631gd_am1_con_alt1.log
Media:oniom_nroot2_cas631gd_am1_con_alt2.log
Media:oniom_nroot2_cas631gd_am1_con_alt3.log
Comparison of ONIOM with Alternative Methods
In order to demonstrate the extent to which ONIOM agrees with alternative methods, the ΔE values, chromophore geometry and frequencies have been compared to benzene in isolation and the whole molecule calculated at the CAS(6,6)/6-31G* level.
ΔE Values
| ΔE / Kcal mol-1 | ONIOM | benzene | full molecule |
|---|---|---|---|
| ES1FC - ES0min | 113.75 | 113.27 | 112.83 |
| EFCS1 - ES1min | 5.00 | 3.02 | 4.98 |
| ECIUP1 - ES1min | 14.22 | 19.09 | 15.40 |
| ECIUP2 - ES1min | N/A | N/A | 37.32 |
| ECIUP3 - ES1min | 31.28 | N/A | N/A |
| ECIDOWN1 - ES1min | 31.49 | N/A | 37.92 |
| ECIDOWN2 - ES1min | 18.35 | N/A | 17.56 |
| ECIDOWN3 - ES1min | 16.70 | N/A | N/A |
The effect of the aliphatic chain can be determined by the above figures to increase the energy difference between the S1 minimum and the conical intersection. This is because as the chromophore bends upwards, the interactions between it and the aliphatic chain increase. This also explains the greater difference between CIUP1 and CIUP2/ CIUP3, as the chromophore is bent into closer proximity in the later two CIs.
Chromophore Geometry
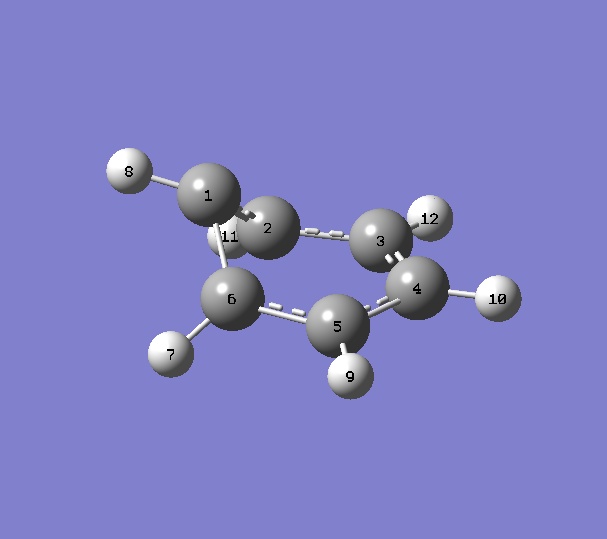
ONIOM CIUP1
| Atom | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 1 | -X- | ||||
| 2 | 1.4542 | -X- | |||
| 3 | 2.5364 | 1.4662 | -X- | ||
| 4 | 2.9474 | 2.4209 | 1.3948 | -X- | |
| 5 | 2.5362 | 2.5773 | 2.3257 | 1.3947 | -X- |
| 6 | 1.4540 | 1.9316 | 2.5773 | 2.4211 | 1.4664 |
benzene
| Atom | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 1 | -X- | ||||
| 2 | 1.4543 | -X- | |||
| 3 | 2.5368 | 1.4664 | -X- | ||
| 4 | 2.9480 | 2.4212 | 1.3949 | -X- | |
| 5 | 2.5368 | 2.5776 | 2.3260 | 1.3949 | -X- |
| 6 | 1.4543 | 1.9322 | 2.5777 | 2.4213 | 1.4664 |
Full molecule
| Atom | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 1 | -X- | ||||
| 2 | 1.4762 | -X- | |||
| 3 | 2.5465 | 1.4788 | -X- | ||
| 4 | 2.9640 | 2.4502 | 1.4131 | -X- | |
| 5 | 2.5474 | 2.5949 | 2.3439 | 1.4112 | -X- |
| 6 | 1.4784 | 1.9397 | 2.5936 | 2.4473 | 1.4766 |
Frequencies
These are analysed here
IOP keyword
There are many IOp keywords, and here we can use IOp(1/33=1). This keyword indicates that we want to get back the geometry of the target molecule in this ONIOM calculation, and so not only get back the geometry of the real molecule.
#p oniom(casscf(6,6)/6-31g(d):am1) Guess=read nosymm IOp(1/33=1)
So, thanks to this keyword, the geometry of the target molecule is the following :
ONIOM: restoring gridpoint 1 on chk file.
ONIOM: generating point 1 -- low level on model system.
At end of L120:
---------------------------------------------------------------------
Center Atomic Atomic Coordinates (Angstroms)
Number Number Type X Y Z
---------------------------------------------------------------------
1 1 0 2.638717 4.881571 1.665528
2 1 -1 2.020669 3.806841 2.119983
3 1 -1 1.564638 5.088371 0.929869
4 6 -1 3.314030 3.943445 0.389290
5 1 -1 3.584379 4.705053 -0.389281
6 1 -1 2.699570 3.153485 -0.119072
7 6 -1 4.577518 3.310210 0.944654
8 1 -1 4.425122 3.058103 2.027696
9 1 -1 4.780995 2.347863 0.405654
10 6 -1 5.778946 4.223227 0.800534
11 1 -1 5.512725 5.234946 1.213375
12 1 -1 6.011110 4.366215 -0.287617
13 6 -1 7.009661 3.696294 1.512628
14 1 -1 7.588584 3.035757 0.815342
15 1 -1 6.709064 3.063651 2.388981
16 6 -1 7.903617 4.826480 1.993550
17 1 -1 8.948652 4.442296 2.127550
18 1 -1 7.946627 5.624976 1.206684
19 6 -1 7.409836 5.408652 3.303756
20 1 -1 6.293275 5.290111 3.368030
21 1 -1 7.848762 4.828586 4.157713
22 6 -1 7.750705 6.877079 3.462777
23 1 -1 8.863562 6.988595 3.547120
24 1 -1 7.429483 7.438715 2.545653
25 6 -1 7.087576 7.483957 4.686597
26 1 -1 6.880832 6.679877 5.441567
27 1 -1 7.794562 8.213303 5.164295
28 1 0 5.642638 7.961321 4.163574
29 1 -1 5.361452 8.598202 5.364997
30 1 -1 6.037749 9.149773 3.782291
31 6 0 5.232283 7.237539 3.559949
32 6 0 4.265206 6.282722 4.297471
33 6 0 4.457125 7.660606 2.321484
34 6 0 3.439064 5.381387 3.596924
35 1 0 4.501131 6.078114 5.327092
36 6 0 3.650875 6.777430 1.632915
37 1 0 4.862797 8.527096 1.829134
38 6 0 3.163893 5.610494 2.240833
39 1 0 3.055582 4.500581 4.081594
40 1 0 3.429852 6.972394 0.598125
The indication -1 corresponds to a frozen atom, i.e. an atom which is not include in the model.
Break advice
If you want to make some calculation just on the model part you can take back the geometry of this part with this keyword, but you can not just copy and paste the geometry because gaussian do not understand the code 0 or -1. So you have to copy the geometry, but after that to erase the line where the atom is marked as -1 and so change the nature of the atom which is in the border of the real/model molecule.
Step to calculations with a smaller ring
Back to ONIOM for excited states
Back to ONIOM for crossings
Back to ONIOM
