Ev316
Inorganic Computational Lab
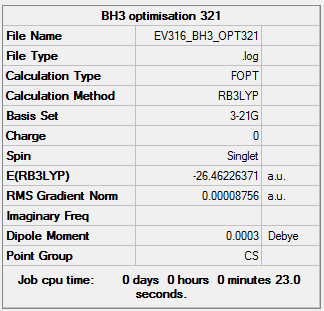
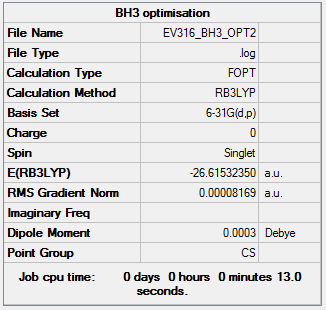
BH3
B3LYP/3-21G level
Item Value Threshold Converged? Maximum Force 0.000217 0.000450 YES RMS Force 0.000105 0.000300 YES Maximum Displacement 0.000692 0.001800 YES RMS Displacement 0.000441 0.001200 YES
The optimisation file is linked to here
B3LYP/6-31G level
Item Value Threshold Converged? Maximum Force 0.000203 0.000450 YES RMS Force 0.000098 0.000300 YES Maximum Displacement 0.000736 0.001800 YES RMS Displacement 0.000394 0.001200 YES
The optimisation file is linked to here
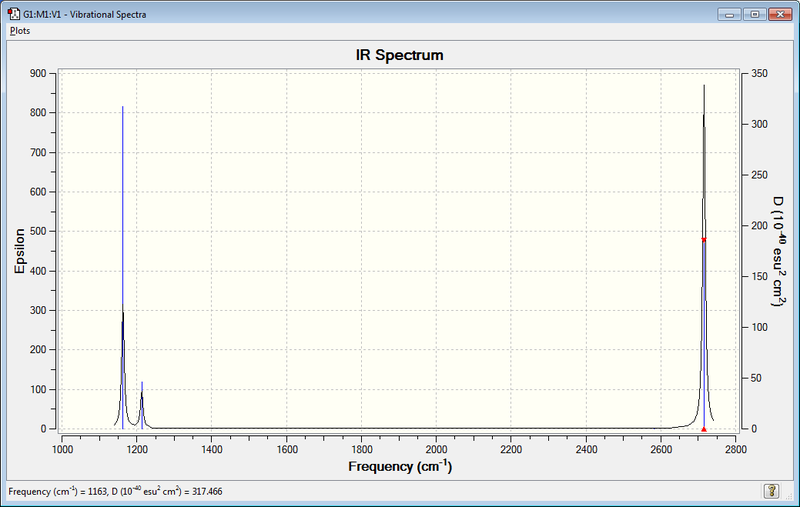
BH3 frequency analysis
The frequency file is linked to here
BH3 B3LYP/3-21G level |
Low frequencies --- -0.2263 -0.1037 -0.0055 47.9770 49.0378 49.0383 Low frequencies --- 1163.7209 1213.6704 1213.6731
IR spectrum
| Mode | Frequency (cm-1 | Intensity | Vibration Type | IR active |
|---|---|---|---|---|
| 1 | 1163 | 92 | Bend, out of plane | Yes |
| 2 | 1214 | 14 | Bend | Yes |
| 3 | 1214 | 14 | Bend | Yes |
| 4 | 2580 | 0 | Symmetric Stretch | No |
| 5 | 2713 | 126 | Asymmetric stretch | Yes |
| 6 | 2713 | 126 | Asymmetric stretch | Yes |
There are less than 6 peaks in the spectrum due to the degeneracy of some vibrations. The second and third, and also the fifth and sixth, vibrations are degenerate. Thus only two peaks are seen as opposed to four. The other vibrational mode that shows no peak is the symmetric stretch, as this gives no change in dipole moment and thus is not IR active it is not seen on the spectrum.
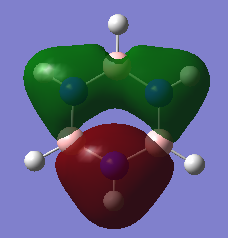
MO analysis of BH3
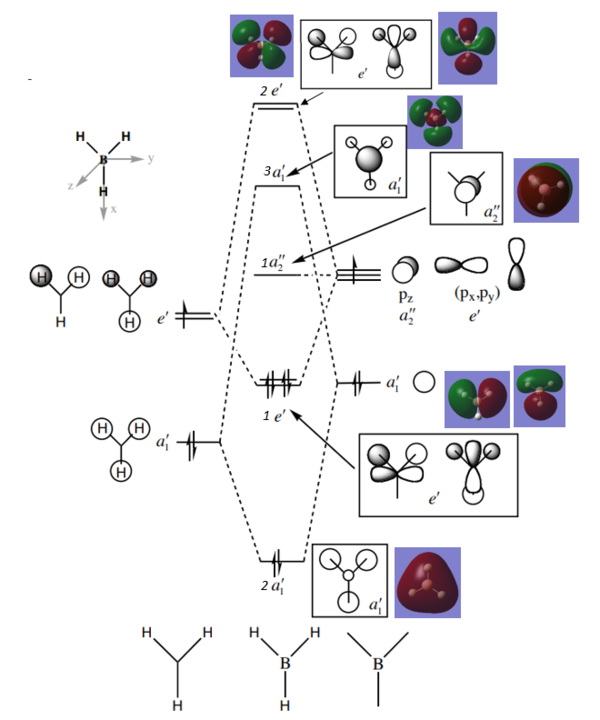
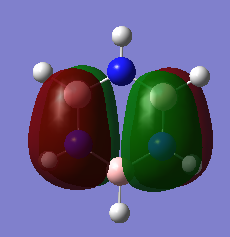
Are there any significant differences between the real and LCAO MOs?
The LCAOs are ordered according to their energy but there is no quantitative analysis of energy as there is with the computed MOs. The real MOs are shown as with complete lobes as opposed to the fragmented LCAO MOs. The overall shape and structure seems to be a good match, yet the size of the lobes is somewhat larger for the real MOs.
Ng611 (talk) 16:21, 29 May 2018 (BST) The absolute size of the lobes isn't something that qualitative MO theory is even able to determine. Instead, what about the relative sizes of the lobes for different atoms? What does this tell you about the utility of MO theory in determining orbital sizes?
What does this say about the accuracy and usefulness of qualitative MO theory?
Qualitative MO theory gives a good insight into the predicted bonding, shape and energy ordering of orbitals, yet does not provide the same level of information as the computed MOs. Qualitative MO theory remains a useful tool for analysis when computational methods are not possible or too expensive.
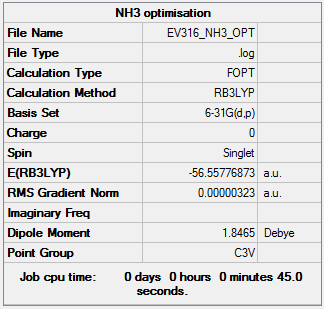
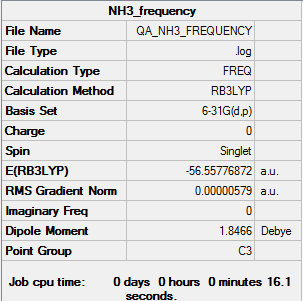
NH3
Using B3LYP/6-31G level
Optimisation
The optimisation file is linked to here
Item Value Threshold Converged? Maximum Force 0.000006 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000012 0.001800 YES RMS Displacement 0.000008 0.001200 YES
Frequency
The frequency file is linked to here
Low frequencies --- -8.5646 -8.5588 -0.0047 0.0454 0.1784 26.4183 Low frequencies --- 1089.7603 1694.1865 1694.1865
Item Value Threshold Converged? Maximum Force 0.000013 0.000450 YES RMS Force 0.000006 0.000300 YES Maximum Displacement 0.000039 0.001800 YES RMS Displacement 0.000013 0.001200 YES
NH3 B3LYP/6-31G level |
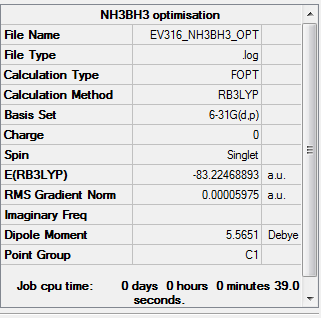
NH3BH3 analysis
Using B3LYP/6-31G level
Optimisation
Item Value Threshold Converged? Maximum Force 0.000122 0.000450 YES RMS Force 0.000058 0.000300 YES Maximum Displacement 0.000513 0.001800 YES RMS Displacement 0.000296 0.001200 YES
The optimisation file is linked to here
Association energy
E(NH3)= -56.55777 a.u. E(BH3)= -26.61532 a.u. E(NH3BH3)= -83.22469 a.u. ΔE=E(NH3BH3)-[E(NH3)+E(BH3)] = -0.0516 a.u. = -135 kJ/mol
The B-N dative bond is weak in comparison to many other covalent bonds. It is weaker than the B-B bond (293 kJ/mol) and the N-N bond (167 kJ/mol) [2]. The calculated value is in the same order of magnitude as other single bond energies, and as such can be considered a reasonable value.
Ng611 (talk) 16:22, 29 May 2018 (BST) Good calculation. Try not to use a website as a reference though.
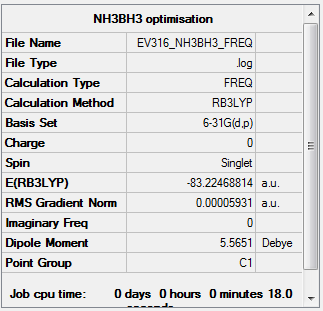
Frequency
Low frequencies --- -12.2585 0.0011 0.0011 0.0012 19.3973 43.3115 Low frequencies --- 266.3451 632.1223 638.3345
Item Value Threshold Converged? Maximum Force 0.000113 0.000450 YES RMS Force 0.000059 0.000300 YES Maximum Displacement 0.000701 0.001800 YES RMS Displacement 0.000347 0.001200 YES
The frequency file is linked to here
Benzene B3LYP/6-31G level |
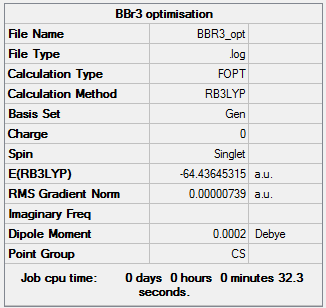
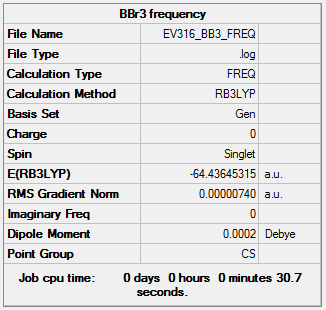
BBr3 analysis
Using B3LYP/GEN level
Ng611 (talk) 16:26, 29 May 2018 (BST) Do you mean LANL2DZ/6-31G? The -gen tag is not a valid basis set descriptor.
Optimisation
The optimisation file is linked to here
Item Value Threshold Converged? Maximum Force 0.000018 0.000450 YES RMS Force 0.000011 0.000300 YES Maximum Displacement 0.000122 0.001800 YES RMS Displacement 0.000075 0.001200 YES
Frequency
The frequency file is linked to here
Item Value Threshold Converged? Maximum Force 0.000019 0.000450 YES RMS Force 0.000007 0.000300 YES Maximum Displacement 0.000145 0.001800 YES RMS Displacement 0.000064 0.001200 YES
Low frequencies --- -0.0002 -0.0001 0.0000 1.7959 3.5786 4.1660 Low frequencies --- 155.9323 156.0231 267.7073
BBr3 B3LYP/GEN |
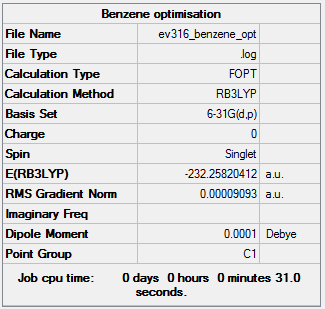
Benzene
Using B3LYP/6-31G level
Optimisation
Item Value Threshold Converged? Maximum Force 0.000198 0.000450 YES RMS Force 0.000082 0.000300 YES Maximum Displacement 0.000849 0.001800 YES RMS Displacement 0.000305 0.001200 YES
The optimisation file is linked to here
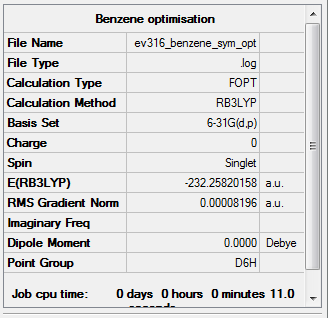
Symmetry
D6h point group was imposed on benzene.
Item Value Threshold Converged? Maximum Force 0.000193 0.000450 YES RMS Force 0.000079 0.000300 YES Maximum Displacement 0.000830 0.001800 YES RMS Displacement 0.000294 0.001200 YES
The symmetry file is linked to here
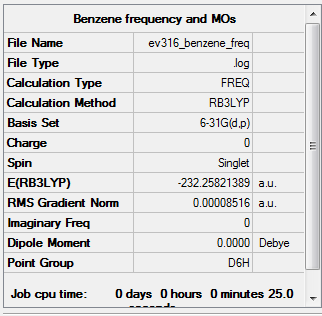
Frequency
Item Value Threshold Converged? Maximum Force 0.000197 0.000450 YES RMS Force 0.000085 0.000300 YES Maximum Displacement 0.000780 0.001800 YES RMS Displacement 0.000333 0.001200 YES
Low frequencies --- -3.5606 -3.5606 -0.0088 -0.0044 -0.0042 10.0905 Low frequencies --- 413.9582 413.9582 621.1416
The frequency file is linked to here
Benzene B3LYP/6-31G level |
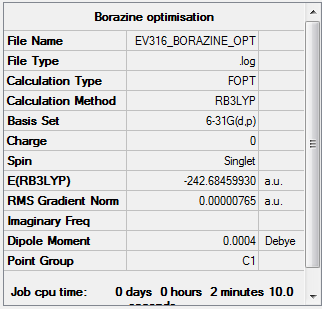
Borazine
Using B3LYP/6-31G level
Optimisation
Item Value Threshold Converged? Maximum Force 0.000021 0.000450 YES RMS Force 0.000006 0.000300 YES Maximum Displacement 0.000142 0.001800 YES RMS Displacement 0.000051 0.001200 YES
The optimisation file is linked to here
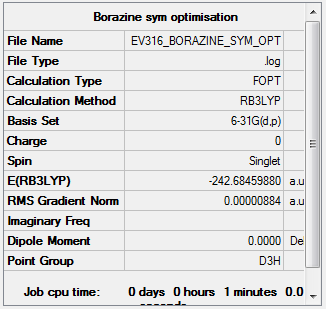
Symmetry
D3h point group was imposed on borazine.
Item Value Threshold Converged? Maximum Force 0.000024 0.000450 YES RMS Force 0.000008 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000031 0.001200 YES
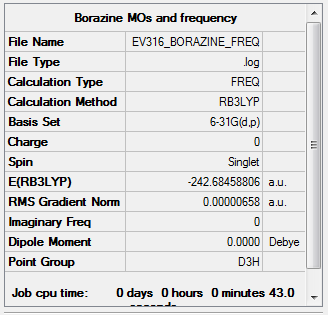
Frequency
Item Value Threshold Converged? Maximum Force 0.000019 0.000450 YES RMS Force 0.000007 0.000300 YES Maximum Displacement 0.000086 0.001800 YES RMS Displacement 0.000033 0.001200 YES
Low frequencies --- -9.6132 -9.3061 -9.0640 -0.0103 -0.0088 0.1106 Low frequencies --- 289.1848 289.1935 403.8445
The frequency file is linked to here
Borazine B3LYP/6-31G level |
Charge Analysis of Benzene and Borazine
The table below details the charge analysis for the two compounds:
Molecule Charge on H Charge on ring atom
Benzene 0.239 -0.239 (C)
Borazine 0.432 (bonded to N) -1.102 (N)
-0.077 (bonded to B) 0.747 (B)
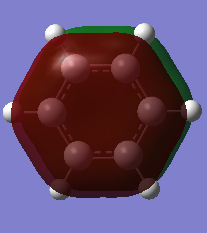
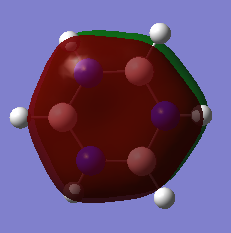
A colour range from -1.102 to 1.102 was used for the NBO charge analysis on both benzene and borazine. Both molecules show a range of charges on the atoms.
In benzene, each carbon atom and each hydrogen atom is equivalent, with identical electronegativities. Therefore, the charge distributions of equivalent atoms is the same. As carbon is more electronegative than hydrogen (2.55 compared to 2.20)[3], it has a negative charge which is equal and opposite to the charge on the H atoms.
Nitrogen (3.04)[4] is more electronegative than hydrogen, whereas boron (2.04)[5] is more electropositive. The nitrogen atoms in borazine are all equivalent and the same can be said for the boron atoms. They all show the same charge, with the charge on B being positive whilst that on N is negative. Unlike in benzene, the charge on the hydrogen atoms differs and depends on the atom to which they are bonded. For those H atoms bonded to B, as they are more electronegative than B, they are hydridic - negatively charged. In comparison, the H atoms bonded to N are protic as hydrogen is more electronegative than nitrogen and thus nitrogen withdraws electron density.
The image below shows the charge analysis for the two compounds:
Ng611 (talk) 16:23, 29 May 2018 (BST) Good discussion of the effects of electronegativity on the overall charge distribution. What do the partial charges sum to, and is there any difference in partial charge for atoms related by symmetry?
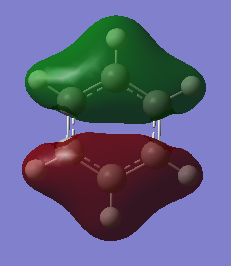
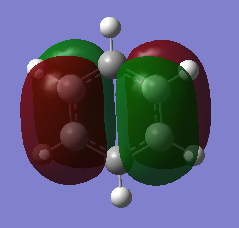
MO Comparison
Isoelectronic benzene and borazine. For both, core molecular orbitals are 1-6.
MO 21 is the HOMO.
MO 22 is the LUMO.
Comparison of MO 9, 17 and 20:
| MO | Benzene | Borazine | Comparison |
|---|---|---|---|
| 9 | 
|
|
The benzene molecular orbital has symmetrical elements (has planes of symmetry), with two out of phase lobes and a centra nodal plane. There is an equal contribution from each C-H bond. The symmetry of the borazine molecular orbital is analogous to that seen in another molecule with the same D3h symmetry (3H e' fragment orbital in BH<sub3 analysis). The benzene lobes are symmetric, whereas the borazine lobes are different shapes to each other. There is no contribution from the H atoms bonded to boron. Nitrogen contributes more bonding character. In the molecular orbitals of both molecules, there is one node which gives some antibonding character, however both molecular orbitals show a greater bonding character, making them bonding overall. The contribution is from s orbitals. Through space out-of-phase interactions of the two lobes is overridden by the sigma bonding character. |
| 17 | 
|
|
This is a bonding molecular orbital, with contributions from the pz orbitals on each C or B/N atom. The shape of the benzene molecular orbital is symmetric, with equal contribution from all C atoms. In borazine, the orbital is not as regular as that in benzene due to the smaller contribution from B, due to it being more electropositive than N. The interactions are pi-type, and this orbital is the one typically pictured for aromatic rings as it shows the contiguous p orbitals. |
| 20 | 
|
|
This molecular orbital shows p-orbital contributions. The overlap of the in phase pz orbitals of 4 of the ring atoms. There is no contribution from 2 of the ring atoms in each complex. The shape of the orbitals is similar for both benzene and borazine. However, the contribution from N is greater than that from B in the borazine molecule, whereas in benzene, the orbitals have an equal contribution from all C atoms. This leads to a distortion of the lobes in borazine, with the lobe being larger on N than on B. There is one central node, which gives the orbital some antibonding character. The through space interaction of the two lobes which are out-of-phase with each other also contributes antibonding character. There is both antibonding and bonding character to this molecular orbital. The through space antibonding character is a weaker interaction than the bonding orbital overlap of the in phase pz orbitals, and thus the overall character of this orbital is likely to be weakly bonding, with pi-type interactions. |
Aromaticity
The empirical rules for aromaticity state that compounds which follow Huckel's rule will be aromatic. For compounds which are planar & have a contiguous, cyclic array of p-orbitals perpendicular to the plane of the ring, the rule states that those with 4n+2 p electrons display special stabilisation[6].
Aromatic stabilisation was originally attributed to the overlap of pz orbitals (as seen in MO17 in the above section) in plane creating a delocalised pi system. This description has since been questioned, as there are many notable exceptions to the rule[7]. There has been some debate over the importance of sigma-electron structure.
The ease of destruction of the planarity of aromatic compounds[8], along with the existence of non-planar compounds with distorted rings but 'aromatic' bond lengths[9], such as para- and meta-cyclophanes, indicate that planarity is not essential for aromaticity. The term aromaticity has been applied to non-traditional molecules such as spherical fullerenes[10].
These exceptions having been studied, the traditional view of aromaticity is being questioned. MO theory and computational methods can be used to investigate the molecular orbitals and explain the stability of aromatic compounds which cannot be explained by the empirical rules. The visualisation of how electrons are delocalised in molecular orbitals across the molecule (as opposed to being contained in bonds) will help in the understanding of aromaticity.
Ng611 (talk) 16:28, 29 May 2018 (BST) Framework for a good dsicussion here -- I'd expand on the points you made a little further and perhaps add some additional discussion regarding experimental techniques and how they can be used to determine aromaticity.
References
Ng611 (talk) 16:29, 29 May 2018 (BST) A few issues here and there (see my notes throughout) but overall a good report. Remember to proofread your work and take care with your formatting.
- ↑ http://www.huntresearchgroup.org.uk/teaching/teaching_comp_lab_year2a/Tut_MO_diagram_BH3.pdf
- ↑ http://www.wiredchemist.com/chemistry/data/bond_energies_lengths.html
- ↑ http://periodictable.com/Properties/A/Electronegativity.al.html
- ↑ http://periodictable.com/Properties/A/Electronegativity.al.html
- ↑ http://periodictable.com/Properties/A/Electronegativity.al.html
- ↑ https://www.imperial.ac.uk/media/imperial-college/research-centres-and-groups/spivey-group/teaching/org1aromatics/lecture11617.pdf
- ↑ Palusiak, M. and Krygowski, T.M., 2007. Application of AIM Parameters at Ring Critical Points for Estimation of π‐Electron Delocalization in Six‐Membered Aromatic and Quasi‐Aromatic Rings. Chemistry-A European Journal, 13(28), pp.7996-8006.
- ↑ Anet, F.A. and Yavari, I., 1978. Force-field calculations for some unsaturated cyclic hydrocarbons. Tetrahedron, 34(19), pp.2879-2886.
- ↑ Jenneskens, L.W., Klamer, J.C., de Boer, H.J., de Wolf, W.H., Bickelhaupt, F. and Stam, C.H., 1984. Molecular Structure of 8, 11‐Dichloro [5] metacyclophane: A Strongly Bent Benzene Ring. Angewandte Chemie International Edition in English, 23(3), pp.238-239.
- ↑ Williams, R.V., 2001. Homoaromaticity. Chemical reviews, 101(5), pp.1185-1204.