Eleonora Physical comp labs
H H H example
1.What value do the different components of the gradient of the potential energy surface have at a minimum and at a transition structure? Briefly explain how minima and transition structures can be distinguished using the curvature of the potential energy surface.
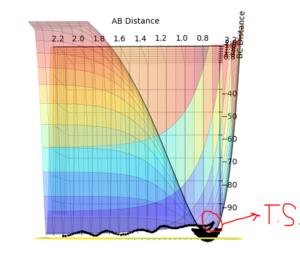
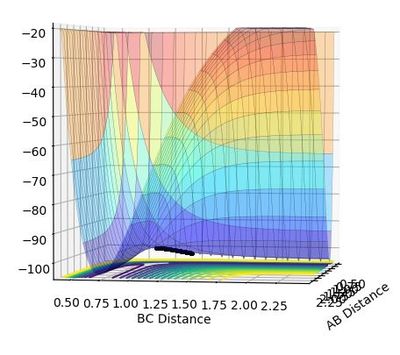
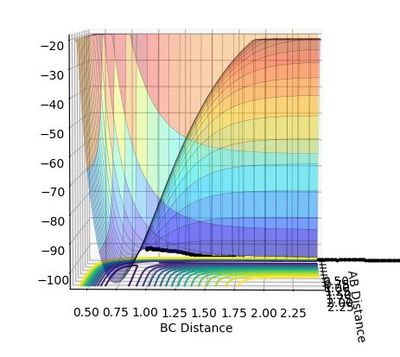
The transition structure is a maximum in the minimum, and can be viewed as such in the surface plot. When differentiated, both the minimum and the transition structure both give zero, but when differentiated again, the transition structure gives a negative value (due to it being a maxima) and the minimum gives a positive value (due to it being the minimum).
Ng611 (talk) 23:38, 7 June 2018 (BST) Good MS paint skills! :) A top-down diagram demonstrating the orthogonal co-ordinates along which the gradients are evaluated would demonstrate your point a bit more clearly though!
2.Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” plot for a relevant trajectory.
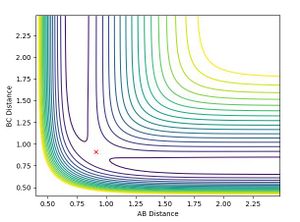
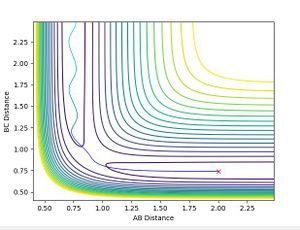
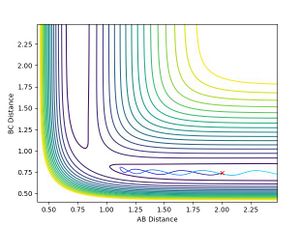
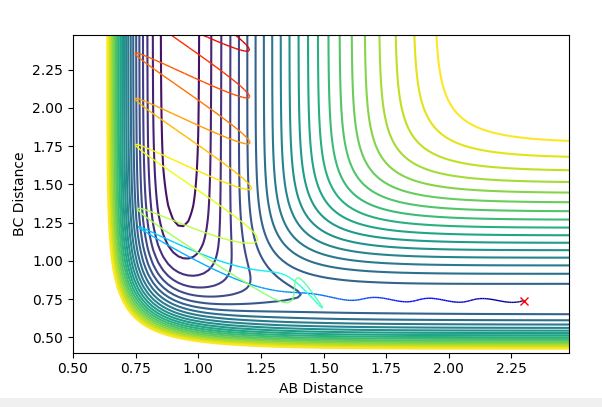
To two decimal places, the transition state positions for the two AB and BC are 0.91 angstrom (A). This is because on the contour plot, the trajectory is non-existent. As this is the transition state, one would expect as such, due to their being no momentum since there is no kinetic energy at the maximum.
This is supported by the internuclear distances vs time plot, which shows that the AB and BC distances are the same, which is what you should see at a transition state. They both oscillate but in phase.
Ng611 (talk) 23:40, 7 June 2018 (BST) Good! The oscillations show that you're a little way off from the true TS, but not by much. You could've run an MEP calculation to find the true TS. Regardless, your estimate is close enough!
3.Comment on how the mep and the trajectory you just calculated differ.
The main difference between these two graphs is the velocity. In the first graph (MEP), the velocity is set to zero at each step, which is why it stops after the line/transition state trajectory reaches a minima. In the case of the dynamic graph, the trajectory continues on to infinity. Both these graphs show that if an infinitesimally small change is made in order to favour the product, then the transition state will 'fall' towards to products, trajectorially speaking and energetically speaking.
4.Complete the table by adding a column with the total energy, and another column reporting if the trajectory is reactive or unreactive. For each set of initial conditions, provide a plot of the trajectory and a small description for what happens along the trajectory.
5.State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?
1. The separation of electronic and nuclear motions occur, equivalent to the Born-Oppenheimer approximation.
2. The reactant molecules are distributed among their states in accordance with the Maxwell-Boltzmann distribution
3. Molecular systems that have crossed the transition state in the direction of products cannot turn around and reform reactants
4. In the transition state, motion along the reaction coordinate may be separated from the other motions and treated classically as a translation. There is the assumption that if the atoms or molecules don't collide with enough energy for the transition structure to be formed, then the reaction will not take place. This is the classical point of view because from a quantum mechanical point of view, tunneling can take place (with a finite possibility). This would mean in physical terms that the particles have a possibility of reacting without colliding with enough energy to overcome the energy barrier. Tunneling is a negligible effect for reactions with large activation energies, but becomes important for low energy barriers.
5. Even in the absence of an equilibrium between reactant and product molecules, the transition states that are becoming products are distributed among their states according to the Maxwell-Boltzmann laws.
(Ok, but most certainly your are quoting these from some reference, which should be cited and acknowledged. João (talk) 19:31, 15 May 2018 (BST))
Transition state theory underestimates the rate of the reaction. There are two assumptions that have been made which go against what is viewed in the graphs above. The first discrepancy is the "Molecular systems that have crossed the transition state in the direction of products cannot turn around and reform reactants". As can be seen in the contour plot, the molecule will reach a transition state position, then either proceed onward to the products, or go back down to the reactants. This shows that even if the transition state is achieved, the products won't necessarily be formed. The second assumption which is an issue is that "in the transition state, motion along the reaction coordinate may be separated from the other motions and treated classically as a translation". As can be viewed in the surface plot, the transition state is rather low in energy, and so there is a low energy barrier. In these cases, the low energy barrier means that the quantity of tunneling that occurs is greater and therefore significant. Ignoring this means that the rate of reaction predicted by the transition state theory will be significantly lower than what it actually is.
F H H example
6.Classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?
The F + H2 -> H + HF is an exothermic reaction. This can be seen with the graphs as the products are lower in energy than the reactants. The HF bond energy is higher than the H2 bond and so overall energy is released, making the reaction exothermic, thus proving the graph is correct. (H-F 565 pm)
In the case of HF + H -> H2 + F the reaction is endothermic - seen by the fact that the products are higher in energy than the reactions. This also explains why the reaction is not feasible; the HF bond requires too much energy to be broken. (H-H 432 pm)
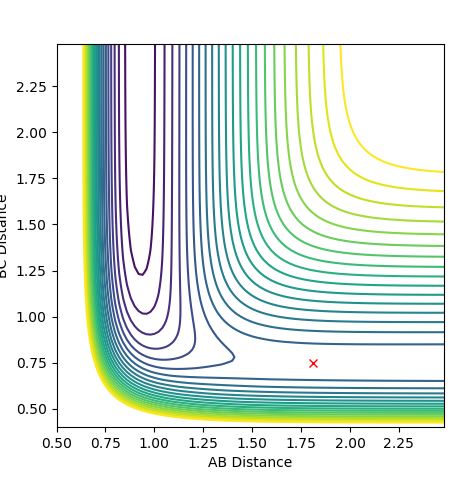
7.Locate the approximate position of the transition state.
H-F bond distance = 1.81 A
H-H distance = 0.746 A
The graph below confirms this since there is only one point and no trajectory.
8. Report the activation energy for both reactions.
H-H formation activation energy
The activation energy for the formation of H2 is:
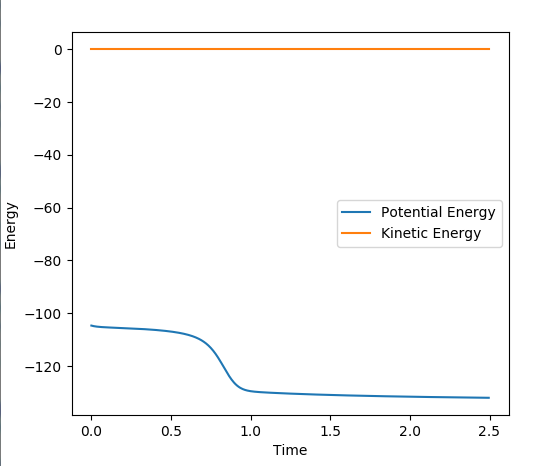
-105.21-(-130.951) = 25.741 kcal/mol. In the graph the potential energy has two plateaus, one of which is higher than the other. The higher energy shoulder is when the transition state is existing, then energy is lost when the transition state goes down to the product.
Ng611 (talk) 23:42, 7 June 2018 (BST) This estimate is a little on the low side. Why might this be?
H-F formation activation energy
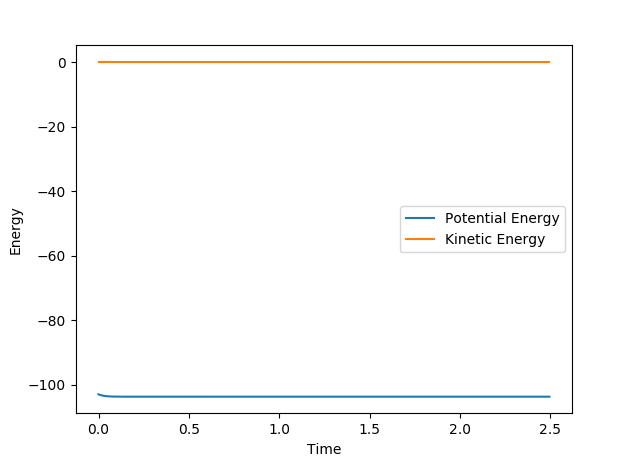
The activation energy for the formation of HF is: -103.015-(-103.708) = 0.693kcal/mol. In the graph the potential energy appears to be flat, but when magnified, there is a very small shoulder at the beginning of the line, which has a small difference of 0.693kcal/mol. The difference is so small due to the formation of HF being so easy.
9.In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. How could this be confirmed experimentally?
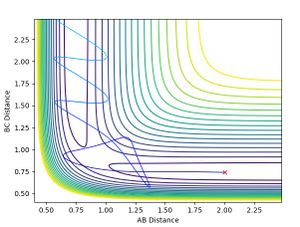
Upon viewing the contour plot of a successful reaction in the formation of HF, it can be seen that the initial trajectory of the reactants has very little oscillation due to the starting material having almost only potential energy. Once the transition state is surpassed however, the oscillations increase in magnitude and this is due to the energy being converted to kinetic energy.
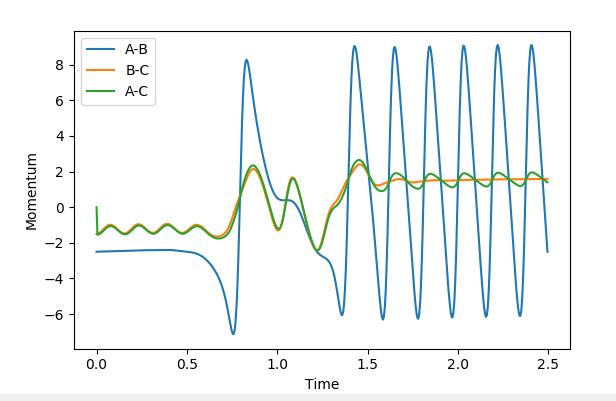
This in turn is backed by the momenta graphs. By the end of the reaction, the BC momentum is the potential energy and the AB momentum is the vibrational energy. At the beginning the AB bond has a constant momentum (due to it being purely potential), then, when it's beyond the transition state there is very large oscillation due to the kinetic contribution. The inverse can be seen for the BC bond as it starts with a small amount of kinetic energy, then once it has surpassed the transition state the momentum plateaus so the momentum becomes purely potential.
This can be measured experimentally due to kinetic oscillations releasing a large amount of heat.
Ng611 (talk) 23:43, 7 June 2018 (BST) True, but enhance translational energy will also manifest as heat. How could you distinguish between the two?
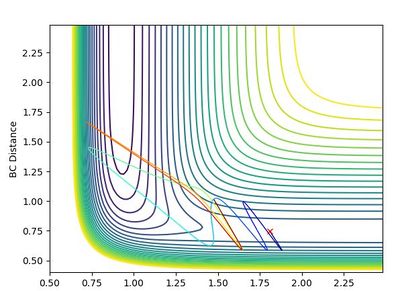
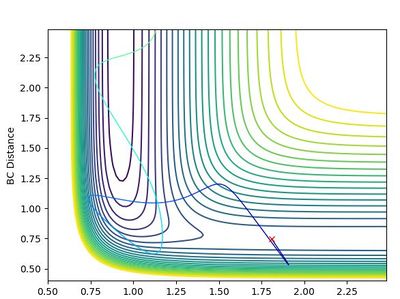
10. Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.
The Polanyi rules state that the vibrational energy is more efficient in promoting a later-barrier reaction than translational energy. This is relevant due to the position of the transition state. When looking at the potential energy surface of the formation of HF, the transition state position is early. This means that when talking about the energies in question, an increase in vibrational energy of the bond will not favour an increase in the rate of the reaction. This can be proven by altering the momentum of the AB and BC bonds.
In the forward reaction of the formation of HF, the AB momentum (translational momentum) was set at a minimal value (-0.5kg.m/s) and the BC momentum (vibrational momentum) was set at -4kg.m/s and -5.5kg.m/s. At -4kg.m/s the reaction was not feasible whereas at -5.5kg.m/s it is. This shows how, due to the transition position being so early, the translational energy being so low has no effect on the feasibility of the reaction. The vibrational energy has to be higher because of this.
Ng611 (talk) 23:48, 7 June 2018 (BST) This is actually the opposite of what is happening. A vibrational energy of -5.5 kg/ms-1 is quite large, especially for such a low activation barrier. By reducing the vibrational energy and increasing the translational, you could make the reaction go with far less momentum.
In the backward reaction of the formation of HF, the AB momentum (still translational momentum) was again kept constant again at -0.5kg.m/s and the BC momentum (vibrational momentum) was altered. In this case of the formation of H2, the transition state is late, and this suggests that this vibrational energy greatly affects the efficiency of the reaction. Since in this reaction only -2.9 kg.m/s, this shows that Polanyi's rule applies and is correct.
Ng611 (talk) 23:50, 7 June 2018 (BST) What about a trajectory that makes the reverse reaction go? Is there one?
Ng611 (talk) 23:50, 7 June 2018 (BST) This was a good report in many places, although quite a few of your explanations -- particularly in this last section -- seemed a bit confused. Remember also to cite any sources you consulted when writing this report; the fact that it's a wiki doesn't exempt you from referencing.