Ef108M1:Imp3rial
Written by Enrico Fantoni
Module 1 - Computational Chemistry Laboratory, Year 3
The hydrogenaton of cyclopentadienyl dimer
The dimerisation reaction of cyclopentadienyl leads to the selective formation of the endo dimer, as opposed to the exo dimer.
When seeking the reason why this is, in molecular mechanical terms, one discovers that the lowest energy conformation is the exo one, 31.8834 kcal/mol, against a higher, 34.0145 kcal/mol, energy of the endo form.
From this one can conclude that the selectivity is due to a kinetic control of the reaction. The product which has the lowest activation energy requirements will be favoured and will win over the formation of the other product. This feature will overcome the higher thermodynamical stability and, hence, lower energy, of the exo dimer.
For what concerns the hydrogenation, instead, one can deduce from thermodynamic data that the more favoured product is that which retains the olefin furthest away from the bridgehead structure. The data is reported here-below.
| species 3, hydrgenated in 5-membered ring (kcal/mol) |
species 4, hydrogenated close to bridgehead structure (kcal/mol) | |
|---|---|---|
| stretch | 1.3035 | 1.1146 |
| bend | 19.8181 | 14.4867 |
| torsion | 10.8217 | 12.5058 |
| 1,4 VdW | 5.6313 | 4.5021 |
| non 1,4 VdW | -1.1995 | -1.0270 |
| Stretch - Bend | -0.8382 | -0.5497 |
| Dipole/dipole | 0.1620 | 0.1407 |
| Total energy | 35.6989 | 31.1732 |
The data above shows that while species 4 can bend more freely and is subject to less VdW forces, species 3 has an easier torsion. Stretching energies are very similar. No H-bonding exists for this molecule. Overall, species 4 is lower in energy, hence more stable.
Also, no great difference can be noticed between the stretch-bond energies, the non-1,4 VDW energies and the dipole/dipole energies of the two species.
So why is species 4 more energetically stable? Probably it has to do with a lower steric clash, as a higher electron density further away from the bridgehead structure is more likely to lead to a lower energy molecule. The easier torsion of the 5-membered ring on species 3 doesn't have the same impact as the ability of 4 to bend more freely.
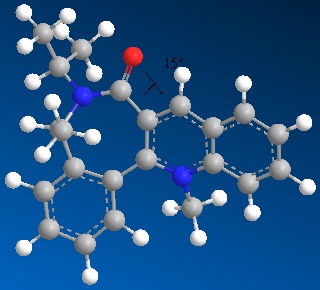
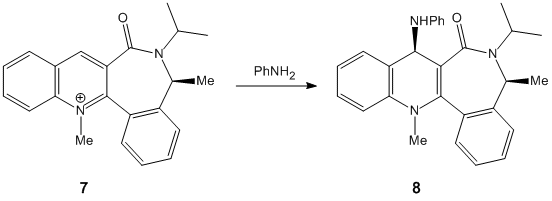
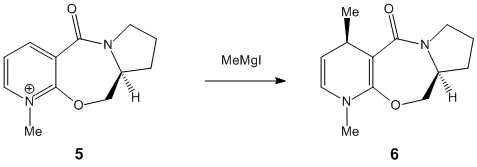
Stereochemistry of nucleophilic additions to a pyridinium ring (NAD+ analogue)
The two molecules 5 and 7 display an interesting dihedral angle between the carbonyl oxygen and the plane of the pyridinium rings of 12° for species 5 and of 15° for species 7, as shown. This fact is very important to explain the stereocontrol seen in 5 and 7 (the added groups are cis to the carbonyl rather than anti).
In 5, the dihedral angle has an effect on the stereochemistry due to the coordination between the Grignard reagent and the amide oxygen atom [1].
Hence, conjugate delivery of the methyl from Mg to C(4) of the carbonyl results in an addition of the methyl "cis" to the carbonyl and the temporary generation of a magnesium enolate (relative energy 43.1149 kcal/mol).
In 7, stereoselectivity is due to similar reasons: a steric control exerted by the carbonyl sitting on the lactam[2] (relative energy of 80.4292 kcal/mol).
| Species 7 | Species 5,6,7&8 |
|---|---|
 |
|
Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol
Taxol is an atropisomeric molecule that can have the carbonyl group facing either up or down.
The most stable isomer appears to be species 10, the one with the carbonyl facing down, by a very slight energetic difference. This species is less strained and Being atropisomers, 9 and 10 can interconvert if sufficient energy is given to the system to overcome the TS energy barrier. The slight higher stability of 10 arises after MMFF94 minimisation. (Relative energy of 9: 54.3439 kcal/mol vs. energy of 10: 53.1427 kcal/mol).[3] Further analysis of the split energies reveals a slight higher bending and van der Waals stability of the "down" conformer, which leads one to think that the VdW distance between the hydrogens on the "upper" part of the molecule interact favourably due to a more natural bending of the molecule (see image on the right).
| species 10, carbonyl down | species 9, carbonyl up |
|---|---|
 |

|
Then why does the alkene react so slowly?
The olefin is hyperstable hence it reacts slowly. Meier and Schleyer suggest[4] that this is due to a lower degree of strain of the olefin as opposed to that of the corresponding saturated analogue and generally to other olefins. Lower strain brings to a better π overlap: the LUMO is higher and the HOMO is lower in energy. This results in an overall lower reactivity of the so called hyperstable alkene, often present in bridgehead olefins like 10.
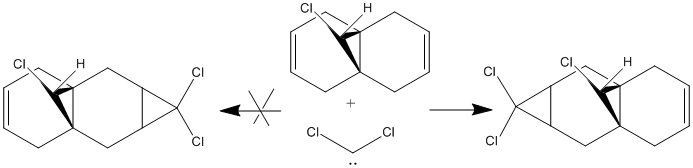
Regioselective addition of dichlorocarbene
Can we predict the reactivity of a molecule via molecular modelling of the molecular orbitals’ shape? , shown on the right
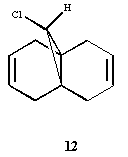
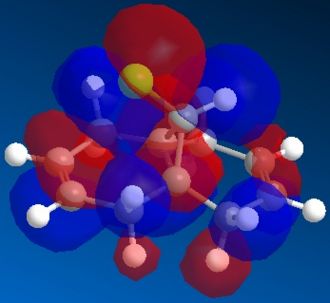
, serves as an example for this purpose. Analysing the orbitals (below) allows one to make a series of considerations on the molecule. In primis, since we are looking for an explanation of the reactivity of the molecule: are both olefins playing the same role? Does one have more electron density than the other (in which case it would act as nucleophile)? The HOMO orbital shows that the syn olefin is most likely responsible for providing the electrons in the reaction between molecule 12 and dichlorocarbene. In fact, it clearly has a π bonding interaction on the syn olefin in the HOMO, which means that it has high electron density on that bond and could act as the nucleophile in the reaction.
Looking closely at the HOMO picture, we can detect (as suggested by Halton et al.[5]) a slight bump in the bonding orbital surrounding the syn alkene towards the antibonding C-Cl interaction. This suggests that the C-Cl σ* orbital (LUMO+1) electrons are participating in the alkene electron cloud, giving more strength to the nucleophilic character of the syn olefin. From an MO point of view, the interaction between the C-Cl bond and the alkene π bond creates a more stable bonding situation (when the C-Cl orbital and the alkene one are in-phase) and a more unstable anti-bonding situation (when the C-Cl orbital and the alkene one are out-of-phase, as in the HOMO). The less stable situation (still electron-full) is hence ideally high in energy to donate nucleophilically.

Moreover, the LUMO, being an unoccupied orbital, is unable to donate electrons. Rather, it could potentially accept electrons in the antibonding π* interaction on the anti alkene, but only if a nuclephilic species with a higher-in-energy orbital was to be donating them. This, though, is not the case in this instance.
Furthermore, if it is true that the syn alkene’s bonding orbital (which creates a stabilising effect to the molecule donates to the dichlorocarbene, we should be able to see a looser C-C bond in the final product, as electrons have been removed from a stabilising orbital. This is in fact the case since the double bond has become a single bond in the product.[6][7]
| HOMO-1 | HOMO | LUMO |
|---|---|---|
 |
 |
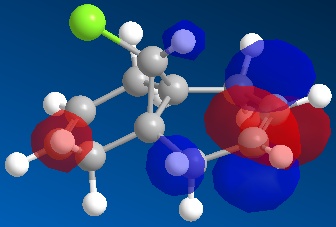 |
| LUMO+1 | LUMO+2 | |
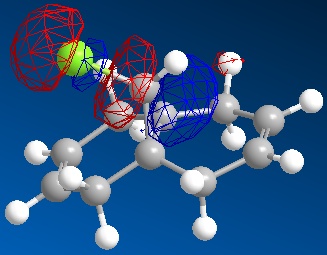 |
 |
| Diene frequencies (cm-1) | Mfrequencies (cm-1) | |
|---|---|---|
| C-Cl stretches | 770.93 901.56 930.14 952.34 1040.00 |
774.99 908.69 925.84 |
| syn olefin | 1736.99 | 1757.32 |
| anti olefin | 1758.07 |
The vibrational frequencies reported above support all that has been said; in the diene, the frequency of vibration of the syn olefin is lower than that of the anti olefin, hence it’s energetically stronger and more stable than the other olefin. In the monoene, the frequency of the syn olefin increases, i.e. the energy of the bond decreases, the bond is looser. The same applies to the σ* orbital of C-Cl. Possibly, in the monoene the overlap of the C-Cl orbital to the π bond is weaker, meaning that the π bond is weaker (lower electron density) and that the σ* orbital has a more radical antibonding effect on C-Cl and weakens it.
Miniproject
In this section, a diastereomeric mixture as product of a reaction is analysed via computational methods. The reaction chosen is:

This directed dihydroxylation of an allylic alcohol has been shown to have high yields[8] and to be stereoselective when catalysed by OsO4. The catalyst can further be re-oxidised by employing NMO. The reaction was reported to give an 85:15 mixture of the cis/trans vs. the all-cis isomer when OsO4, NMO, acetone and H2O are used as catalysts[9]. Other syntheses methods reported in the same publication a higher selectivity for the second compound when using as reagents OsO4 with CH2Cl2 (63:37) or OsO4 (1 mol%) with Me3NO.2H2O (1.3 equiv.), DCM (45:55).
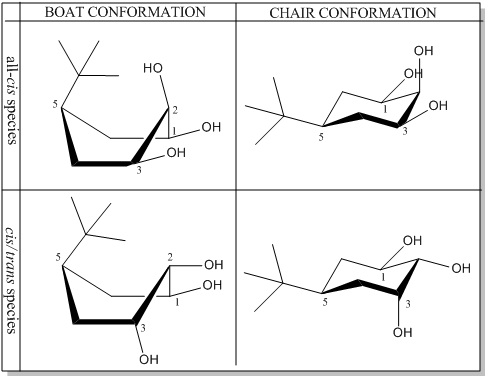
NOTE: For ease of comparison between the two species, the numbering of the atoms in all of the following section will be based on that of the picture below on the LEFT.
| all-cis species | cis/trans species |
|---|---|
 |
 |
Computational analysis of the two isomeric products - that here we'll call all-cis and cis/trans species, respectively - can distinguish diasteromers by different techniques:
- J coupling constants: the cis/trans species should have a larger J coupling value than in the all-cis corresponding case for H20-H21 and H21-H14, as they appear to have an angle of about 90° between each other in the latter. According to the Karplus equation, this angle corresponds to a lower degree of coupling, hence a smaller J value. On the other hand, H20-H18 should be smaller for the cis/trans species, given that the two hydrogens are syn to each other (~90° angle).
- Optical rotation: the isomers will have different OR as the products are chiral and asymmetric. Hence, they will interact with light differently. Unfortunatly, the OR data is not available in the literature for comparison.
- 13C NMR, IR and point group of the molecule do not particularly distinguish the two diasteromers but they do specifically identify the compound.
Miniproject data section
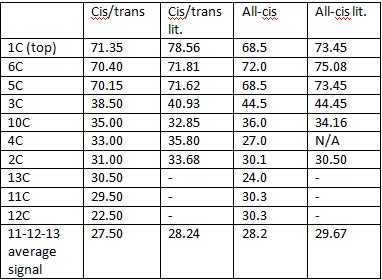
- 13 C NMR data:
Cis/trans computational
δ(50 MHz,TMS) 71.35 (CH, C-1), 70.40 (CH, C-6), 70.15 (CH, C-5), 38.50 (CH, C-3), 35.00 (C, C-10), 33.00 (CH2, C-4), 31.00 (CH2, C-2), 27.50 (CH3, C-11-12-13);
Cis/trans literature
δ(50 MHz, CD3OD) 78.56 (CH, C-1), 71.81 (CH, C-6), 71.62 (CH, C-5), 40.93 (CH, C-3), 35.80 (C, C-4), 33.68 (CH2, C-2), 32.85 (CH2, C-10), 28.24 (CH3, C-11-12-13);
All cis computational
δ(50 MHz, TMS) 72.0 (CH, C-6), 68.5 (2 × CH, C-1 and C-5), 44.5 (CH, C-3), 36.0 [C, C(CH3) 3], 30.1 (CH2, C-4), 30.1 (CH2, C-2), 29.67 (CH3);
Cis/trans literature
δ(50 MHz, D2O) 75.08 (CH, C-6), 73.45 (2 × CH, C-1 and C-5), 44.45 (CH, C-3), 34.16 [C, C(CH3) 3], 30.50 (CH2, C-2), 29.67 (CH3).
Literature values are taken from [9].
All the data for the cis/trans molecule has similar ppms to the all-cis one. Hence, it is not much useful to distinguish between the two isomers, but it can identify the compound quite precisely. If we take into account the different conditions of measurement, the computational NMR values and the literature values are within a very close range of each other, hence they are very reliable to identify the compound.
Note: why are the literature values for 11C, 12C and 13C missing? The rapid tumbling (faster timescale than that on which the NMR is run) of the 3 carbons of the tBu group creates an averaged effect for the the atoms at high temperatures and 1 peak is recorded. In order to achieve the 3 separate values, one would need to cool the molecule and perform an NMR at those low temperature, allowing a lower degree of tumbling and rotation.
| All-cis 13C NMR | Cis/trans 13C NMR |
|---|---|
Click on image to enlarge |
Click on image to enlarge |
- J coupling costants
The coupling constants are the key tool, in this miniproject, to identify the diastereomers.
Cis/trans species J couplings

- There was no match when cross-referencing, probably due to experimental errors. The value reported is rounded to the nearest Hz.
The last two lit. values are identical due to the rapid motion of C4H(up) and C4H(down) in real-life, room temperature NMR. Hence, the values correspond to an average of the two low temperature values.
The data is not matching. The reason for this is that the energy minimisation with Gaussview gave the more unstable boat conformation as opposed to the chair conformation. Hence, the J couplings don’t correspond. As can be seen in the scheme below, changing the conformation of the molecule brings to a major difference in the position of the substituents, varying considerably the coupling constants. (Time constraints don't allow a recalculation of the J couplings.)
All-cis species J couplings

As above, the last two lit. values are identical due to the rapid motion of C4H(up) and C4H(down) in real-life, room temperature NMR. Hence, the values correspond to an average of the two low temperature values. The first two values, instead, are identical as the all-cis chair conformation molecule has σv symmetry and hence belongs to the Cs point group!
- IR spectra
Cis/trans species computational
vmax(gas phase)/cm-1: 3734.67 (OH stretch), 3050 (average CH stretch), 1126.13 (C-O stretch)
Cis/trans species literature
vmax(Nujol)/cm-1: 3343br s (OH stretch), 2859 (CH stretch), 1094 (C-O stretch);
All-cis species computational
vmax(gas phase)/cm-1: 3687.74 (OH stretch), 3040 (average CH stretch)
All-cis species literature
vmax(neat)/cm-1: 3396br s (OH stretch), 2959 and 2868 (CH stretch)
| Cis/trans comp. | Cis/trans lit. | All-cis comp. | All-cis lit. | |
|---|---|---|---|---|
| OH stretch | 3734.67 | 3343br | 3687.74 | 3396br |
| CH stretch | 3050 | 2859 | 3040 | 2959, 2868 |
| COH stretch | 1126.13 | 1094 |
The IR frequencies are higher for the computational data, also when talking into account an 8% shift due to empirical errors. However, the difference is narrow and can still be attributed to the different conditions in which the experimental and the computational data were obtained.
In any case, the two spectra are far too similar to be indicative of any difference between the two diasteromers. However, they do provide a means of identification of the species in question, regardless of its diasteromeric form.
| All-cis IR | Cis/trans IR |
|---|---|
Click on image to enlarge |
Click on image to enlarge |
- Point group: C1 for both species.
In conclusion, the J couplings should suffice to identify the diastereomeric species[10]. However, an error occurred which prevented this direct link to be demonstrated in this report. IR, and NMR are useful to identify the compound, in fact data match between the computational and literature values was a bit more evident in that case, although the different conformation of the molecule might have affected those calculations too. OR data could not be retrieved or found in literature. Other techniques such as Raman spectroscopy [11], X-ray christallography or NOESY.
References
- ↑ A. G. Shultz, L. Flood and J. P. Springer, J. Org. Chemistry, 1986, 51, 838. DOI:10.1021/jo00356a016
- ↑ S. Leleu, C.; Papamicael, F. Marsais, G. Dupas, V.; Levacher, Vincent. Tetrahedron: Asymmetry, 2004, 15, 3919-3928. DOI:10.1016/j.tetasy.2004.11.004
- ↑ "S. W. Elmore and L. Paquette, Tetrahedron Letters, 1991, 319; DOI:10.1016/S0040-4039(00)92617-0 10.1016/S0040-4039(00)92617-0 10.1016/S0040-4039(00)92617-0"
- ↑ W F Maier, PvR Schleyer, J. Am. Chem. Soc., 1981, 103 (8), pp 1891–1900; DOI: 10.1021/ja00398a003
- ↑ B. Halton, R. Boese and H. S. Rzepa., J. Chem. Soc., Perkin Trans 2, 1992, 447. DOI:10.1039/P29920000447
- ↑ H. S. Rzepa, Michael L. Webb, Alexandra M. Z. Slawin and David J. Williams, J. Chem. Soc., Chem. Commun., 1991, 765-768 DOI: 10.1039/C39910000765
- ↑ H. S. Rzepa, W. A,. Wylie, Int. J. of Quant. Chem., 1992, 44, 4, 469-476. DOI: 10.1002/qua.56044040
- ↑ Donohoe, Moore and Beddoes, Tetrahedron Letters, 1997, 38, 28, 5027-5030
- ↑ 9.0 9.1 Donohoe, Moore and Beddoes, J. Chem. Soc., Perkin Trans. 1, 1997
- ↑ K.Schmidt, ARKIVOC, 2008, 8, 68-73
- ↑ Wong, Georgakis, Cryst. Growth Des., 2008, 8, 12, 4398–4408