Danspage

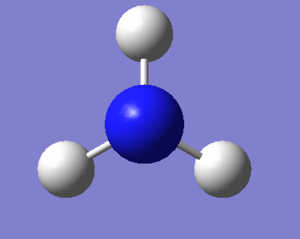
Ammonia NH₃

Figure 1: A Gaussview image of an optimised NH_{3 .}

Parameters from optimisation

Ammonia can be modelled using gaussiview. This model can then be optimised by finding the stable equilibrium arrangement of the atoms. From this optimisation, a series of parameters can be extracted. These parameters are listed in the table below.

Ammonia Data

Query	Result
Molecule	NH3
Calculation method	RB3LYP
Basis Set	6-31G(d,p)
Final Energy (au)	-56.55776873
RMS Gradient (au)	0.00000485
Point group	C3V
N-H Bond length (Å)	1.01798
H-N-H Bond Angle(°)	105.74115

Table 1: Ammonia Data

        Item             Value        Threshold    Converged?
Maximum Force            0.101823     0.000450     NO 
RMS     Force            0.068634     0.000300     NO 
Maximum Displacement     0.187375     0.001800     NO 
RMS     Displacement     0.123109     0.001200     NO 
Predicted change in Energy=-4.704240D-02

Table 2: Ammonia 'item' table

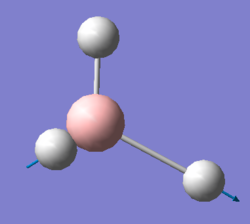
Figure 2:jmol image of optimised Ammonia

The optimisation file is linked to here

Vibrations in Ammonia

Figure 3: Vibrational modes of NH_{3 .}

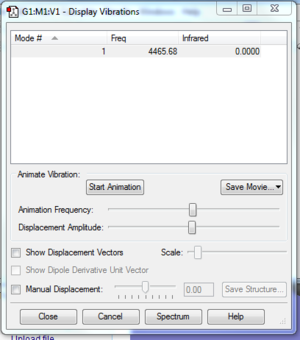
Parameters from molecular vibrations in Ammonia

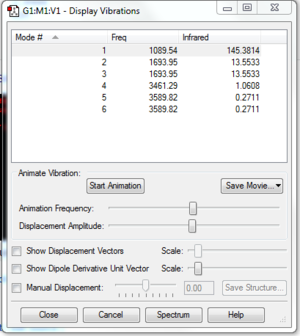
Query	Result
Expected number of nodes	3N-6= 3(4)-6= 6
Degenerate modes	2
Bending modes	3
Stretching modes	3
Highly symmetric mode	Mode 4 (stretching mode)
Umbrella mode	Mode 1 (bending mode)
Expected bands in experimental spectrum	2

Table 3: Questions on vibrational modes in Ammonia

Charge Distribution

Figure 4: Charge Distribution on a Ammonia molecule

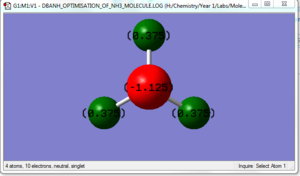
Nitrogen is more electronegative than hydrogen so the expected charge distribution would be a positive dipole on the hydrogen and a negative dipole on the nitrogen. The charge on the Nitrogen atom is -1.125 whilst the charge on the hydrogen atoms is +0.375.

Nitrogen

Figure 4: A Gaussview image of an optimised N_{2 .}

Parameters extracted from optimisation of N₂

Nitrogen Data

Query	Result
Molecule	NH3
Calculation method	RB3LYP
Basis Set	6-31G(d,p)
Final Energy (au)	-109.52412868
RMS Gradient (au)	0.00000060
Point group	D*H

Table 4: Nitrogen Data

 

         Item             Value        Threshold    Converged?
 Maximum Force            0.000001     0.000450     YES
 RMS     Force            0.000001     0.000300     YES
 Maximum Displacement     0.000000     0.001800     YES
 RMS     Displacement     0.000000     0.001200     YES
 Predicted change in Energy=-3.401079D-13

Table 5: Nitrogen item table

Figure 5:jmol image of optimised Nitrogen

The optimisation file is linked to here

Vibrational modes of N₂

Figure 6: Molecular vibrations window for Nitrogen in Gaussview.

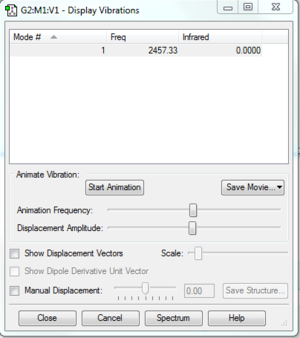
Hydrogen

Figure 7: A Gaussview image of an optimised H_{2 .}

Parameters extracted from optimisation of H₂

Hydrogen Data

Query	Result
Molecule	NH3
Calculation method	RB3LYP
Basis Set	6-31G(d,p)
Final Energy (au)	-1.17853936
RMS Gradient (au)	0.00000017
Point group	D*H

Table 6: Hydrogen Data

         Item             Value        Threshold    Converged?
 Maximum Force            0.168347     0.000450     NO 
 RMS     Force            0.168347     0.000300     NO 
 Maximum Displacement     0.119698     0.001800     NO 
 RMS     Displacement     0.169278     0.001200     NO 
 Predicted change in Energy=-2.130559D-02

Table 7: Hydrogen 'item' table

Figure 8:jmol image of optimised Hydorgen

The optimisation file is linked to here

Vibrational modes of H₂

Figure 9: Molecular vibrations window for Hydrogen in Gaussview.

Haber process

Energies of species in the Haber process

Item	Energy (au)
NH3	-56.55776873
2*NH3	-113.1155375
N2	-109.52412868
H2	-1.17853936
3*H2	-3.53561808
ΔE	-0.05579074

Table 8: Energy change in the Haber process

ΔE for the Haber process is -0.05579074 or -146.479 KJ mol^-1

This overall energy change is negative so the reactants are less thermodnamically stable compared to the products.

Borane

Figure 10: A Gaussview image of an optimised BH_{3 .}

Borane Data

Query	Result
Molecule	BH3
Calculation method	RB3LYP
Basis Set	6-31G(d,p)
Final Energy (au)	-26.61532364
RMS Gradient (au)	0.00000211
Point group	D3H
B-H Bond length (Å)	1.19232
H-B-H Bond angle (°)	120.00000

Table 9: Borane data

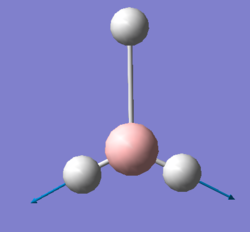
Figure 11:jmol image of optimised Borane

The optimisation file is linked to here

         Item             Value        Threshold    Converged?
 Maximum Force            0.006105     0.000450     NO 
 RMS     Force            0.003997     0.000300     NO 
 Maximum Displacement     0.023278     0.001800     NO 
 RMS     Displacement     0.015239     0.001200     NO 
 Predicted change in Energy=-2.135202D-04

Table 10: Borane 'item' table

Vibrations

Figure 12:Summary of vibrations in Borane

Vibrational modes in Borane

Mode #	Frequency	Infrared	Image
1	1162.97	95.5682	Figure 13: Vibrational mode 1 in Borane
2	1213.14	14.0550	Figure 13: Vibrational mode 2 in Borane
3	1213.14	14.0544	Figure 13: Vibrational mode 3 in Borane
4	2582.58	0.0000	Figure 13: Vibrational mode 4 in Borane
5	2715.72	126.3320	Figure 13: Vibrational mode 5 in Borane
6	2715.72	126.3260	Figure 13: Vibrational mode 6 in Borane

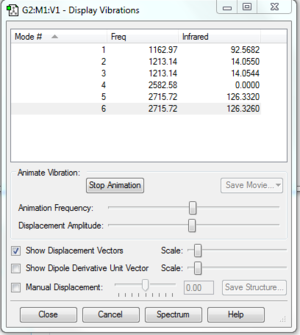
Table 11: Informatin on Vibrational modes in Borane

Borane has 2 sets of degenerate vibrational modes. One vibrational mode doesn't appear in the Infrared spectrum because the stretching vibrational mode doesn't result in a change in dipole moment so cannot be detected by Infrared spectroscopy. The number of vibrational modes is also expected. Borane should have 3N-6 vibrational modes because it is non-linear. This is consistent with the 6 vibrational modes shown in the above table: 3(4)-6= 6.

Charge distribution

Figure 14: Charge distribution on Borane

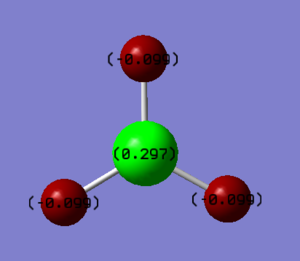
Boron is slightly more electropositive compared to Hydrogen so as a result, negative charge on Borane is skewed towards the hydrogen atoms. This is due to hydrogen atoms being smaller than Boron atoms. However, Borane doesn't have a dipole moment as it has a D3H point group so is arranged with a trigonal planar structure. Due to this symmetry, There is no overall dipole. The Boron has a charge of +0.297 and the hydrogen atoms have a charge of -0.099.

Molecular orbitals

Molecular orbitals in Boron trifluoride are formed by the combination of Atomic orbitals from the Boron atom and Ligand group orbitals (LGOs) formed by the combination of the hydogren atomic orbitals. Combining the Hydrogen atoms forms 3 LGOs. LGO 1 is a bonding molecular orbital formed, LGO 2 is a non bonding molecular orbital and LGO 3 is an anti bonding molecular orbital. These LGOs ten combine with the 2s and 2p orbitals to form new molecular orbitals. The Boron 1s orbital is too deep in energy to participate in the formation of new molecular orbitals.

5 molecular orbitals from Borane

Molecular orbital#	Energy	Bonding/ Anti-bonding	AO/LGO contributions	Image	Description
1	-0.51254	Bonding	2s from the boron and LGO 1	Figure 15: Molecular Orbital 1 Borane	This molecular orbital has no negative phase as it is formed of LGO 1 which is positive in phase for all 3 Hydrogens and a Boron 2s orbital.
2	-0.35079	Bonding	2py from boron and LGO 2	Figure 16: Molecular Orbital 2 Borane	This molecular orbital has an anti phase due to the anti phase chracter of the spy and one of the hydrogens in LGO 2
3	-0.35079	Bonding	2px from Boron and LGO 3	Figure 17: Molecular Orbital 3 Borane	This orbital is in anti phase by one of the hydrogen atoms is in anti-phase in the LGO.
4	0.16839	Anti-bonding	2py and LGO 1	Figure 18: Molecular Orbital 4 Borane	This anti bonding orbital is empty and is in anti phase across the 3 hydrogens and in phase about the boron centre
5	-0.06605	Bonding	Boron 2pz	Figure 19: Molecular Orbital 5 Borane	This molecular orbital has a node across the plane of the Borane molecule

Table 12: Molecular orbital data